Question

State and prove theorem of perpendicular axes.

Explanation

Theorem of perpendicular axes : The moment of inertia of a plane lamina about an axis perpendicular to its plance is equal to the sum of its moments of inertia about two mutually perpendicular axes in its plane and through the point of intersection of the perpendicular axis and the lamina.

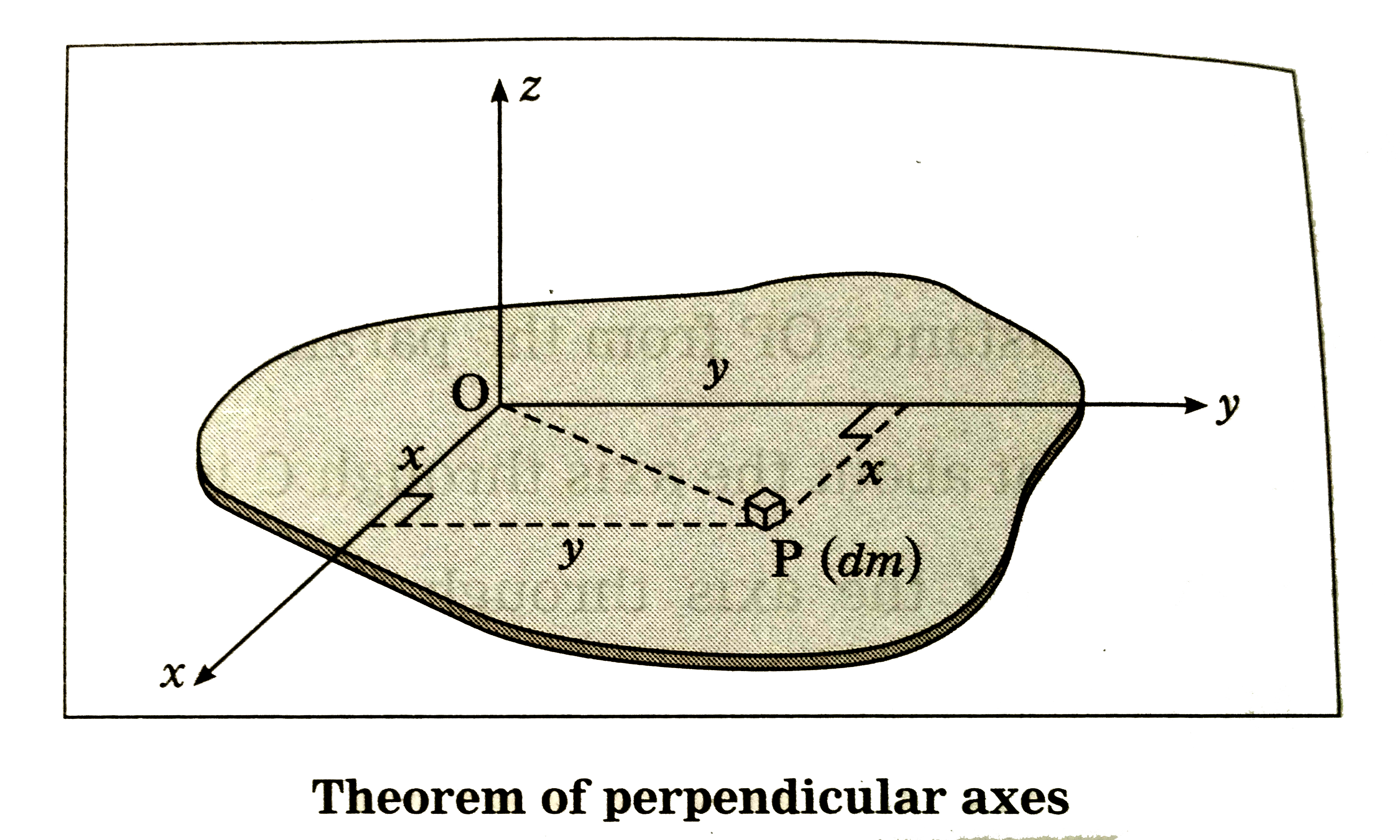
Proof : Let Ox and Oy be two perpendicular axes in the plance of the lamina and Oz, the axis perpendicular to its plane. If `I_(x), I_(y)` and `I_(z)` are the moments of inertia of the lamina about the x,y, and z axes respectively, then, the theorem of perpendicular axes can be stated mathematically as
`I_(z)=I_(x)+I_(y)`.
Consider an infinitesimal volume element of mass dm of the lamina at the point P(x,y). The MI of the lamina about the z-axis is `I_(z)=int OP^(2)` dm. The element is at perpendicular distance y and x from the x- and y-axes respectively. Hence, the moments of inertia of the lamina about the x-and y-axes are respectively `I_(x)= int y^(2) dm `and `I_(y)=int x^(2) dm`.
Since `OP^(2)=y^(2)+x^(2)`,
`I_(z)= int OP^(2) dm =int (y^(2)+x^(2))dm`
`=int y^(2) dm+int x^(2) dm`
`:. I_(z)=I_(x)+I_(y)`
This proves the theorem of perpendicular axes.