State and prove parallel axis theoremSolution in Tamil
Parallel axis theorem. Parallel axis theorem states that the moment of inertia of a body about any axis is equal to the sum of its moment of inertia about a parallel axis through its centre of mass and the product of the mass of the body and the square of the perpendicular distance betwen the two axes.
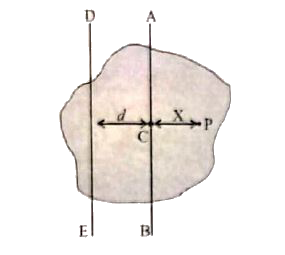
If is the moment of inertia of the body of mass M about an axis passing through the centre of mass, then the moment of inertia I about a parallel axis at a distance d from it is given by:
Let us consider a rigid body as shown in the figure. Its moment of inertia about an axis AB passing thorugh the centre of mass is . Let DE be another axis parallel to AB at a perpendicular distance d from AB. The moment fo inertia of the body about DE is I. Let us attempt to get an express for moment of inertia of the body in tems of . For this, let us consider a point mass m on the body at position x from its centre of mass.
The moment of inertia of the point mass baout the axis DE is .
The summation of the above expression given by the moment of inertia I of the whole body about DE is
Here is the moment of inertia of the body about the centre of mass.
The term , because x can take positive and negative values with respect to the axis AB.
Thus
Here is the entire mass M of the object
Hence, the parallel axis theorem is proved.
Topper's Solved these Questions
- BOOK - PREMIERS PUBLISHERSCHAPTER - MOTION OF SYSTEM OF PARTICLES AND BODIESEXERCISE - TEXTBOOK QUESTIONS & ANSWERS (CONCEPTUAL QUESTIONS)16videos
MOTION OF SYSTEM OF PARTICLES AND BODIES
- BOOK - PREMIERS PUBLISHERSCHAPTER - MOTION OF SYSTEM OF PARTICLES AND BODIESEXERCISE - TEXTBOOK QUESTIONS & ANSWERS (NUMERICAL PROBLEMS)12videos
MOTION OF SYSTEM OF PARTICLES AND BODIES
- BOOK - PREMIERS PUBLISHERSCHAPTER - MOTION OF SYSTEM OF PARTICLES AND BODIESEXERCISE - TEXTBOOK QUESTIONS & ANSWERS (SHORT ANSWER QUESTIONS)34videos
MOTION OF SYSTEM OF PARTICLES AND BODIES
- BOOK - PREMIERS PUBLISHERSCHAPTER - LAW OF MOTION EXERCISE - OTHER IMPORTANT QUESTIONS & ANSWERS (VI Numerical Problems)62videos
LAW OF MOTION
- BOOK - PREMIERS PUBLISHERSCHAPTER - NATURE OF PHYSICAL WORLD AND MEASUREMENTEXERCISE - OTHER IMPORTANT QUESTIONS & ANSWERS (III. Short Answer Questions.)24videos
NATURE OF PHYSICAL WORLD AND MEASUREMENT
Similar Questions
When a tree is cut, the cut is made on the side facing the direction in which the tree is required to fall. Why?
06:58View SolutionA uniform disc of mass 100 g has a diameter of 10 cm. Calculate the total energy of the disc when rolling along a horizontal table with a velocity of 20 cm s−1. (take the surface of table as reference).
06:58View SolutionDefine the center of mass of a body.
View SolutionA scooterist moving with a speed of 36mkmh−1 sees a child standing in the middle of the raod he applies the brakes and brings the scooter to rest in 5s just in time to saved child calculate the average retarding force on the vehicle if mass of the vehicle and drive is 300 kg
04:44View SolutionWhat is meant by Parallax?
04:44View SolutionState and prove theorem of parallel axes.
02:44View SolutionState and prove theorem of parallel axes.
06:45View SolutionState and prove parallel axis theorem.
05:38View SolutionState and prove parallel axis theorem
04:44View SolutionState and prove parallel axis theorem
04:44View SolutionState the theorem of parallel axis.
05:38View SolutionState and explain parallel axis theorem and perpendicular axis theorem.
04:44View SolutionState and prove perpendicular axis theorem.
04:44View SolutionState and prove parallel axis theorem
03:10View SolutionState and prove parallel axis theorem
08:03View Solution
