State and prove prism formula.

Video Solution

Text Solution

Verified by Experts

Refraction. The phenomenon of change in path of a ray of light as it passes from one medium into another is called refraction.
Let a ray DE strikes the face AB of the prism at an angle of incidence i and emerges out at an angle e. Let $r_{1}$ and $r_{2}$ be the angles of refraction and $δ$ be exterior angle of deviation.
$δ$ is exterior angle of triangle HEF
$∴ δ = 1 + 2 = (i - r_{1}) + (e - r_{2})$
or $δ = i + e - (r_{1} + r_{2})$ ...(1)
In quadrilateral AEOF, we have
$∠ A E O + A + ∠ A F O + ∠ O = 360^{\circ}$
or $90^{\circ} + A + 90^{\circ} + ∠ O = 360^{\circ}$
or $A + ∠ O = 180^{\circ}$

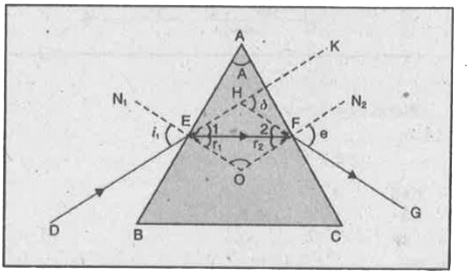
Also, in triangle FEO,
$r_{1} + r_{2} + ∠ O = 180^{\circ}$
$A + ∠ O = r_{1} + r_{2} + ∠ O$
or $A = r_{1} + r_{2}$ ...(ii)
Substituting in equation (i), we have
$δ = i + e - A$
or $A + δ = i + e$
For small angled prism,
At face AB,
$\frac{sin i}{{sin r}_{1}} = \frac{i}{r_{1}} = (μ)$
or $i = μ r_{1}$
Similarly, at face AC,
$e = μ r_{2}$
Putting the value of i and e in equation (iii), we get
$δ = μ r_{1} + μ r_{2} - A = μ (r_{1} + r_{2}) - A$
Using equation (ii), we get
$δ = (μ - 1) A$ ...(iv)
If we repeat the experiment with different angles of incidence, then we get a graph as shown in the figure when i is increased, $δ$ decreases first, reaches a minimum and starts increasing again. For a particular value of $δ$ , there are two angles of incidence $i_{1}$ and $i_{2}$ , At minimum deviation,

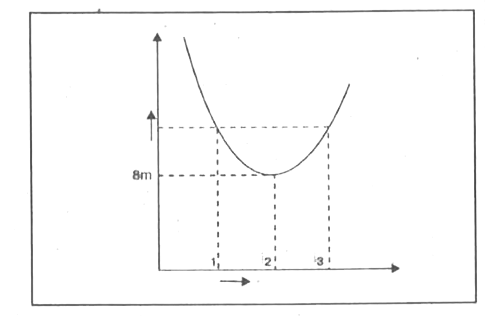
$δ = δ_{m}$ and $i_{1} = i_{2} = i$
Hence $r_{1} = r_{2} = r$
$∴ r + r = 2 A$ or $r = \frac{A}{2}$
And $δ_{m} = i + i - A$
or $2 i = A + δ_{m}$
or $i = \frac{A + δ_{m}}{2}$
Now $μ = \frac{sin i}{sin r} = \frac{\frac{sin (A + δ_{m})}{2}}{\frac{sin (A)}{2}}$

|

Class 12 PHYSICS GEOMETRICAL OPTICS

Topper's Solved these Questions

Similar Questions

MBD -HARYANA BOARD-OPTICS-LONG ANSWER TYPE QUESTIONS

Home
Ask Doubt
Profile