STATEMENT-1 : In simple pendulum performing S.H.M., net acceleration is always between tangential and radial acceleration except at lowest point.
STATEMETN-2 : At lowest point tangential acceleration is zero.
(a)Statement I is true statement II is true, Statement II is a correct explanation for Statement I.
(b)Statement I is true statement II is true, Statement II is NOT a correct explanation for Statement I.
(c)Statement I is true, Statement II is false
(d)Statement I is false, Statement II is true
The correct Answer is:D
To solve the problem, we need to analyze both statements given in the question regarding the simple harmonic motion (SHM) of a simple pendulum.
Step 1: Understanding Statement 1
- Statement 1 claims that in a simple pendulum performing SHM, the net acceleration is always between the tangential and radial (centripetal) acceleration except at the lowest point.
- In SHM, the pendulum experiences two components of acceleration:
- Tangential Acceleration (a_t): This is due to the component of gravitational force acting along the direction of motion (mg sin θ).
- Radial Acceleration (a_r): This is due to the tension in the string and the component of gravitational force acting perpendicular to the direction of motion (mg cos θ).
- The net acceleration (a_net) is a vector sum of these two components. At any point other than the lowest point, the net acceleration will indeed lie between these two components.
Conclusion for Statement 1: True.
Step 2: Understanding Statement 2
- Statement 2 states that at the lowest point, the tangential acceleration is zero.
- At the lowest point of the pendulum's swing (when θ = 0), the motion is purely horizontal, and the gravitational force acts vertically downward.
- Since tangential acceleration is given by a_t = g sin θ, at θ = 0, sin(0) = 0, which means:
- Tangential Acceleration (a_t) = 0.
Conclusion for Statement 2: True.
Step 3: Evaluating the Relationship Between the Statements
- Both statements are true, but they describe different aspects of the motion of the pendulum.
- Statement 1 discusses the relationship between net acceleration and its components throughout the motion, while Statement 2 specifically addresses the condition at the lowest point.
Final Conclusion:
Both Statement 1 and Statement 2 are true, but they are not directly explaining each other. Therefore, the correct answer is that both statements are true, but Statement 2 does not provide a correct explanation for Statement 1.
Answer: Option B (Both statements are true, but Statement 2 is not a correct explanation for Statement 1).
---
- Statement 1 claims that in a simple pendulum performing SHM, the net acceleration is always between the tangential and radial (centripetal) acceleration except at the lowest point.
- In SHM, the pendulum experiences two components of acceleration:
- Tangential Acceleration (a_t): This is due to the component of gravitational force acting along the direction of motion (mg sin θ).
- Radial Acceleration (a_r): This is due to the tension in the string and the component of gravitational force acting perpendicular to the direction of motion (mg cos θ).
- The net acceleration (a_net) is a vector sum of these two components. At any point other than the lowest point, the net acceleration will indeed lie between these two components.
- Statement 2 states that at the lowest point, the tangential acceleration is zero.
- At the lowest point of the pendulum's swing (when θ = 0), the motion is purely horizontal, and the gravitational force acts vertically downward.
- Since tangential acceleration is given by a_t = g sin θ, at θ = 0, sin(0) = 0, which means:
- Tangential Acceleration (a_t) = 0.
Conclusion for Statement 2: True.
- Both statements are true, but they describe different aspects of the motion of the pendulum.
- Statement 1 discusses the relationship between net acceleration and its components throughout the motion, while Statement 2 specifically addresses the condition at the lowest point.
Both Statement 1 and Statement 2 are true, but they are not directly explaining each other. Therefore, the correct answer is that both statements are true, but Statement 2 does not provide a correct explanation for Statement 1.
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Comprehension
33 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Integer
10 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct
35 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
In a typical projectile motion, tangential acceleration at the topmost point P of the trajectory is
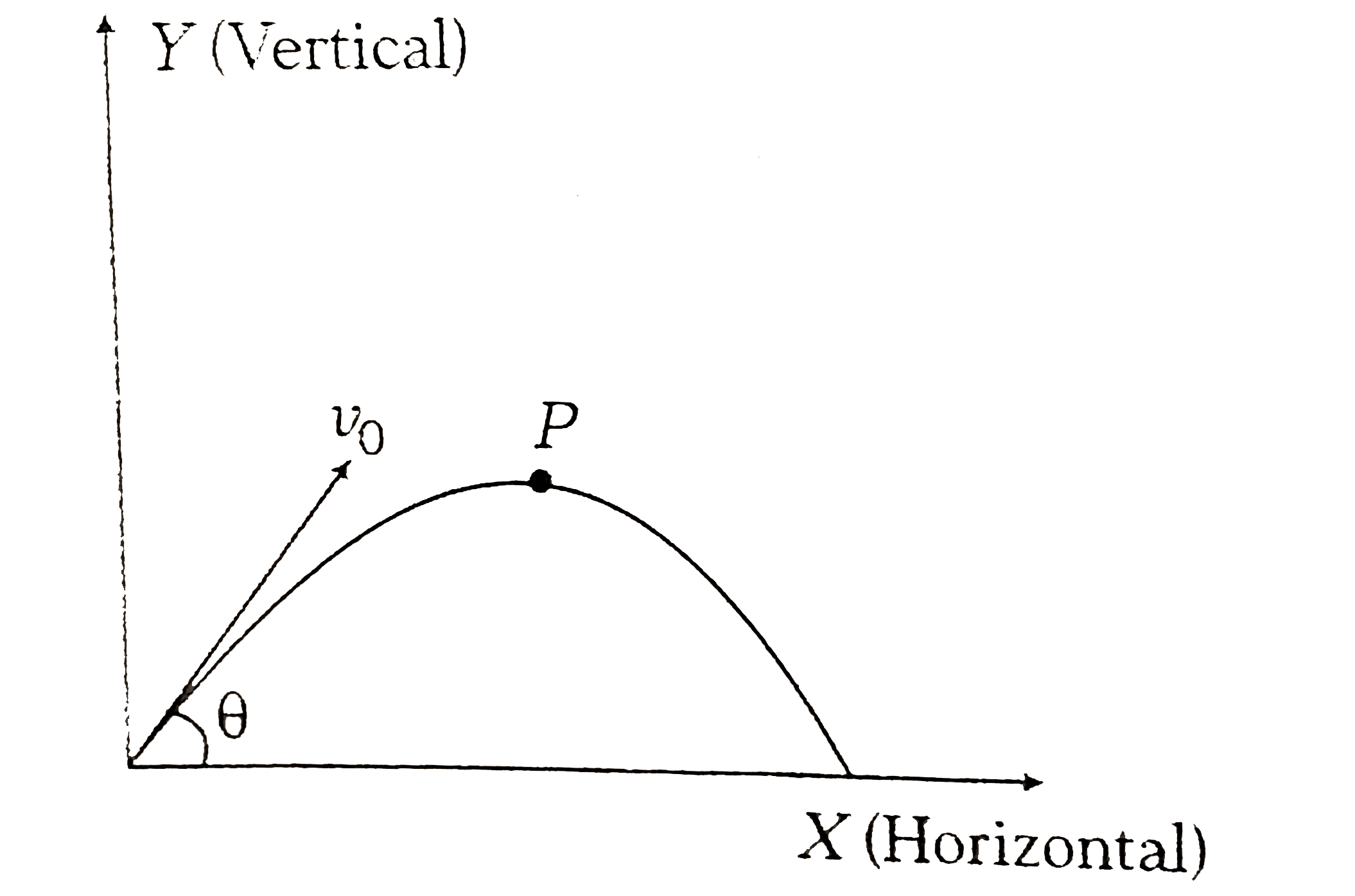
View SolutionA point starts from rest and moves along a circular path with a constant tangential acceleration. After one rotation, the ratio of its radial acceleration to its tangential acceleration will be equal to
View Solution
Knowledge Check
Consider the following statements in relation to the motion of a simple pendulum :
(1) The acceleration is always directed towards the mean position
(2) the maximum acceleration occurs at the mean position
(3) The maximum velocity occurs at the mean position
(4) The magnitude of maximum acceleration is equal to the maximum velocity
Which of the following statements are correct ?A1 and 2B1 and 3C3 and 4D2 and 4
A point mass moves along a circle of radius R with a constant angular acceleration α. How much time is needed after motion begins for the radial acceleration of the point mass to be equal to its tangential acceleration ?
View SolutionSTATEMENT -1 : If a simple pendulum is in a carriage which is accelerating downward and acceleration is greater than acceleration due to gravity , then pendulum turns up side down and oscillates about highest point.
and
STATEMENT -2 : The time period of pendulum will be independent of g in above case of pendulum oscillating about highest point.
View SolutionAssertion: A pendulam is oscillating between points A , B and C . Acceleration of bob at points A or C is zero.
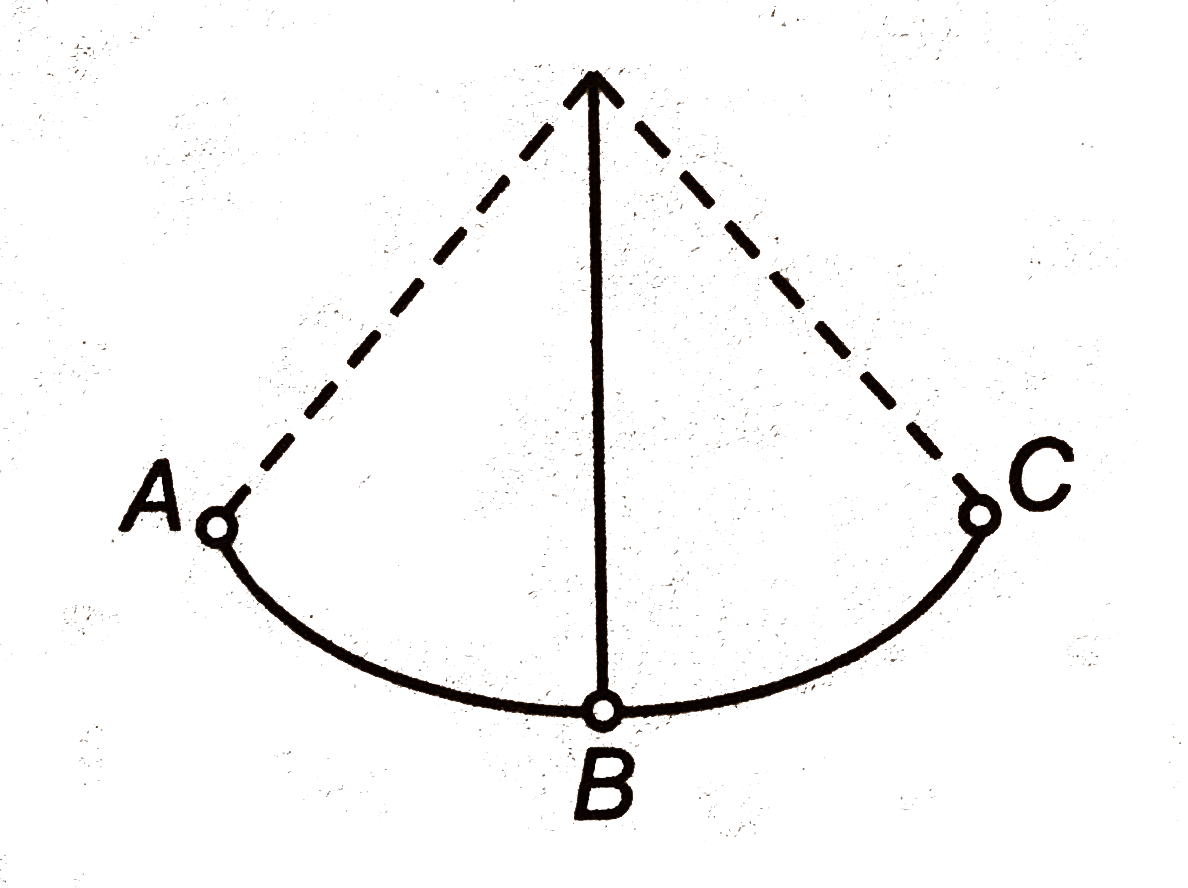
Reason: Velocity at these points is zero.
View SolutionA particle moves in a circle with constant tangential acceleration starting from rest. At t = 1/2 s radial acceleration has a value 25% of tangential acceleration. The value of tangential acceleration will be correctly represented by
View SolutionIn the following questions a statement of assertion (A) is followed by a statement of reason ( R).
A: When a body moves on a curved path with increasing speed then angle between instantaneous velocity and acceleration is acute angle.
R: When the speed is increasing its tangential acceleration is in the direction of instaneous velocity .
View SolutionOne end of massless inextensible string of length l is fixed and other end is tied to a small ball of mass m. The ball is performing a circular motion in vertical plane. At the lowest position, speed of ball is √20gl. Neglect any other forces on the ball except tension and gravitational force. Acceleration due to gravity is g.
At the highest position of ball, tangential acceleration of ball is −
View SolutionA particle is moving along a circle and its linear velocity is 0.5ms when its angular velocity is 2.5rads−1. Its tangential acceleration is 0.2ms−2 then its angular acceleration is
View Solution
