Statement I: A block is lying stationary as on inclined plane and coefficient of friction is μ. Friction on block is μmgcosθ.

Statement II: Contact force on block is mg.
Statement I is true, statement II is true, Statement II is the correct explanation for statement I.
Statemet I is true, Statement II is true , Statement II is NOT the correct explanation for Statement I
Statement I is True, Statement II is False.
Statement I is False, Statement II is true
The correct Answer is:D
Contact force is the sum of friction and normal reaction.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Linked Comperhension
46 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Multiple Correct
11 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
Similar Questions
The coefficient of friction between the block and the inclined plane is μ.
View SolutionA block of mass m is placed over rough inclined plane having inclination 30∘ .The co-efficient of friction between the block and inclined plane is 0.75.The contact force on the block is x4mg. Find the value of x
View Solution
Knowledge Check
A block is stationary on an inclined plane If the coefficient of friction between the block and the plane is μ then
 .Aμ>tanθBf=mgsinθCf=μmgcosθDthe reaction of the ground on the block is mg cos θ
.Aμ>tanθBf=mgsinθCf=μmgcosθDthe reaction of the ground on the block is mg cos θA block of mass mm remains stationary on a fixed inclined plane of inclination θ . If μ= coefficient of static friction the reaction of ground on the block is:
AμgcosθBmgcosθCmgsinθDmg↓A block of mass m is lying on an inclined plane. The coefficient of friction between the plane and the block is μ. The force (F1) required to move the block up the inclined plane will be:-
Amgsinθ+μmgcosθBmgcosθ−μmgsinθCmgsinθ−μmgcosθDmgcosθ+μmgsinθ
A block of mass m is at rest on a rough inclined plane, whose friction coefficient is μ. Net force exerted by surface on block is :-
View SolutionA block of mass M is sliding down the plane. Coefficient of static friction is μs and kinetic friction is μk. Then friction force acting on the block is :
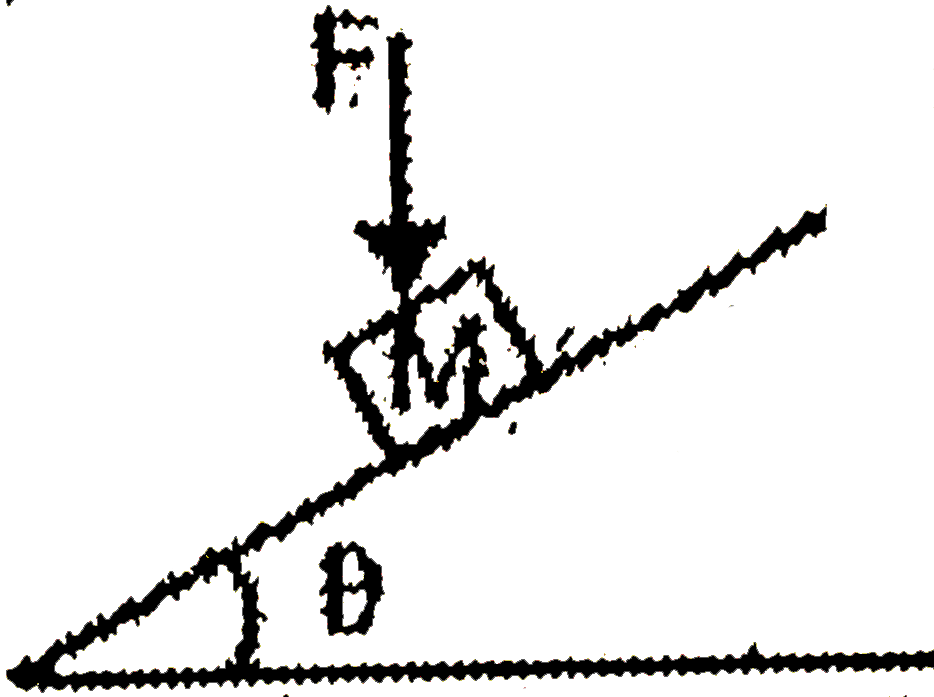
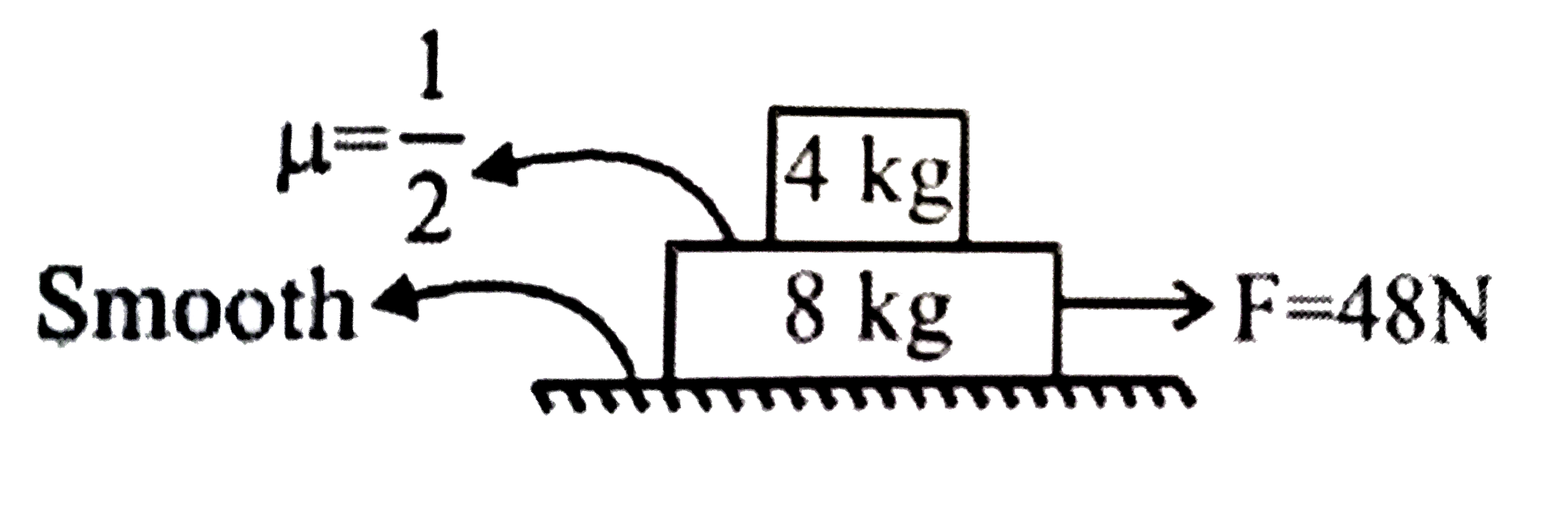
View SolutionIf coefficient of friction between both the block is μ−12 . Find friction force acting between both block.
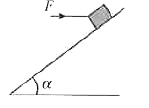
View SolutionA block of mass m in the equilib rium on a rough inclined plane with inclination α and coefficient of friction as shown in the figure (μ<tanα). A force F is applied on the block which makes an angle θ with the horizontal as shown in diagram.
View SolutionA block is placed on an inclined plane. The angle of inclination of the plane is such that the block slides down the plane at a constant speed. The coefficient of kinetic friction is
View Solution
