Statement I: A circular metal hop is suspended on the edge by a hook. the hoop can oscillate side to side in the plane of the hoop, or it can oscillate back and forth in a direction perpendicular to the plane of the hoop. The time period of oscillation would be more when oscillation are carried out in the plane of hoop.
Statement II: Time period of physical pendulum is more if moment of inertial of the rigid body about corresponding axis passing through the pivoted point is more.
(a)Statement I is true statement II is true, Statement II is a correct explanation for Statement I.
(b)Statement I is true statement II is true, Statement II is NOT a correct explanation for Statement I.
(c)Statement I is true, Statement II is false
(d)Statement I is false, Statement II is true
The correct Answer is:A
To solve the problem, we need to analyze both statements regarding the oscillation of a circular metal hoop and the relationship between the moment of inertia and the time period of oscillation.
1. Understanding the Setup:
- A circular metal hoop is suspended at its edge by a hook.
- The hoop can oscillate in two different ways:
- Side to side in the plane of the hoop.
- Back and forth in a direction perpendicular to the plane of the hoop.
2. Time Period of Oscillation:
- The time period T of a physical pendulum is given by the formula:
T=2π√Imgd
where:
- I is the moment of inertia about the pivot point,
- m is the mass of the hoop,
- g is the acceleration due to gravity,
- d is the distance from the pivot to the center of mass.
3. Calculating Moment of Inertia:
- For a circular hoop of mass m and radius R:
- When oscillating in the plane of the hoop (let's denote this as I1), the moment of inertia about the pivot point (edge of the hoop) can be calculated using the parallel axis theorem:
I1=ICM+md2=12mR2+mR2=32mR2
- When oscillating perpendicular to the plane of the hoop (let's denote this as I2):
I2=ICM+md2=12mR2+mR2=2mR2
4. Comparing Time Periods:
- The time period for oscillation in the plane of the hoop (using I1):
T1=2π√I1mgd=2π
⎷32mR2mgR=2π√3R2g
- The time period for oscillation perpendicular to the plane of the hoop (using I2):
T2=2π√I2mgd=2π√2mR2mgR=2π√2Rg
5. Conclusion:
- Since T1 involves √3R2g and T2 involves √2Rg, we can see that T1>T2.
- Therefore, the time period of oscillation is greater when the oscillation is carried out in the plane of the hoop.
Evaluation of Statements:
- Statement I: True. The time period of oscillation is more when oscillations are carried out in the plane of the hoop.
- Statement II: True. The time period of a physical pendulum is more if the moment of inertia about the corresponding axis passing through the pivot point is greater.
Thus, both statements are correct.
- A circular metal hoop is suspended at its edge by a hook.
- The hoop can oscillate in two different ways:
- Side to side in the plane of the hoop.
- Back and forth in a direction perpendicular to the plane of the hoop.
- The time period T of a physical pendulum is given by the formula:
T=2π√Imgd
where:
- I is the moment of inertia about the pivot point,
- m is the mass of the hoop,
- g is the acceleration due to gravity,
- d is the distance from the pivot to the center of mass.
- For a circular hoop of mass m and radius R:
- When oscillating in the plane of the hoop (let's denote this as I1), the moment of inertia about the pivot point (edge of the hoop) can be calculated using the parallel axis theorem:
I1=ICM+md2=12mR2+mR2=32mR2
- When oscillating perpendicular to the plane of the hoop (let's denote this as I2):
I2=ICM+md2=12mR2+mR2=2mR2
- The time period for oscillation in the plane of the hoop (using I1):
T1=2π√I1mgd=2π
⎷32mR2mgR=2π√3R2g
- The time period for oscillation perpendicular to the plane of the hoop (using I2):
T2=2π√I2mgd=2π√2mR2mgR=2π√2Rg
- Since T1 involves √3R2g and T2 involves √2Rg, we can see that T1>T2.
- Therefore, the time period of oscillation is greater when the oscillation is carried out in the plane of the hoop.
- Statement I: True. The time period of oscillation is more when oscillations are carried out in the plane of the hoop.
- Statement II: True. The time period of a physical pendulum is more if the moment of inertia about the corresponding axis passing through the pivot point is greater.
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Comprehension
33 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Integer
10 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct
35 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
The time period of small oscillations of mass m :-
_S01_040_Q01.png)
View SolutionThe time period of oscillation of the block as shown in figure is
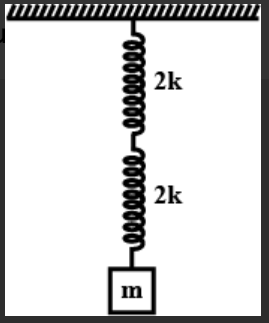
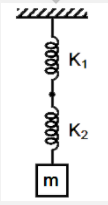
View SolutionTime period of oscillation for given combination will be :
View SolutionA ring is hung on a nail. It can oscillate without slipping or sliding (i) in its plane with a time period T1 and (ii) , back and forth in a direction perpendicular to its plane , with a period T2. The ratio T1T2 will be :
View SolutionWhat is a torsional pendulum ? Name the factors on which its period of oscillation depends ?
View SolutionA small block oscillates back and forth on as smooth concave surface of radius R in figure. Find the time period of small oscillation.

View SolutionThe time period of oscillation of a freely suspended bar magnet with usual notations is given by
View SolutionA seconds pendulum is mounted in a rocket. Its period of oscillation decreases when the rocket
View SolutionThe period of oscillations of a magnet is 2 sec. When it is remagnetised so that the pole strength is 4 times its period will be
View SolutionThe period of oscillations of a magnet is 2 sec. When it is remagnetised so that the pole strength is 4 times its period will be
View Solution
