Suppose a smooth tunnel is dug along a straight line joining two points on the surface of the earth and a particle is dropped from rest at its one end. Assume that mass of earth is uniformly distributed over its volume. Then
The particle will emerge from the other end with velocity GMe2Re, where Me and Re are earth's mass and radius, respectively.
The particle will come to rest at the centre of the tunnel because at this position, the particle is closest to the earth's centre.
Potential energy of the particle will be equal to zero at centre of the tunnel if it is along a diameter.
Acceleration of the particle will be proportional to its distance from the mid-point of the tunnel.
The correct Answer is:A, B, C
When the particle is dropped in the tunnel at its one end, it starts to execute simple harmonic motion with mean position as the centre of the tunnel. Hence, acceleration of the particle is directly proportional to its distance from he centre of the tunnel. It means option d is correct.
The particle has zero velocity at one end because it is dropped from rest at that end, therefore ends of the tunnel are its extreme positions. Hence at the other end, the velocity will extreme positions. Hence at the other end, the velocity will become equal to zero. It means optioin a is incorrect.
Velocity of a particle executing S.H.M. is maximum at its mean position. Hence at the centre of the tunnel, its velocity will be maximum possible. Hence, option b is incorrect.
When the particle moves from extreme position to centre of the tunel, its velocity increases. It means KE increases or PE decreases. But initial potential energy becomes more negative and it is least at the mid-point of the tunnel because KE is maximum there. It means the gravitational PE can never be equal to zero. Hence, option c is also incorrect.
Topper's Solved these Questions
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Assertion- Reasoning
13 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Linked Comprehension
23 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Single Correct
122 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE
1 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
Similar Questions
Suppose a smooth tunnel is dug along a straight line joining two points on the surface of the earth and a particle is dropped from rest at its one end. Assume that mass of the earth is uniformly distributed over its volume. Then, which of the following statements are not correct?
View SolutionSuppose a tunnel is dug along a diameter of the earth. A particle is dropped from a point at a distance h directly above the tunnel. The motion of the particle as seen from the earth is
View SolutionA tunnel is dug along a diameter of the earth. Find the force in on a particle of mass m placed in the tunnel at a distance x from the centre.
View SolutionA hole is drilled from the surface of earth to its centre. A particle is dropped from rest in the surface of earth in terms of its escape velocity on the surface of earth ve is :
View SolutionA particle of mass m is dropped from a great height h above the hole in the earth dug along its diameter.
View SolutionIf a smooth tunnel is dug across a diameter of earth and a particle is released from the surface of earth, the particle oscillate simple harmonically along it
Maximum speed of the particle is
View Solutiona narrow tunnel is dug along the diameter of the earth, and a particle of mass m0 is placed at R2 distance from the centre. Find the escape speed of the particle from that place.

View SolutionThe acceleration versus time graph for a particle moving along a straight line is shown in the figure. If the particle starts from rest at t = 0, then its speed at t = 30 sec will be :
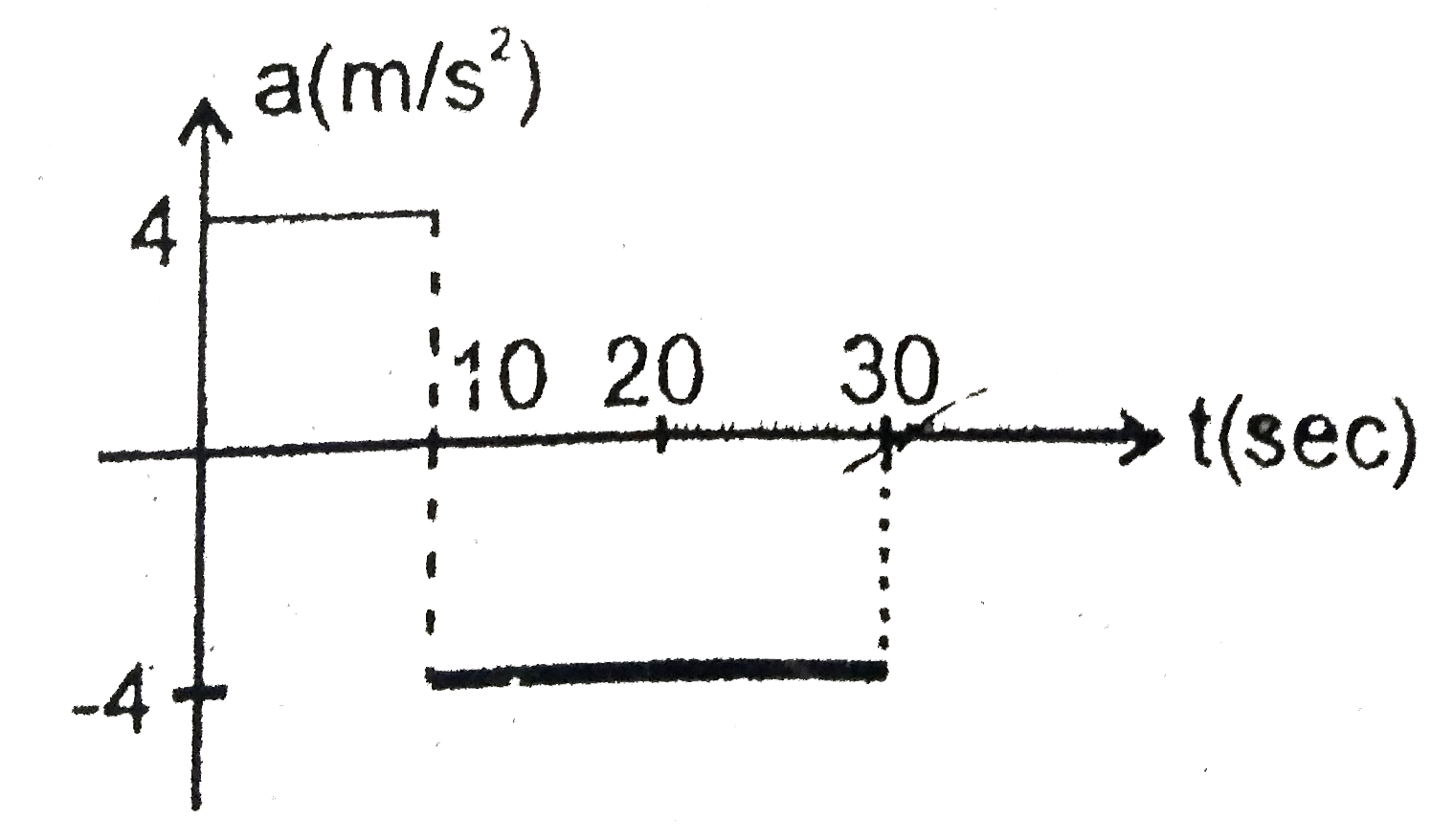
View SolutionIf a smooth tunnel is dug across a diameter of earth and a particle is released from the surface of earth, the particle oscillate simple harmonically along it
Time period of the particle is not equal to
View SolutionConsider the earth as a uniform sphere if mass M and radius R. Imagine a straight smooth tunnel made through the earth which connects any two points on its surface. Show that the motion of a particle of mass m along this tunnel under the action of gravitation would be simple harmonic. Hence, determine the time that a particle would take to go from one end to the other through the tunnel.
View Solution
