Suppose a smooth tunnel is dug along a straight line joining two points on the surface of the earth and a particle is dropped from rest at its one end. Assume that mass of the earth is uniformly distributed over its volume. Then, which of the following statements are not correct?
the particle will emerge from the other end will velocity √GMe2Re, where MeandRe are earth's mass and radius respectively
the overlapping will come to rest at centre of the tunnel
potential energy of the particle will be equal to zero at centre of tunnel if it is along a diameter
acceleration of the particle will be proportional to its distance from mid-point of the tunnel
The correct Answer is:D
To solve the problem, we need to analyze the statements provided regarding a particle dropped in a smooth tunnel dug through the Earth. We assume that the mass of the Earth is uniformly distributed. Let's evaluate each statement step by step.
Step 1: Understanding the Motion of the Particle
When a particle is dropped into a tunnel that goes through the Earth, it will experience gravitational force. As it falls towards the center, the gravitational force acting on it will change due to the uniform distribution of mass.
Step 2: Statement Analysis
1. Statement A: "The particle will emerge from the other end with a velocity of √gMe2Re."
- Analysis: This statement is correct. The particle will convert its potential energy at the starting point into kinetic energy as it falls, and it will reach the other end with the same speed it had at the starting point due to conservation of energy.
2. Statement B: "The particle will come to rest at the center of the tunnel."
- Analysis: This statement is incorrect. The particle will not come to rest at the center; instead, it will continue to oscillate back and forth through the tunnel due to the restoring force of gravity acting on it.
3. Statement C: "The potential energy of the particle will be equal to zero at the center of the tunnel if it is along a diameter."
- Analysis: This statement is incorrect. The potential energy is not zero at the center; it is at a minimum. The potential energy is defined relative to a reference point, and it reaches its minimum value at the center of the Earth.
4. Statement D: "The acceleration of the particle will be proportional to its distance from the midpoint of the tunnel."
- Analysis: This statement is correct. According to Hooke's Law, the gravitational force (and thus the acceleration) acting on the particle is proportional to its distance from the center of the Earth (or midpoint of the tunnel).
Conclusion
From the analysis:
- Correct Statements: A and D
- Incorrect Statements: B and C
Thus, the statements that are not correct are B and C.
Final Answer
The statements that are not correct are:
- Statement B: "The particle will come to rest at the center of the tunnel."
- Statement C: "The potential energy of the particle will be equal to zero at the center of the tunnel if it is along a diameter."
When a particle is dropped into a tunnel that goes through the Earth, it will experience gravitational force. As it falls towards the center, the gravitational force acting on it will change due to the uniform distribution of mass.
1. Statement A: "The particle will emerge from the other end with a velocity of √gMe2Re."
- Analysis: This statement is correct. The particle will convert its potential energy at the starting point into kinetic energy as it falls, and it will reach the other end with the same speed it had at the starting point due to conservation of energy.
- Analysis: This statement is incorrect. The particle will not come to rest at the center; instead, it will continue to oscillate back and forth through the tunnel due to the restoring force of gravity acting on it.
- Analysis: This statement is incorrect. The potential energy is not zero at the center; it is at a minimum. The potential energy is defined relative to a reference point, and it reaches its minimum value at the center of the Earth.
- Analysis: This statement is correct. According to Hooke's Law, the gravitational force (and thus the acceleration) acting on the particle is proportional to its distance from the center of the Earth (or midpoint of the tunnel).
From the analysis:
- Correct Statements: A and D
- Incorrect Statements: B and C
The statements that are not correct are:
- Statement B: "The particle will come to rest at the center of the tunnel."
- Statement C: "The potential energy of the particle will be equal to zero at the center of the tunnel if it is along a diameter."
Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (B) Chapter Exercises
31 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Check Point 10.6
20 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
10 Videos
Similar Questions
Suppose a tunnel is dug along a diameter of the earth. A particle is dropped from a point at a distance h directly above the tunnel. The motion of the particle as seen from the earth is
View SolutionA uniform plank is resting over a smooth horizontal floor and is pulled by applying a horizontal force at its one end. Which of the following statements are not correct?
View SolutionA uniform plank is resting over a smooth horizontal floor and is pulled by applying a horizontal force at its one end. Which of the following statements are not correct?
View SolutionA hole is drilled from the surface of earth to its centre. A particle is dropped from rest in the surface of earth in terms of its escape velocity on the surface of earth ve is :
View SolutionIf a smooth tunnel is dug across a diameter of earth and a particle is released from the surface of earth, the particle oscillate simple harmonically along it
Maximum speed of the particle is
View SolutionA particle of mass m is dropped from a great height h above the hole in the earth dug along its diameter.
View SolutionFigure shows acceleration versus time graph of a particle starting from rest and moving along a straight line. Which of the following staement (s) is/are correct ?
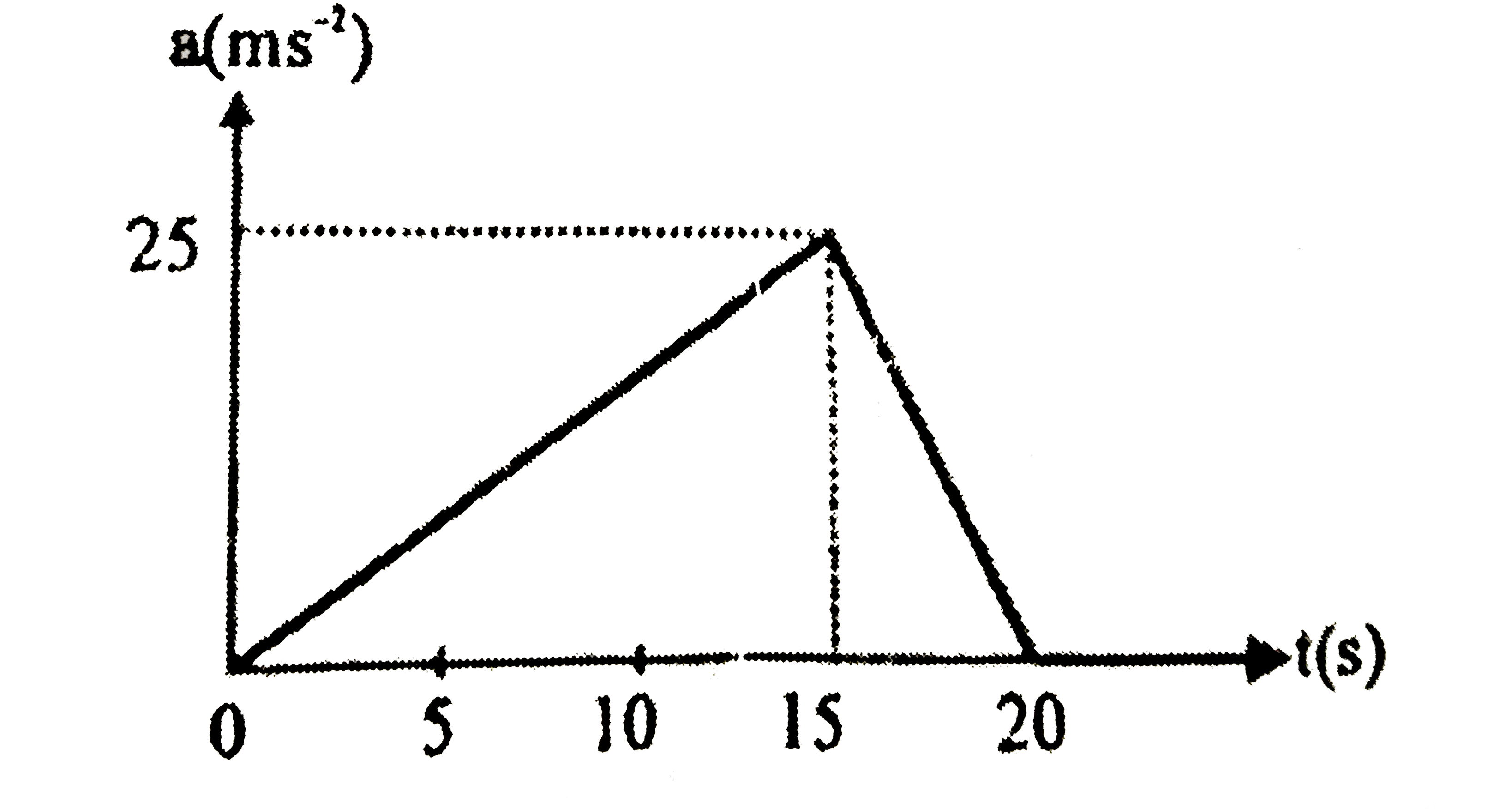
View SolutionIf a smooth tunnel is dug across a diameter of earth and a particle is released from the surface of earth, the particle oscillate simple harmonically along it
Time period of the particle is not equal to
View SolutionTwo spheres of masses mand2m are separated by distance d. A particle of mass m5 is projected straight from 2m towards m with a velocity v0. Which of the following statements is correct ?
View SolutionThe velocity v of a particle of mass is moving along a straight line change with time t as d2vdt2=−Kv where K is a particle constant which of the following statement is correct?
View Solution
