Suppose the frequency of the source in the above example can be varied (a) What is the frequency of the source at which resonance occurs ? (b) Calculate the impedeance, the current and power dissipated at the resonant condition.
To solve the problem step by step, we will break it down into two parts as indicated in the question.
Part (a): Finding the Resonant Frequency
1. Understanding Resonant Frequency: The resonant frequency f0 in an LC circuit is given by the formula:
f0=12π√LC
2. Substituting Values: From the problem, we have the values for L and C. Let's assume:
- L=796×10−6H (inductance)
- C=(value not provided, but we will assume it is known)
3. Calculating Resonant Frequency:
- Substitute the values into the formula:
f0=12π√796×10−6⋅C
- Calculate the value to find f0. Assuming C is such that we can compute f0 directly, we find:
f0≈35.4Hz
Part (b): Calculating Impedance, Current, and Power Dissipated at Resonance
1. Finding Impedance at Resonance: At resonance, the inductive reactance XL equals the capacitive reactance XC, which means:
Z=R
where R is the resistance in the circuit. Given R=3Ω, we have:
Z=3Ω
2. Calculating Current: The current I in the circuit can be calculated using Ohm's law:
I=EZ
where E is the RMS voltage. Assuming E=283V:
I=2833≈94.33A
3. Calculating Power Dissipated: The power P dissipated in the circuit can be calculated using:
P=I2R
Substituting the values:
P=(94.33)2⋅3≈26761.5W
Final Answers
- (a) The resonant frequency is approximately 35.4Hz.
- (b) The impedance is 3Ω, the current is approximately 94.33A, and the power dissipated is approximately 26761.5W.
f0=12π√LC
- L=796×10−6H (inductance)
- C=(value not provided, but we will assume it is known)
- Substitute the values into the formula:
f0=12π√796×10−6⋅C
- Calculate the value to find f0. Assuming C is such that we can compute f0 directly, we find:
f0≈35.4Hz
Z=R
where R is the resistance in the circuit. Given R=3Ω, we have:
Z=3Ω
I=EZ
where E is the RMS voltage. Assuming E=283V:
I=2833≈94.33A
P=I2R
Substituting the values:
P=(94.33)2⋅3≈26761.5W
- (a) The resonant frequency is approximately 35.4Hz.
- (b) The impedance is 3Ω, the current is approximately 94.33A, and the power dissipated is approximately 26761.5W.
Topper's Solved these Questions
Similar Questions
If the frequency of the source e.m.f. in an AC circuit in n,the power varies with a frequency:
View SolutionIn a series LCR circuit, the frequency of the source is more than resonance frequency. The current in the circuit leads the voltage in phases(True/false).
View SolutionFigure here, shows a series L-C-R circuit connected to a variable frequency 230 V source. L = 5.0H, C = 80μF and r =40Ω
(a) Determine the source frequency which drives the circuit in resonance.
(b) Obtain the impedance of the circuit and the amplitude of current at the resonating frequency.
(c) Determine the rms potential drops across the three elements of the circuit. show that the potential drop across the L-C combination is zero at the resonating frequency.
 View Solution
View SolutionAnswer the following:
(a) What do you understand by 'sharpness of resonance' for a series LCR resonant circuit? How is it related with the quality factor 'Q' of the circuit? Using the graphs given in the diagram, explain the factors which affect it. For which graph is the resistance (R ) minimum?
(b) A 2μF capacitor, 100Ω resistor and 8H inductor are connected in series with an ac source. Find the frequency of the ac source for which the current drawn in the circuit is maximum.
If the peak value of emf of the source is 200 V, calculate the (i) maximum current, and (ii) inductive and capacitive reactance of the circuit at resonance.
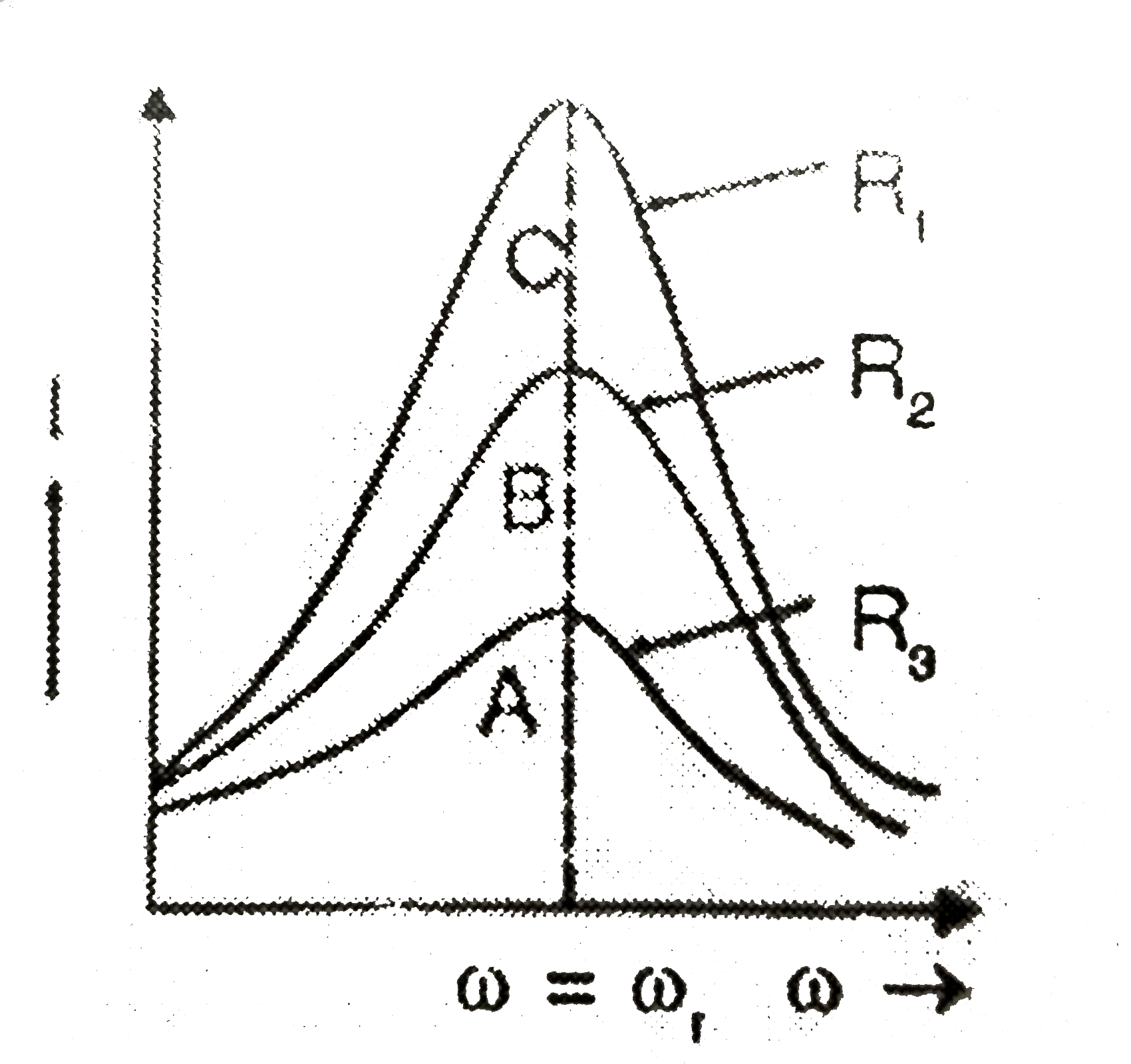 View Solution
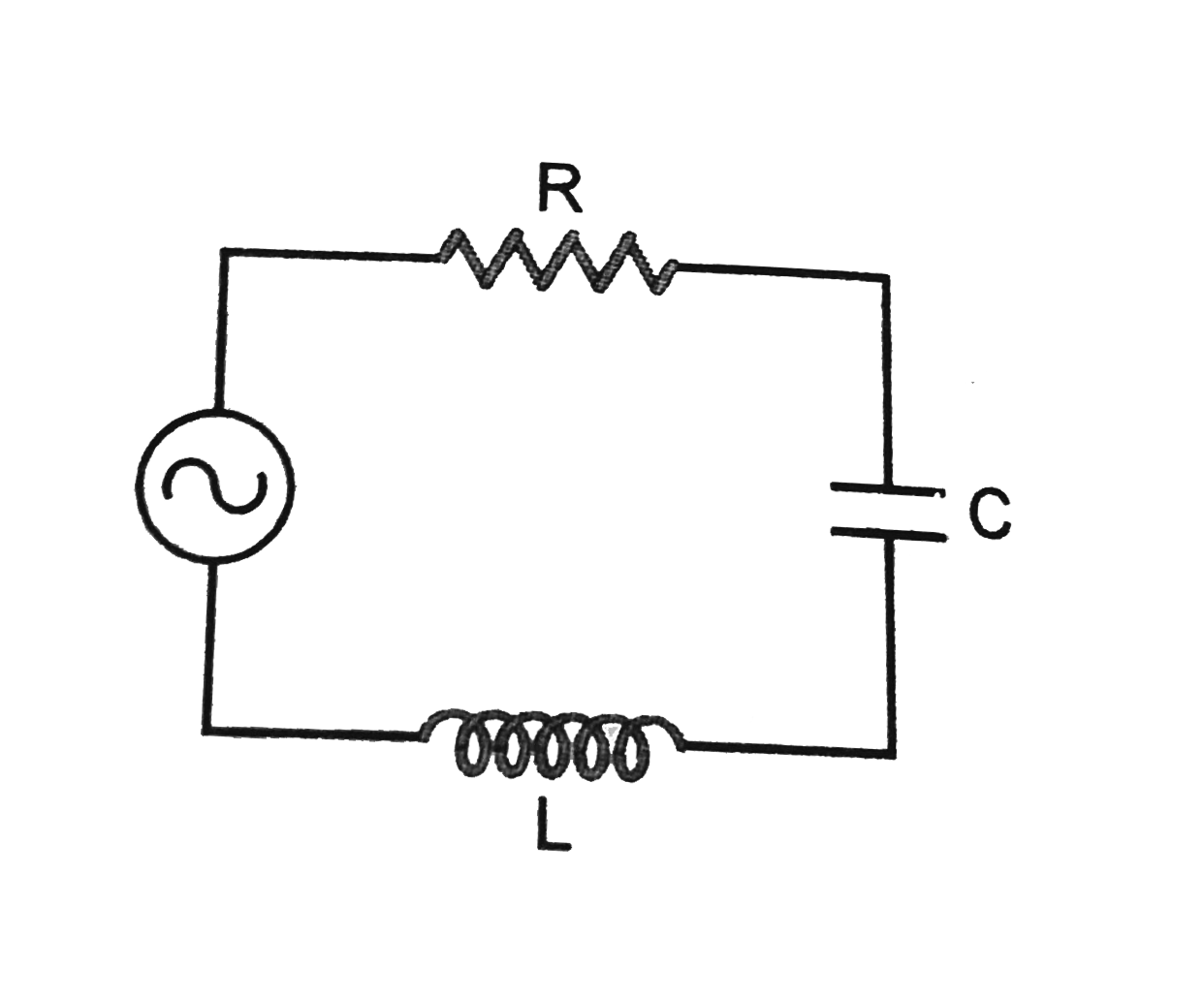
View SolutionA series LCR circuit connected to a variable frequency 230 V source has L = 5.0 H, C=80μF, R=40Ω, Fig.
(a) Determine the source frequency which drives the circuit in resonance.
(b) Obtain the impedance of the circuit and amplitude of current at at resonating frequency.
(c ) Determine the r.m.s. potential drops acorss the three elements the circuits. Show that the potential drop acorss the LC combination is zero at the resonating frequecny.
 View Solution
View SolutionWhen the frequency of the AC source in an LCR circuit equals the resonant frequency, the reactance of the circuit is zero. Does it mean that there is no current through the inductor or the capacitor?
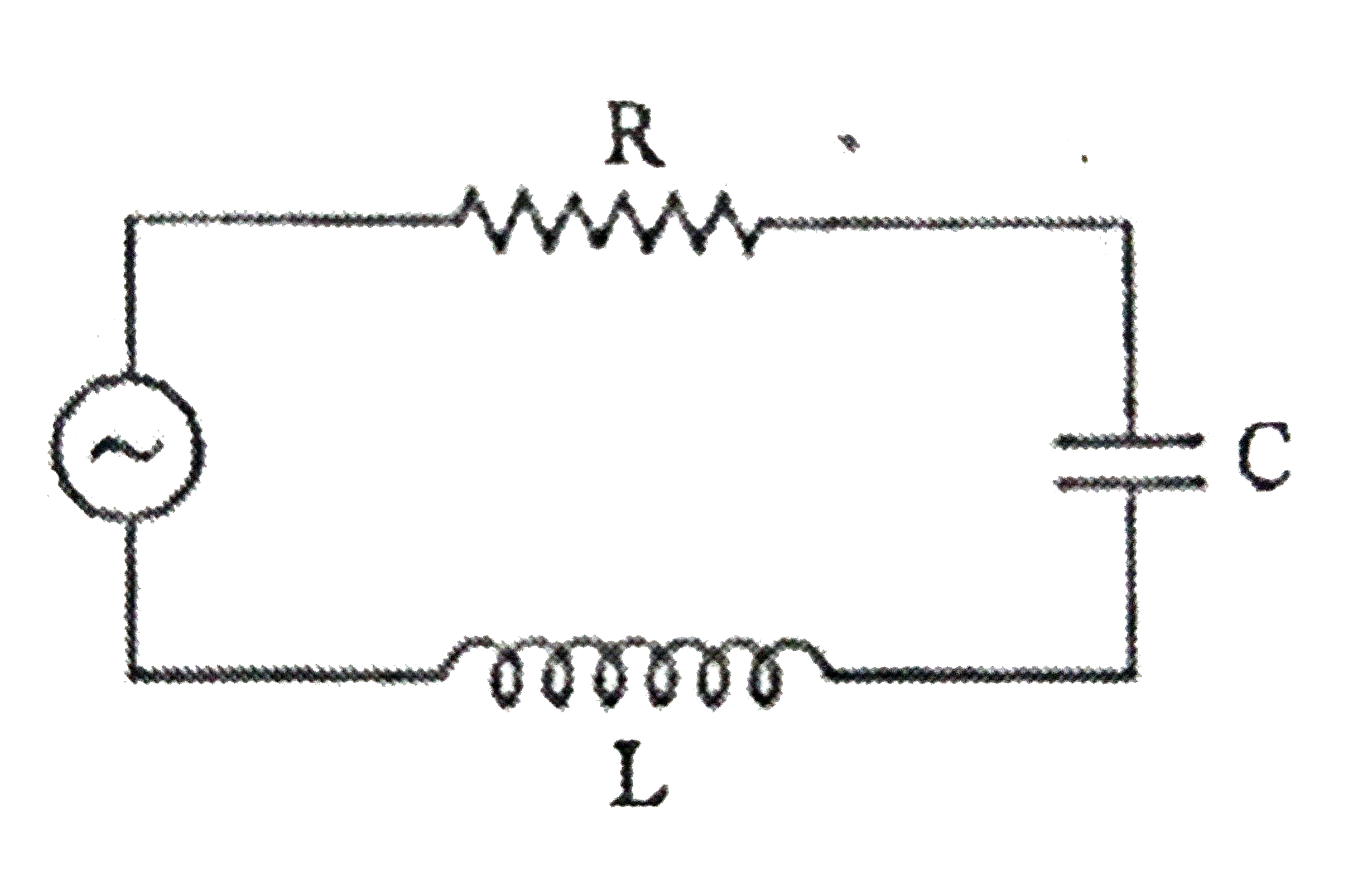
View SolutionThe figure shows a series LCR circuit with L=10.0H2,C=40μF,R=60Ω connected to a variable frequency 240 V source. Calculate
(i) The angular frequency of the source which drives the circuit at resonance.
(ii) The current at the resonating frequency.
(iii) The rms potential drop across the capacitor at resonance.
 View Solution
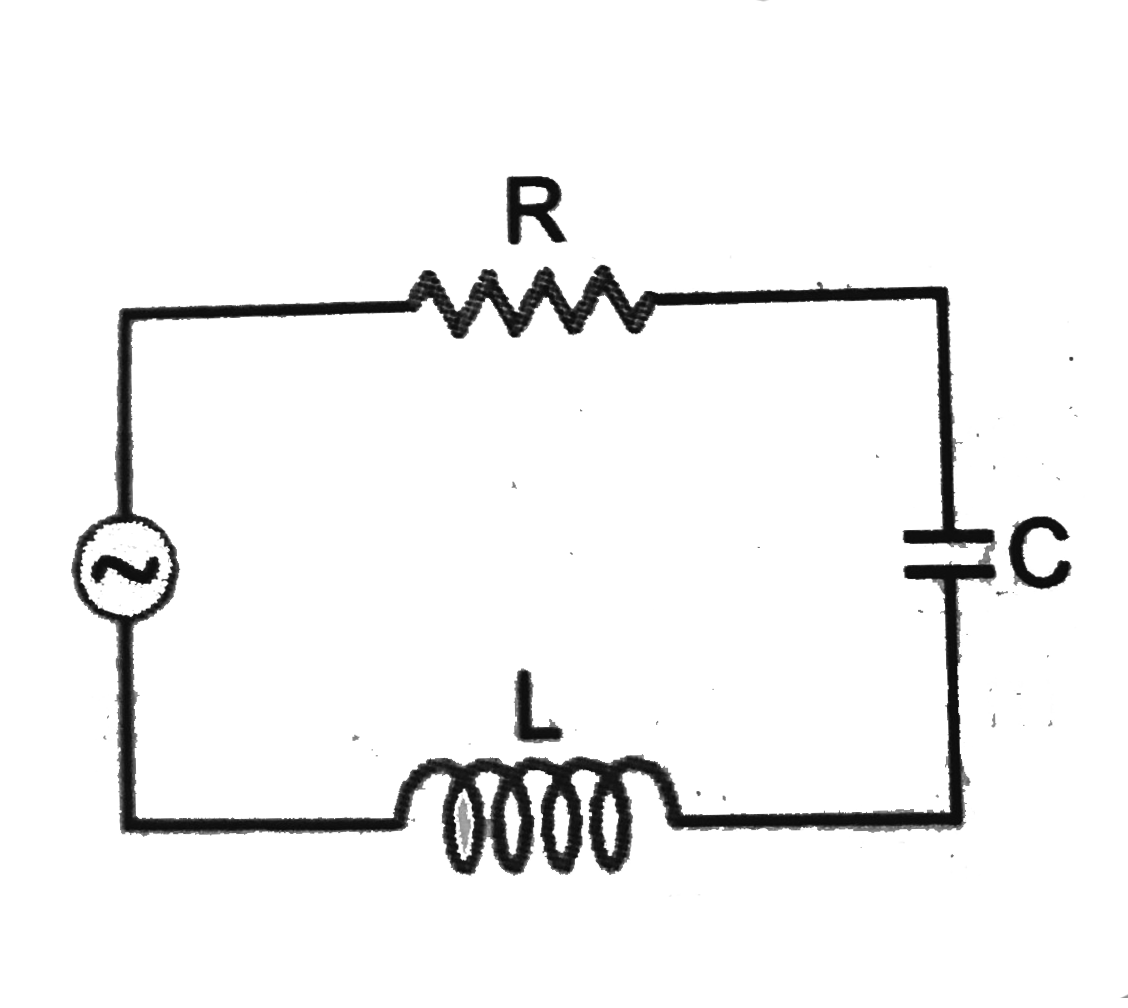
View SolutionFig. shows series LCR circuit with L=5.0H,C=80μF,R=40Ω connected to a variable frequency 240 V source. Calculate
(i) the angular frequency of the source which drives the circuit at resonance.
(ii) Current at the resonating frequency.
(iii) the rms pot. drop across the capacitor at resonance.
 View Solution
View SolutionAn AC voltage source is applied across an R-C circuit. Angular frequency of the source is ω, resistance is R and capacitance is C. The current registered is I. If now the frequency of source is changed to ω2 (but maintaining the same voltage), the current in the circuit is found to be two third. calculate the ratio of reactance to resistance at the original frequency ω .
View SolutionA series LCR circuit with L=4.0H,C=100μF and R=60Ω is connected to a variable frequency 240 V source. Calculate
(i) angular frequency of the source which drives the circuit in resonance,
(ii) current at the resonating frequency,
(iii) rms potential drop across the inductance at resonance.View Solution

