The acceleration of a particle varies with time as shown in .
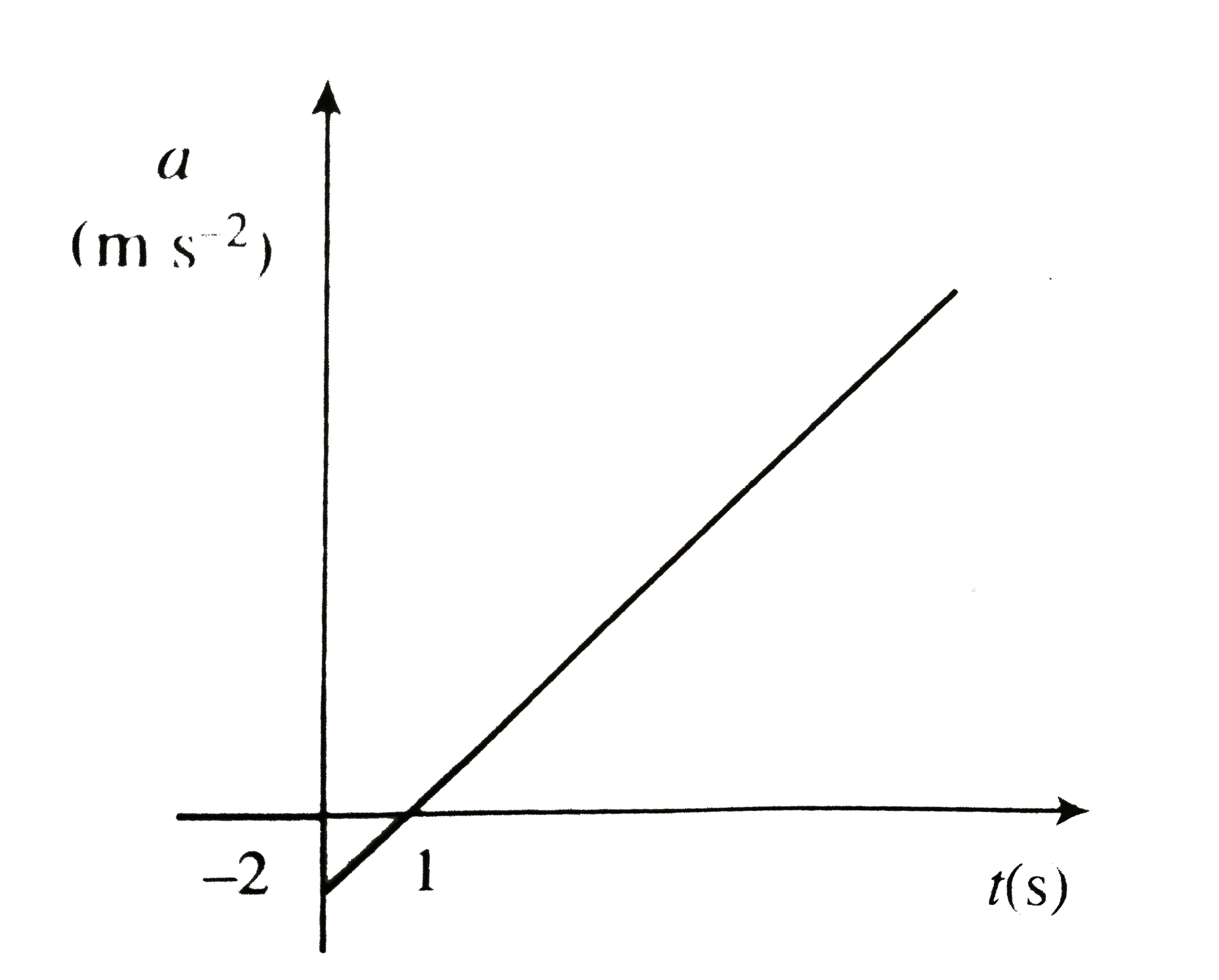 .
.
a. Find an expression for velocityinterms of t. Assume that v=0 at t=0
b. Calculate the displacement of the paarticle in the time interval from t=2s s.
The correct Answer is:a=2t−2
a=t2−2t;
203m
a=2t−2
a. ∫v0dv=∫t0adt⇒v=(2t2/2t)t0=t2−2t
b. S=∫42vdt=(t33−2t22)42=203m.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Single Correct52videos
KINEMATICS-1
- BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Graphical Concept17videos
KINEMATICS-1
- BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Exercise 4.416videos
KINEMATICS-1
- BOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE1videos
GRAVITATION
- BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise Integer9videos
KINEMATICS-2
Similar Questions
The acceleration of particle varies with time as shown.
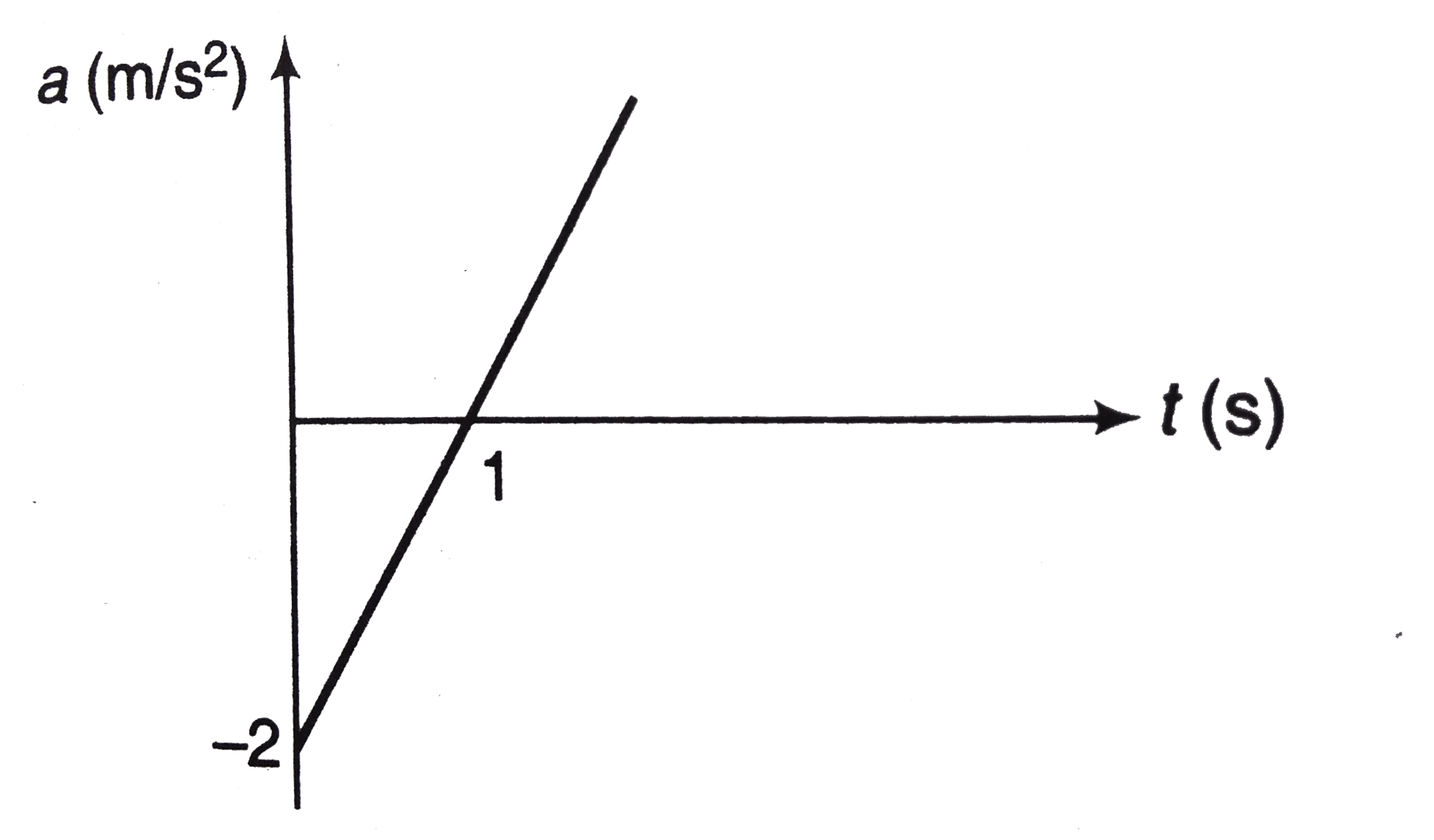
(a) Find an expression for velocity in terms of t.
(b) Calculate the displacement of the particle in the interval from t=2s to t=4s. Assume that v=0 at t=0.View SolutionThe displacement x of a particle varies with time as x=4t2–15t+25. Find the position, velocity and acceleration of the particle at t = 0.
View Solution
Knowledge Check
- Question 1 - Select One
If displacements of a particle varies with time t as s=1t2 , then.
AThe particle is moving with constant velocityBThe particle is moving with variable acceleration of decreasing orderCThe particle is moving with constant retardationDThe particle has constant speed but variable velocity - Question 2 - Select One
A particle is moving with a velocity of v=(3+6t+9t2)ms. Find out
(a) the acceleration of the particle at t=3s.
(b) the displacement of the particle in the interval t=5s to t=8s.A60B20C10D15 - Question 3 - Select One
Velocity of a particle of mass 2kg varies with time t according to the equation →v=(2tˆi+4ˆj)m/s. Here t is in seconds. Find the impulse imparted to the particle in the time interval from t=0 to t=2s.
A2ˆim/sB4ˆim/sC8ˆim/sD6ˆim/s
Velocity of a particle varies with time as v=4t. Calculate the displacement of particle between t=2 to t=4 sec.
View SolutionThe acceleration of a particle varies with time t as
a=t2+t+2
where t is in seconds.
The particle starts with an initial velocity v-3m/s at t=0. find the velocity of the particle at the end of 5s.View SolutionA particle is moving in a straight line and its velocity varies with its displacement as v=√4+4s m/s. Assume s=0 at t=0. find the displacement of the particle in metres at t=1s.
View SolutionFrom the following v-t graph, find the displacement for time interval t=3 to t=12s.
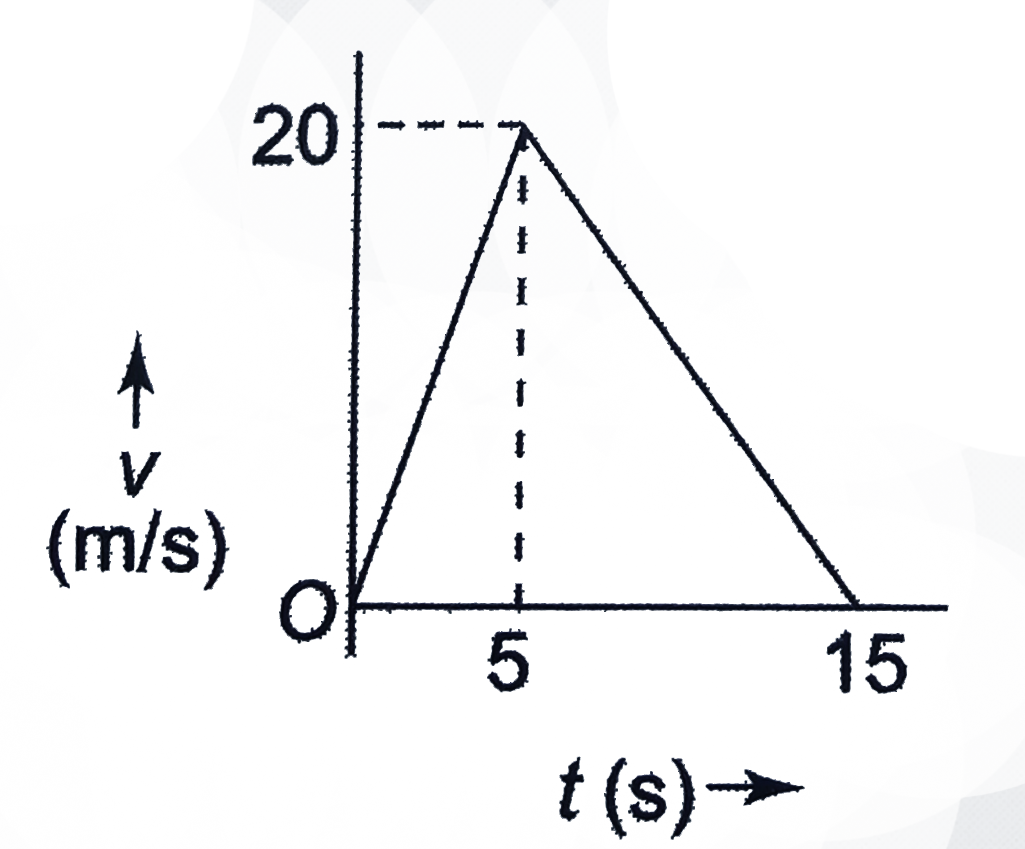 View Solution
View SolutionA starts from rest, with uniform acceleration a. The acceleration of the body as function of time t is given by the equation a = pt, where p is a constant, then the displacement of the particle in the time interval t = 0 to t=t1 will be
View Solution

