The blocks are in equilibrium with a constant horizontal force 2mg acting on block B. The strings are light, find tensions in the strings and values of angles α and β
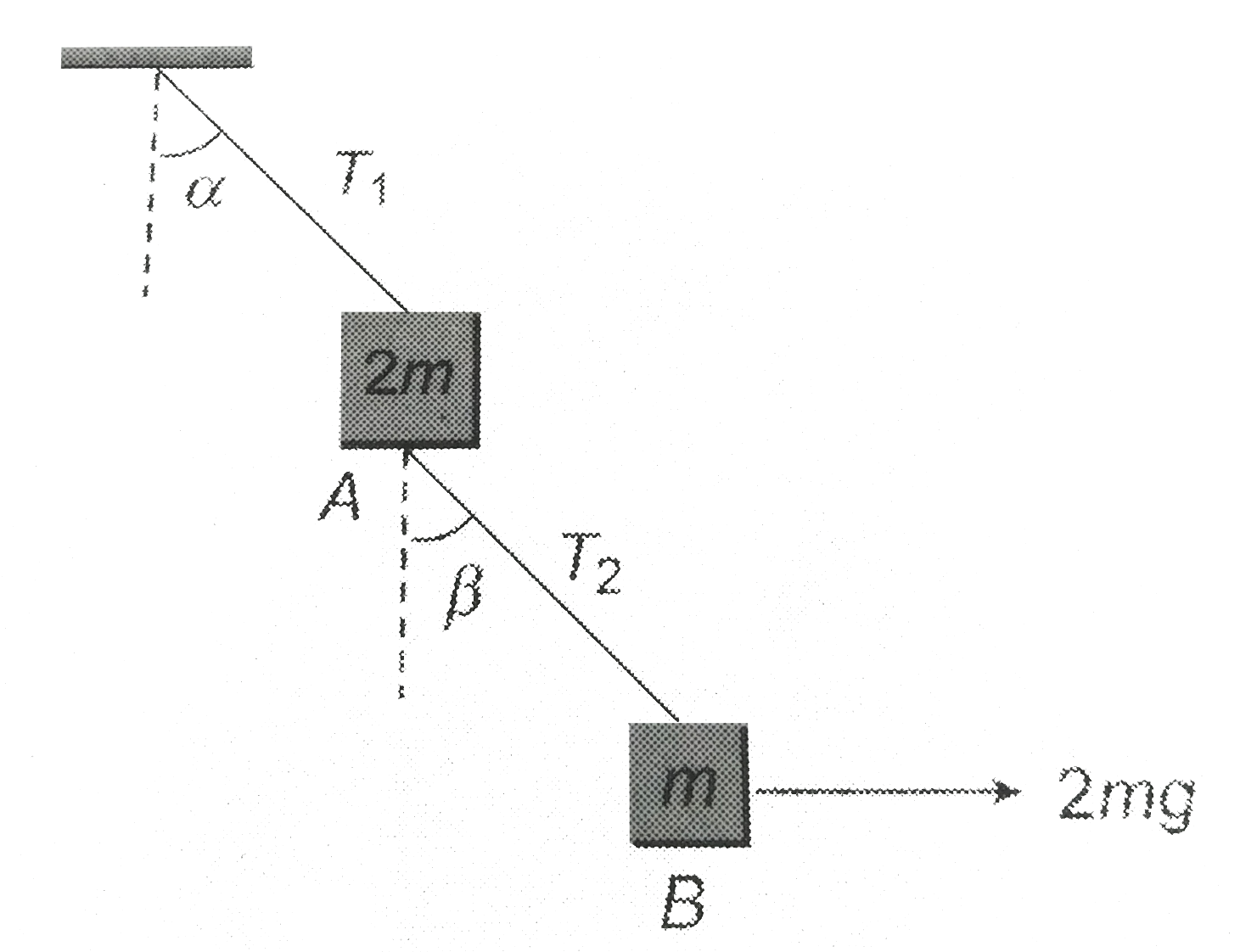
Block B:
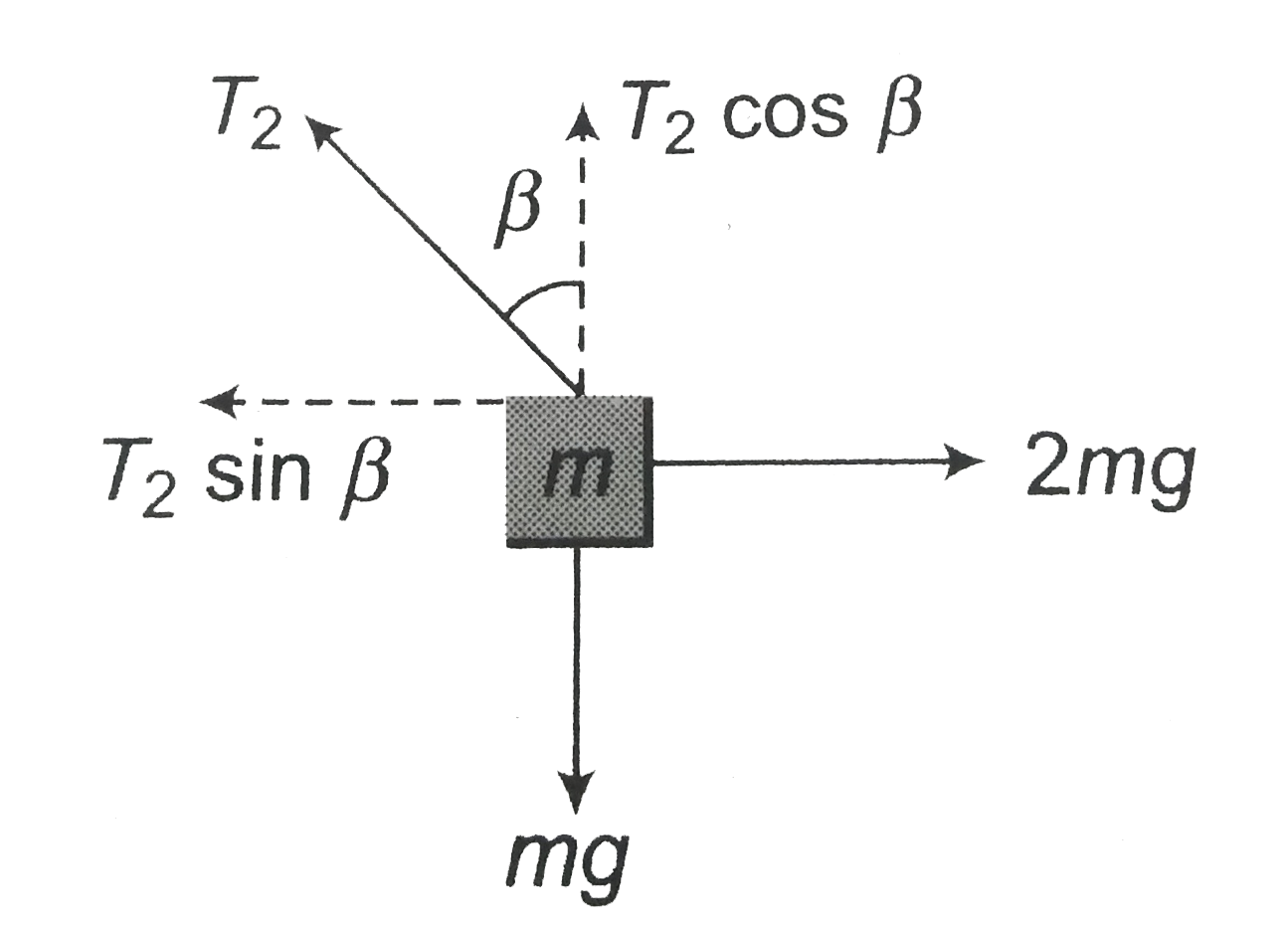
rarr:T_(2)sinbeta=2mg(i)<br>↑⏐:T2cosβ=mg (ii)
T2=√(2mg)2+(mg)2=√5mg
tanβ=2mgmg=2⇒β=tan−1(2)
Block A:

→:T1sinα=T2sinβ=2mg
↑:T1cosα=2mg+T2cosβ
=2mg+mg=3mg
T1=√(2mg)2+(3mg)2=√13mg
tanα=2mg3mg=23⇒α=tan−1(23)
Topper's Solved these Questions
Similar Questions
Knowledge Check
The block of mass m is at rest. Find the tension in the string A .
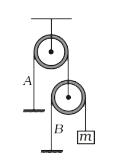 AmgB2 mgC3 mgD4 mg
AmgB2 mgC3 mgD4 mgIn previous question, if a horizontal force F=μmg/2 act on the block and the block remains stationary, then tension in string is.
 AzeroB3μmg2Cμmg2Dnone of thses
AzeroB3μmg2Cμmg2Dnone of thses
Two blocks of masses m and M are connected by an inextensible light string . When a constant horizontal force acts on the block of mass M. The tension in the string is
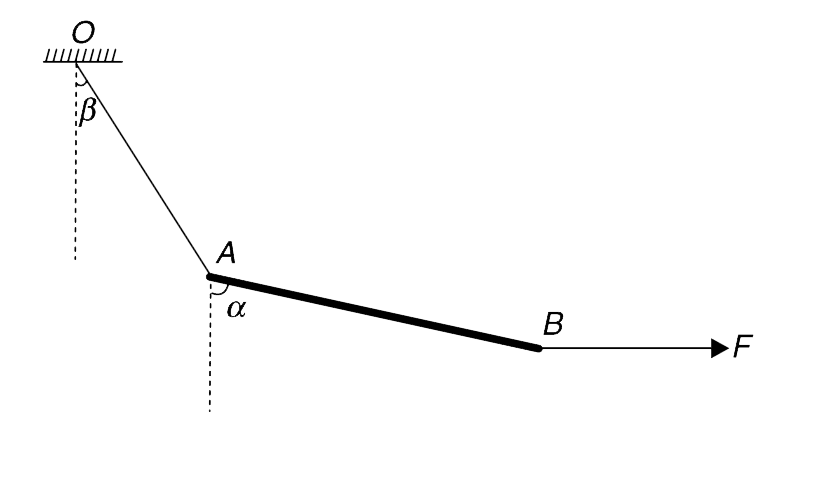
View SolutionA stick AB of mass M is tied at one end to a light string OA. A horizontal force F=Mg is applied at end B of the stick and its remains in equilibrium in position shown. Calculate angles α and β.
View SolutionIn the system shown in figure, the block A is released from rest. Find
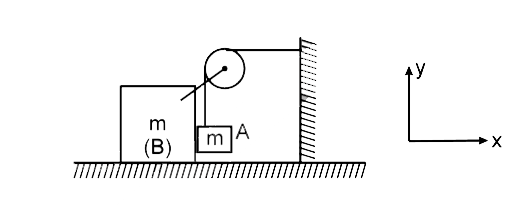
Tension in the string.
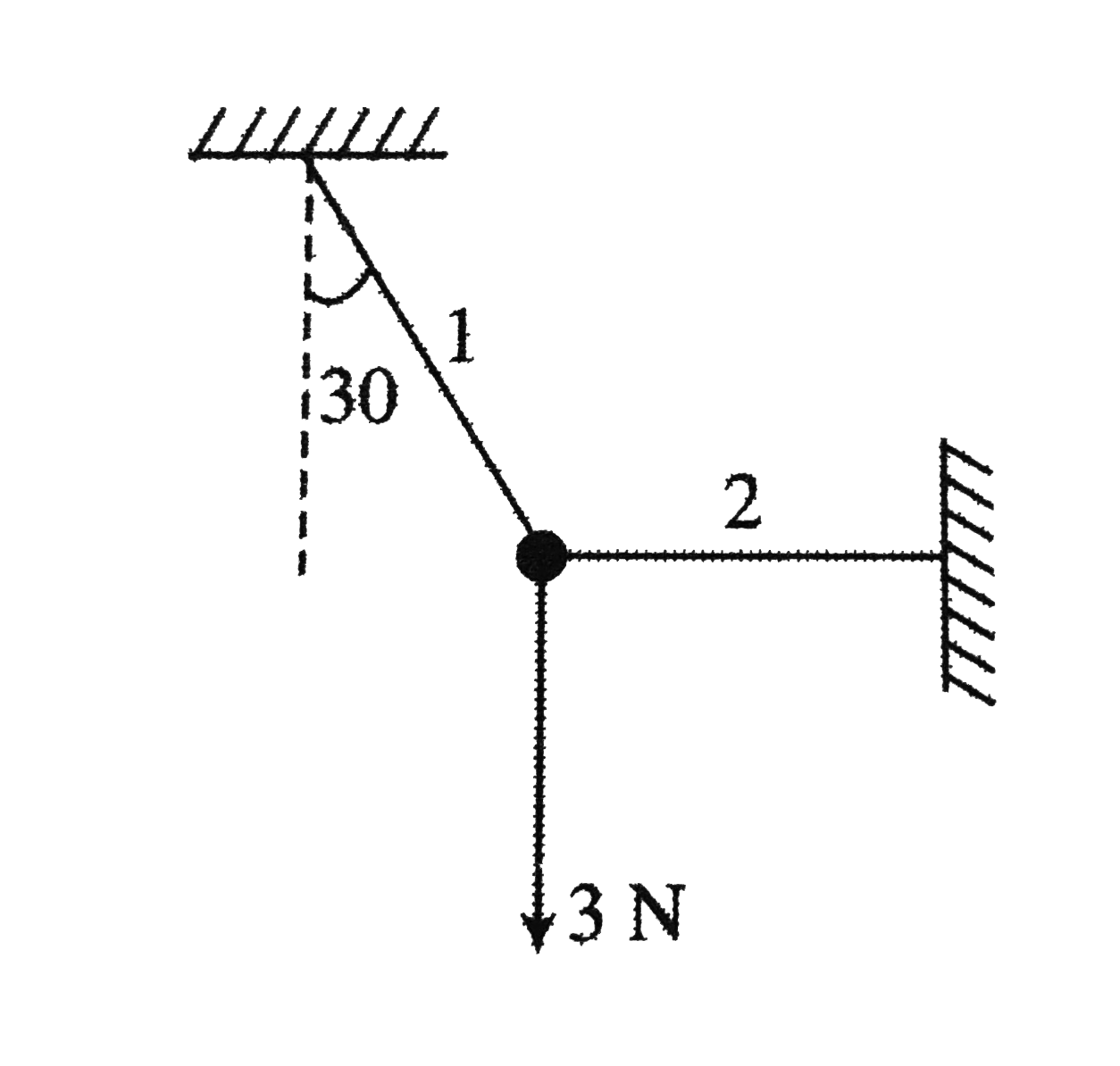
View SolutionA bob of weight 3N is in equilibrium under the action of two string 1 and 2 (figure) . Find the tension forces in the string.
View SolutionThree blocks A, B and C of masses 5 kg, 10 kg and 15 kg respectively connected by two ideal strings are present on a smooth horizontal surface. An external horizontal force of 30 N acts on the block A to pull the system. Find the difference in the tensions in strings connecting A and B and, B and C.
View SolutionThe block A is moving downward with constant velocity v0. Find the velocity of the block B. When the string makes an angle θ with the horizontal
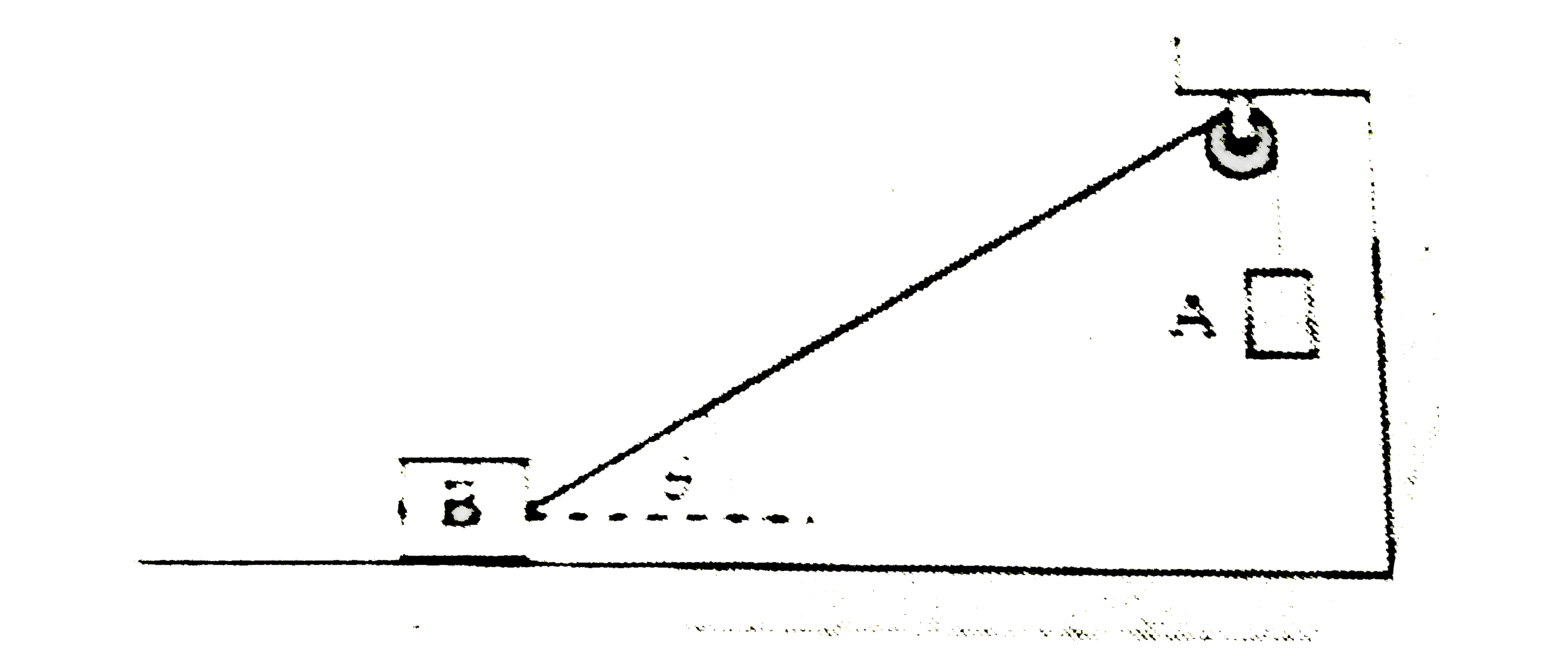
View Solution


