The distance between the two atoms in a diatomic molecule O2 is 1.21×10−10 m. The mass of each oxygen atom is 2.66×10−26 kg. Treating the atoms as point masses find the m moment of inertia of the molecule about an axis passing perpendicular to the line joining the centres of the atoms.
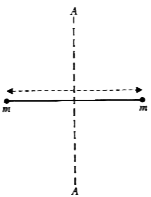
Let the distance between the two atoms be r.
Mass of each atom, m=2.66×10−26 kg
r=1.21×10−10m
M.I. of the two atoms about the axis AB
=m(r2)2+m(r2)2=2×mr24=12mr2
=2.66×10−26×(1.21×10−10)22
=1.95×10−46kgm2
Topper's Solved these Questions
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 1 (CONCEPTUAL SHORT ANSWERS QUESTIONS WITH ANSWERS )
11 Videos
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 1 (LONG ANSWER QUESTIONS)
8 Videos
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - OBJECTIVE QUESTIONS FROM PREVIOUS IAS EXAMINATIONS
50 Videos
Similar Questions
A light rod of length l has two masses m1 and m2 attached to its two ends. The moment of inertia of the system about an axis perpendicular to the rod and passing through the centre of mass is.
View SolutionA diatomic molecule is formed by two atoms which may be treated as mass points m1 and m2 joined by a massless rod of length r. Then the moment of inertia of molecule about an axis passing through centre of mass and perpendicular to the rod is:
View SolutionTwo partcles of masses 1 kg and 2 kg are placed at a distance of 3 m. Moment of inertia of the particles about an axis passing through their centre of mass and perpendicular to the line joining them is (in kg−m2) a) 6 b) 9 c) 8 d) 12
View SolutionTwo masses m1andm2 are placed at a distance r from each other. Find out the moment of inertia of system about an axis passing through their centre of mass.
View SolutionTwo point masses m and 4m are connected by a light rigid rod of length l at the opposite ends. Moment of inertia of the system about an axis perpendicular to the length and passing through the centre of mass is
View SolutionTwo point masses m and 3m are placed at distance r. The moment of inertia of the system about an axis passing through the centre of mass of system and perpendicular to the joining the point masses is
View SolutionMass of an atom of an element X is 2.66×10−23 g. How can this mass be expressed in terms of amu ?
View SolutionThe average mass of an atom of uranium is 3.9×10−25 kg. Find the number of atom is 1 g of uranium.
View SolutionTwo particles of masses m and 2m are placed at separation L. Find the M.I. about an axis passing through the center of mass and perpendicular to the line joining the point masses.
View SolutionTwo spheres each of mass M and radius R/2 are connected with a massless rod of length R. Find the moment of inertia of the system about an axis passing through the centre of one of the sphere and perpendicular to the rod
View Solution
