The electric charges are distributed in a small volume. The flux of the electric field through a spherica surface of radius 10 cm surrounding the total charge is 20V−m. The flux over a concentric sphere of radius 20 cm will be
20 Vm
10 Vm
40 Vm
5 Vm
The correct Answer is:A
To solve the problem, we will use Gauss's Law, which states that the electric flux (Φ) through a closed surface is directly proportional to the charge (Q) enclosed by that surface. The formula for Gauss's Law is given by:
Φ=Qenclosedε0
where:
- Φ is the electric flux through the surface,
- Qenclosed is the total charge enclosed within the surface,
- ε0 is the permittivity of free space.
1. Identify the Given Information:
- The electric flux through a spherical surface of radius 10 cm (Φ₁) is given as 20V⋅m.
- We need to find the electric flux through a concentric spherical surface of radius 20 cm (Φ₂).
2. Apply Gauss's Law to the Inner Sphere:
- According to Gauss's Law, for the inner sphere (radius = 10 cm):
Φ1=Qenclosedε0
- Given that Φ1=20V⋅m, we can express the enclosed charge Qenclosed as:
Qenclosed=Φ1⋅ε0
3. Apply Gauss's Law to the Outer Sphere:
- For the outer sphere (radius = 20 cm), the charge enclosed remains the same since it is concentric and encloses the same volume:
Φ2=Qenclosedε0
- Since Qenclosed is the same for both spheres, we can substitute:
Φ2=Φ1
4. Conclusion:
- Therefore, the flux through the outer sphere (Φ₂) is also:
Φ2=20V⋅m
Final Answer:
The flux over a concentric sphere of radius 20 cm will be 20V⋅m.
---
- Φ is the electric flux through the surface,
- Qenclosed is the total charge enclosed within the surface,
- ε0 is the permittivity of free space.
- The electric flux through a spherical surface of radius 10 cm (Φ₁) is given as 20V⋅m.
- We need to find the electric flux through a concentric spherical surface of radius 20 cm (Φ₂).
- According to Gauss's Law, for the inner sphere (radius = 10 cm):
Φ1=Qenclosedε0
- Given that Φ1=20V⋅m, we can express the enclosed charge Qenclosed as:
Qenclosed=Φ1⋅ε0
- For the outer sphere (radius = 20 cm), the charge enclosed remains the same since it is concentric and encloses the same volume:
Φ2=Qenclosedε0
- Since Qenclosed is the same for both spheres, we can substitute:
Φ2=Φ1
- Therefore, the flux through the outer sphere (Φ₂) is also:
Φ2=20V⋅m
The flux over a concentric sphere of radius 20 cm will be 20V⋅m.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Assertion and Reason
15 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Match the columns
5 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Check point 1.5
20 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions
135 Videos
Similar Questions
Electric charge are distributed in a small volume. The flux of the electric field through a spherical surface of radius 10cm surrounding the total charge is 25 V m. The flux over a concentric sphere of radius 20 cm will be
View SolutionThe flux of electric field through the circular region of radius r as shown in the figure is
_PHY_E05_291_Q01.png)
View SolutionFind the flux due to the electric field through the curved surface (R is radius of curvature)

View SolutionA charge Q is placed at the centre of a cube. Find the flux of the electric field through the six surfaced of the cube.
View SolutionFigure shown below is a distribution of charges. The flux of electric field due to these charges through the surface S is
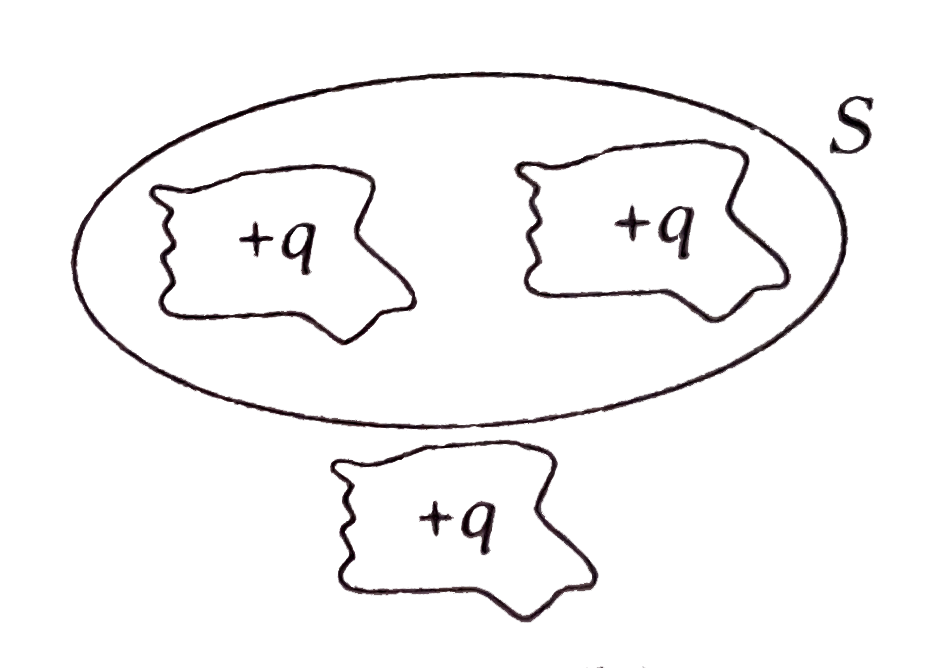
View SolutionFigure shown below is a distribution of charges. The flux of electric field due to these charges through the surface S is

View SolutionA capacitor of capacitance C is charged to a potential V. The flux of the electric field through a closed surface enclosing the capacitor is
View SolutionA charge q is placed at the centre of the open end of a cylindrical vessel . The flux of the electric field through the surface of the vessel is

View SolutionThe magnitude of the electric field on the surface of a sphere of radius r having a uniform surface charge density σ is
View SolutionFind the flux of the electric field through each of the five surfaces of the inclined plane as shown in figure. What is the total flux through the entire closed surface?

View Solution
