The flexible bicycle type chain of length πr2 and mass per unit length ρ is released from rest with θ=0∘ In the smooth circular channel and falls through the hole in the supporting surface, Determine the velocity v of the chain as the last link leaves the slot.
 .
.
The correct Answer is:B, D
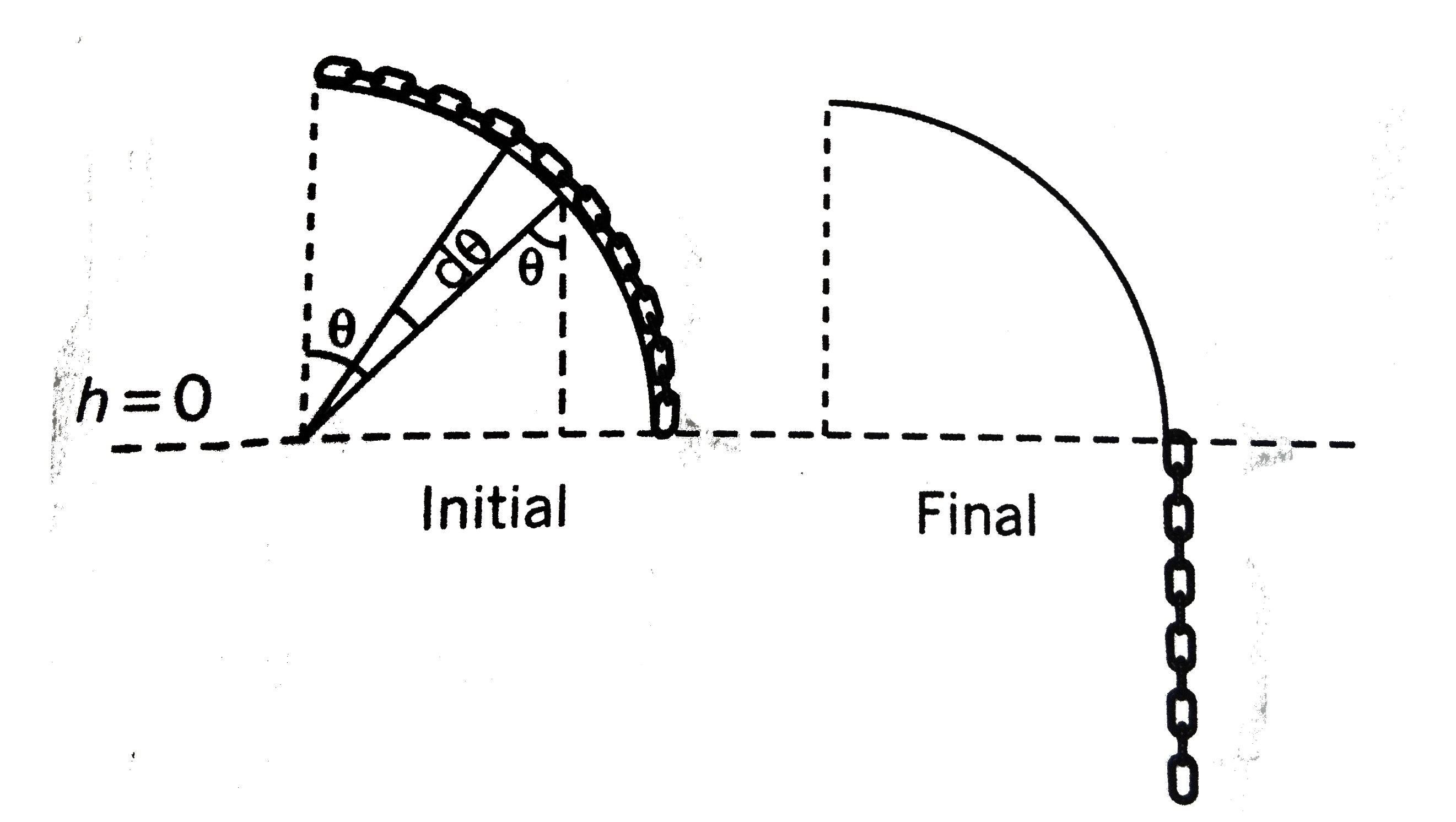
Initial PE,
Ui=∫θ=π/2θ=0∘(rdθ)(ρ)(g)(rcosθ)
=(ρgr2)[sinθ]π/20=ρgr2
Find PE,
Uf=(πr2×ρ)(g)(−πr/22)=−π2r2ρg8
ΔU=r2ρg(1+π18)
DehtaU=KE
ΔU=KE
or r2gh(1+π28)=12(πr2)(ρ)v2
⇒v=√4rg(1π+π8)
or v=√rg(π2+4π).
Topper's Solved these Questions
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based
2 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 More Than One Correct
9 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question
11 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY
33 Videos
Similar Questions
A heavy chain with a mass per unite length p is pulled by the constant force F along a horizental surface consisting of a smooth section and a rough section. The chain is initially at rest on the rough surface with x=0 . If the coefficient of kinetic friction between the chain and the rough surface is μk determine the velocity v of the chain when x=L . The force F is hreater than μkogL in under to initate the motion ,

View SolutionA chain of mass m and length L is held at rest on smooth horizontal surface such that a part I of the chain is hanging vertically from the table. If the chain is let go, what is its speed as its end just leaves the horizontal surface?
View SolutionA flexible steel cable of total length L and mass per unit length μ hangs vertically from a support at one end. (a) Show that the speed of a transverse wave down the cable is v=√g(L−x), where x is measured from the support. (b) How long will it takes for a wave to travel down the cable?
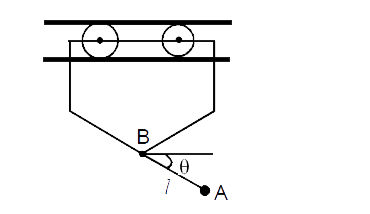
View SolutionThe simple pendulum A of mass mA and length l is suspended from the trolley B of mass mB. If the system is released from rest at θ=0, determine the velocity vB of the trolley when θ=90°. Friction is negligible.
View SolutionA rope of length 5 m has uniform mass per unit length. λ=2kgm The rope is pulled by a constant force of 10N on the smooth horizontal surface as shown in figure The tension in the rope at x = 2 m from polit A is
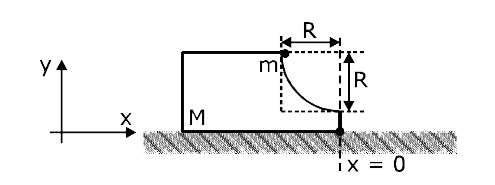
View SolutionA block of mass M has a circular cut with a frictionless surface as shown. The block rests on the horizontal frictionless surface of a fixed table. Initially the right edge of the block is at x = 0, in a co-ordinate system fixed to the table. A point mass m is released from rest at the topmost point of the path as shown and it slides down. When the mass loses contact with the block, its position is x and the velocity is v. At that instant, which of the following options is/are correct?
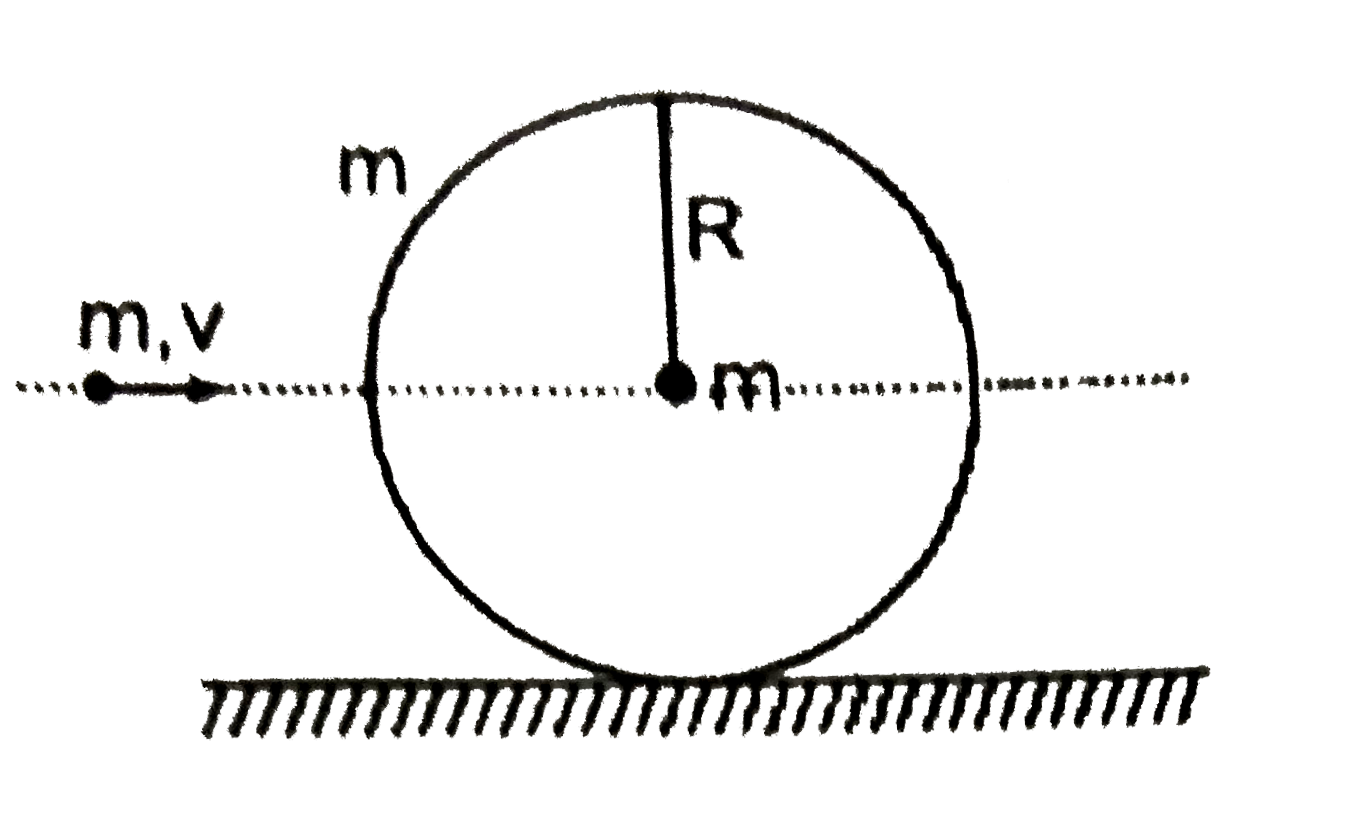
View SolutionA hollow sphere of mass 'm' and radius R rests on a smooth horizontal surface. A simple pendulum having string of length R and bob of mass m hangs from top most point of the sphere as shown. A bullet of mass 'm' and velocity 'v' partially penetrates the left side of the sphere and stick to it. The velocity of the sphere just after collision with bullet is .
View SolutionA very flexible uniform chain of mass M and length L is suspended vertically so that its lower and just touches the surface of a table. When the upper end of the chain is released it falls with each link coming to rest the instant it strikes the table. Find the force exerted by the chain on the table at the moment when y part of the chain has already rested on the table.
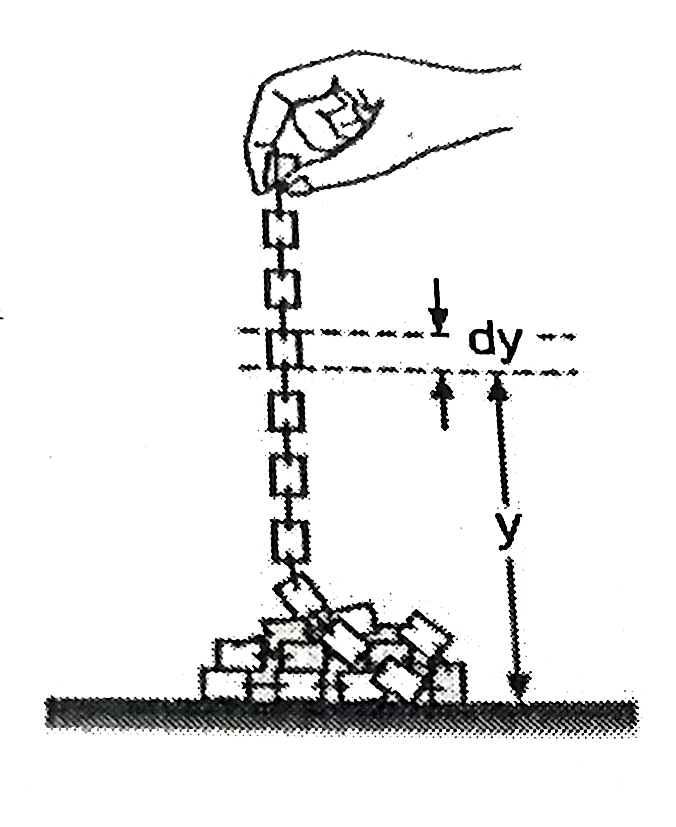
View SolutionA smooth chain (AB) of mass (m) rests against a surface in the form of a quarter of circle of radius R. If it is released from rest, the form of a quarter of a circle of radius R. If it is releaded from, the velocity of the chain after it comes over the horizontal part of the surface is .

View SolutionA conducting circular loop of radius a and resistance per unit length R is moving with a constant velocity v0 , parallel to an infinite conducting wire carrying current i0. A conducting rod of length 2a is approaching the centre of the loop with a constant velocity v02 along the direction 2 of the current. At the instant t=0, the rod comes in contact with the loop at A and starts sliding on the loop with the constant velocity. Neglecting the resistance of the rod and the self-inductance of the circuit, find the following when the rod slides on the loop.
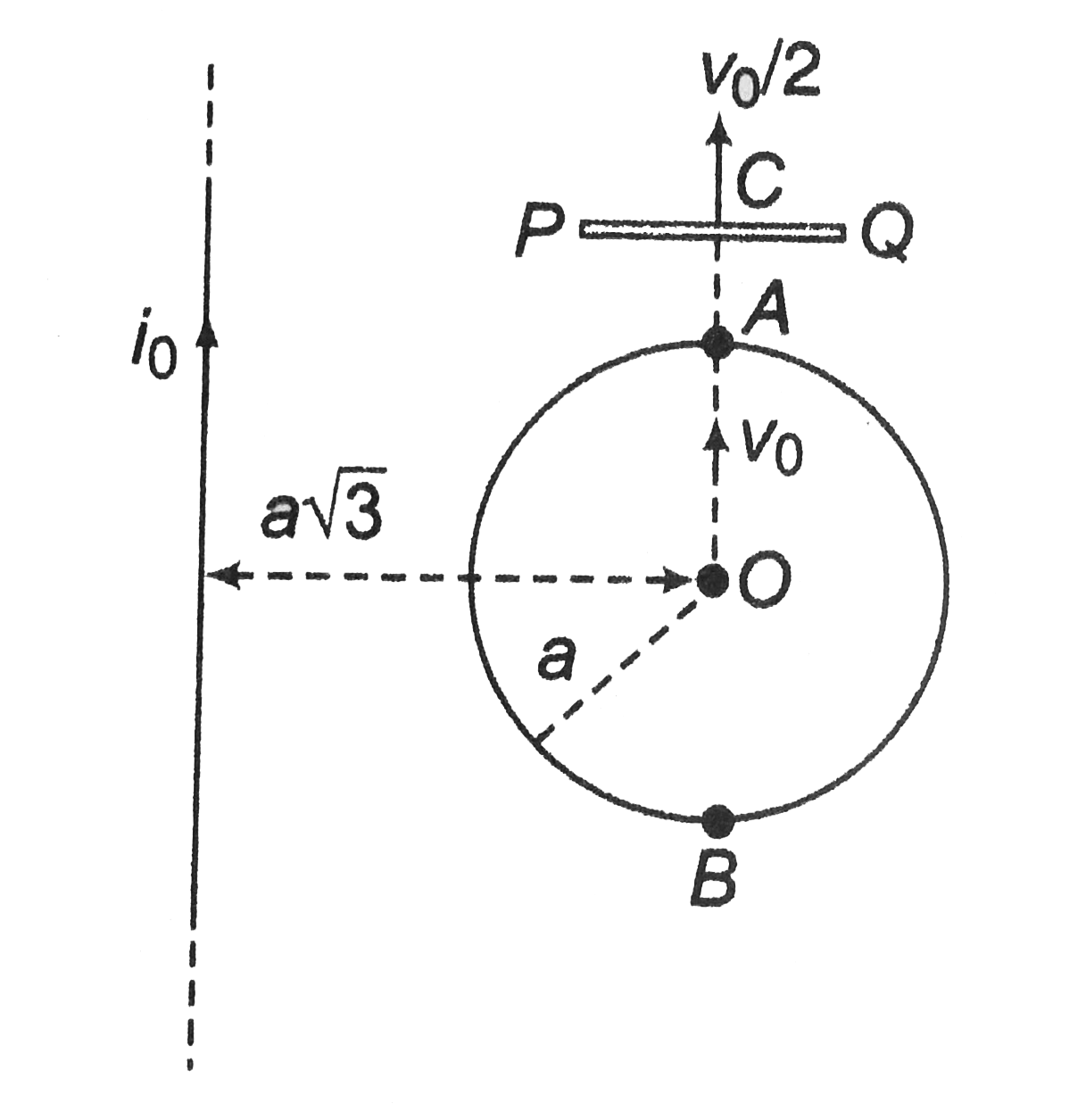
(a) The current through the rod when it is at a distance of (a2) from the point A of the loop.
(b) Force required to maintain the velocity of the rod at that instant.
View Solution