The fringe width in Young’s double slit experiment increases when
Fringe Width. It is the distance between any two successive fringes in interference pattern.
Let S1,S2 be the two fine slits illuminated by a monochromatic sources of wavelength λ.
Intensity of light at any point P on the screen at a distance D from the slit depends upon the path difference between S2P and S1P.
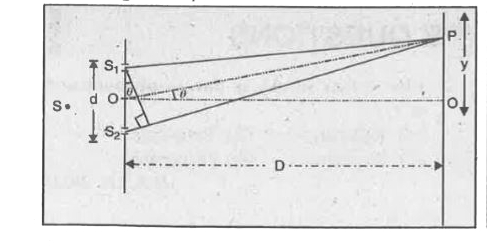
From S1 draw S1A perpendicular to S2P. Since ∠S2S1A→θ [D is very large as compared to d], therefore, ∠S1AS2→90∘ and AP≈S1P.
∴Path difference=S2P−S1P=(S2A+AP)−S1P or Path difference=S2A=dsinθ
Since θ is very small, sinθ can be replaced by tanθ .
∴Path difference=dtanθ=dyD
Constructive interference [Bright Fringes). For bright fringes, the path difference should be equal to an even multiple of λ/2.
∴dyD=2nλ2=nλ
or y=nλDd
If n = 0, y0=0, which is the position of central maxima.
If n = 1, y1=Ddλ, which is the position of first maxima.
If n = 2, y2=2Ddλ, which is the position of
Similarly yn−1=(n−1)Ddλ
and yn=nDdλ
Fringe width β=yn−y(n−1)=Ddλ[n−(n−1)]
β=Ddλ ...(i)
Destructive interference [Dark Fringes]. For dark fringes, the path difference should be an old multiple of 1/2.
dDy=(2n−1)λ2
or y=Dd(2n−1)λ2
If n = 1, y1=Ddλ2, which is the position of 1st minima.
If n = 2, y1=Dd2λ2, which is the position of 2nd minima.
If n = 3, y1=Dd3λ2, which is the position of 3rd minima.
∴ Fringe width, β=y3−y2=Ddλ
or β=Ddλ ...(ii)
From (i) and (ii), we conclude that bright and dark fringes have equal fringe width.
β∝D
∝λ
∝1d
If d = 0, β=∞ i.e. dark and bright bands will be infinitely well spaced and there will be uniform illumination.
Topper's Solved these Questions
- OPTICSBOOK - MBD -HARYANA BOARDCHAPTER - OPTICSEXERCISE - OBJECTIVE TYPE QUESTIONS
26 Videos
- OPTICSBOOK - MBD -HARYANA BOARDCHAPTER - OPTICSEXERCISE - SHORT ANSWER TYPE QUESTIONS
46 Videos
- MODEL TEST PAPER - 2BOOK - MBD -HARYANA BOARDCHAPTER - MODEL TEST PAPER - 2EXERCISE - SET - D ( LONG ANSWER TYPE QUESTIONS)
4 Videos
- PRINCIPLES OF COMMUNICATIONBOOK - MBD -HARYANA BOARDCHAPTER - PRINCIPLES OF COMMUNICATIONEXERCISE - Objective Type Questions
19 Videos
Similar Questions
How does the fringe width, in Young's double-slit experiment, change when the distance of separation between the slits and screen is doubled ?
View SolutionWith a monochromatic light, the fringe-width obtained in a Young’s double slit experiment is 0.133 cm. The whole set- up is immersed in water of refractive index 1.33, then the new fringe-width is
View Solution
Knowledge Check
The fringe width in Young's double slit experiment can be increased by decreasing
Aseparationk between two slits.Bwidth of the slit.Cwavelength of lightDdistance between slit and the screen.The fringe width in a Young's double slit experiment can be increased. If we decrease
AWidth of the slitsBSeparation of the slitsCWavelength of the light usedDDistance between slits and screenThe fringe width in a Young's double slite experiment can be increased by decreasing
Aseparation of the slitsBfrequency of the source of lightCdistance between the slit and the screenDwavelength of the source of light
Find the angular fringe width in Young's double slit experiment using a monochromatic light of wavelength 500 nm when the slits are separated by 2.5 mm.
View SolutionFind out the expression for Fringe width in Young's double' slit' 'experiment.
View SolutionHow would the angular separation of interference fringes in Young's double slit experiment change when the distance of separation between slits and screen is doubled ?
View SolutionHow would the angular separation of interference fringes in Young's double-slit experiment change when the distance between the slits and screen is doubled ?
View SolutionThe shape of the interference fringes in Young’s double slit experiment when D (distance between slit and screen) is very large as compared to fringe width is nearly
View Solution
