The insulated spheres of radii R1 and R2 having charges Q1 and Q2 respectively are connected to each other. There is
an increase in the energy of the system
no change in the energy of the system
always decrease in energy
a decrease in energy of the system unless Q1R2=Q2R1
The correct Answer is:D
To solve the problem, we need to analyze the situation where two insulated spheres with radii R1 and R2 and charges Q1 and Q2 are connected. The charges will redistribute until both spheres reach the same electric potential.
1. Understanding Electric Potential:
The electric potential V due to a charged sphere at its surface is given by the formula:
V=kQR
where k is Coulomb's constant, Q is the charge, and R is the radius of the sphere.
2. Setting Up the Equation:
When the two spheres are connected, they will reach the same potential. Therefore, we can write:
V1=V2
Substituting the formula for electric potential, we have:
kQ1R1=kQ2R2
3. Canceling Out Constants:
Since k is a constant, we can cancel it from both sides:
Q1R1=Q2R2
4. Cross Multiplying:
Rearranging the equation gives:
Q1R2=Q2R1
5. Interpreting the Result:
This equation indicates that the product of the charge on one sphere and the radius of the other sphere must be equal. This condition must hold true for the system to reach equilibrium.
6. Energy Consideration:
When the charges redistribute, the total energy of the system decreases as it moves towards a more stable configuration. Thus, we conclude that there is a decrease in energy of the system unless the condition Q1R2=Q2R1 is satisfied.
Final Answer:
The correct conclusion is that there will be a decrease in energy of the system unless Q1R2=Q2R1.
---
The electric potential V due to a charged sphere at its surface is given by the formula:
V=kQR
where k is Coulomb's constant, Q is the charge, and R is the radius of the sphere.
When the two spheres are connected, they will reach the same potential. Therefore, we can write:
V1=V2
Substituting the formula for electric potential, we have:
kQ1R1=kQ2R2
Since k is a constant, we can cancel it from both sides:
Q1R1=Q2R2
Rearranging the equation gives:
Q1R2=Q2R1
This equation indicates that the product of the charge on one sphere and the radius of the other sphere must be equal. This condition must hold true for the system to reach equilibrium.
When the charges redistribute, the total energy of the system decreases as it moves towards a more stable configuration. Thus, we conclude that there is a decrease in energy of the system unless the condition Q1R2=Q2R1 is satisfied.
The correct conclusion is that there will be a decrease in energy of the system unless Q1R2=Q2R1.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (B) Chapter exercises
17 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.5
20 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
Two non-conduction hollow uniformly charged spheres of radil R1 and R2 with charge Q1 and Q2 respectively are places at a distance r. Find out total energy of the system.

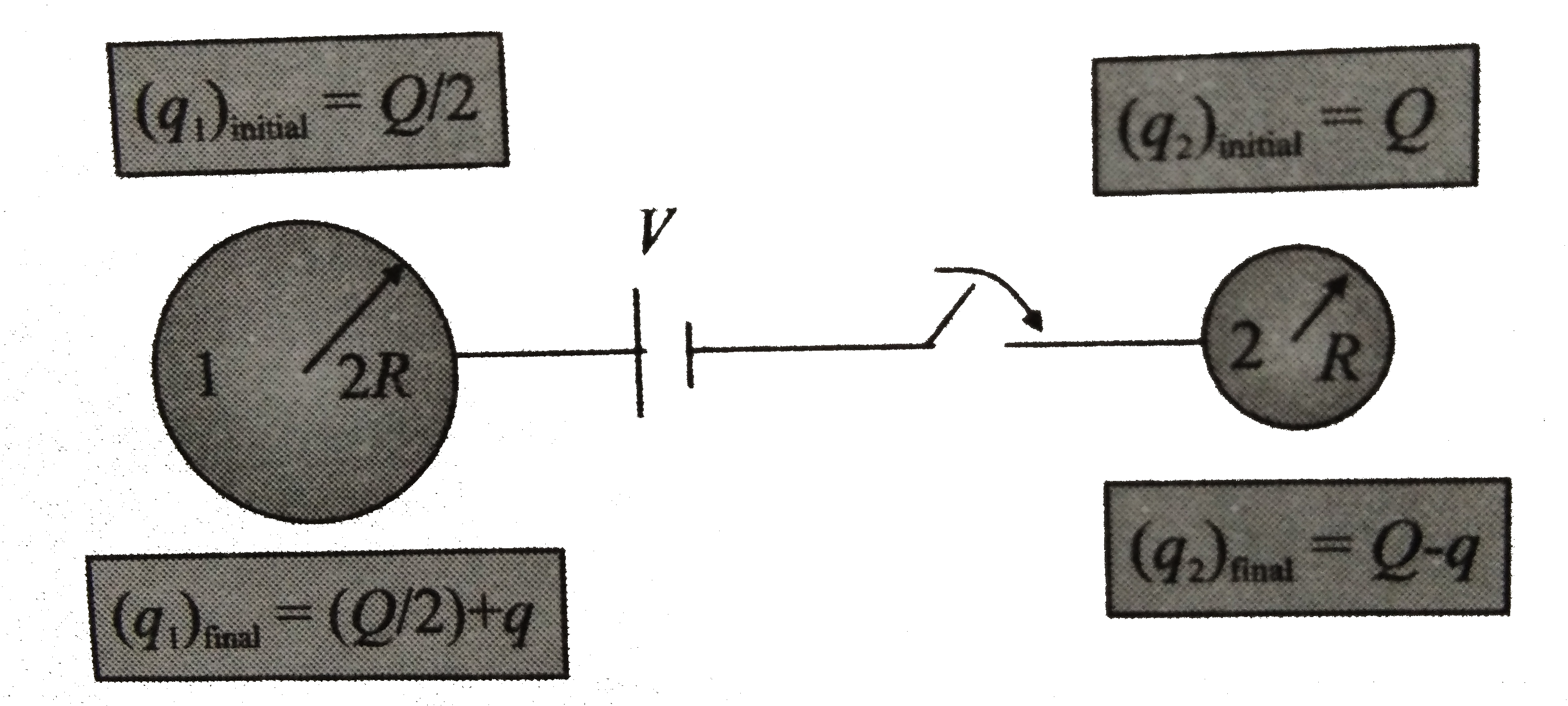
View SolutionThere are two spheres of radii R and 2R having charges Q and Q/2, respectively. These two spheres are connected with a cell of emf V volts as show in. When the switch is closed, find the final charge on each sphere.
View SolutionTwo concentric, thin metallic spheres of radii R1andR2(R1>R2) charges Q1andQ2 respectively Then the potential at radius r between R1andR2 will be (k=1/4π∈)
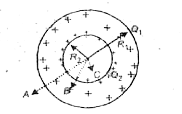
View SolutionYou are given two concentric charged conducting spheres of radii R1andR2 such that R1>R2, having charges Q1andQ2 respectively and uniformly distributed over its surface. Calculate E and V at three points A, B , C whose distances from the centre are rA,rBandrc respectively as shown in figure.
View SolutionTwo concentric conducting shells of radii R and 2R are having charges Q and -2Q respectively.In a region r
View SolutionFind force acting between two shells of radius R1 and R2 which have uniformly distributed charges Q1 and Q2 respectively and distance between their centres is r.

View SolutionTwo concentric uniformly charge spherical shells of radius R1 and R2(R2>R1) have total charges Q1 and Q2 respectively. Derive an expression of electric field as a function of r for following positions.
(i) r<R1 (ii) R1≤r<R2
(iii) r≥R2

View SolutionConcentric metallic hollow spheres of radii R and 4R hold charges Q1andQ2 respectively. Given that surface charge densities of the concentric spheres are equal, the potential difference V(R)−V(4R) is :
View SolutionTwo concentric spherical conducting shells of radii R and 2R are carrying charges q and 2q, respectively. Both are now connected by a conducting wire. Find the change in electric potential (inV) on the outer shell.
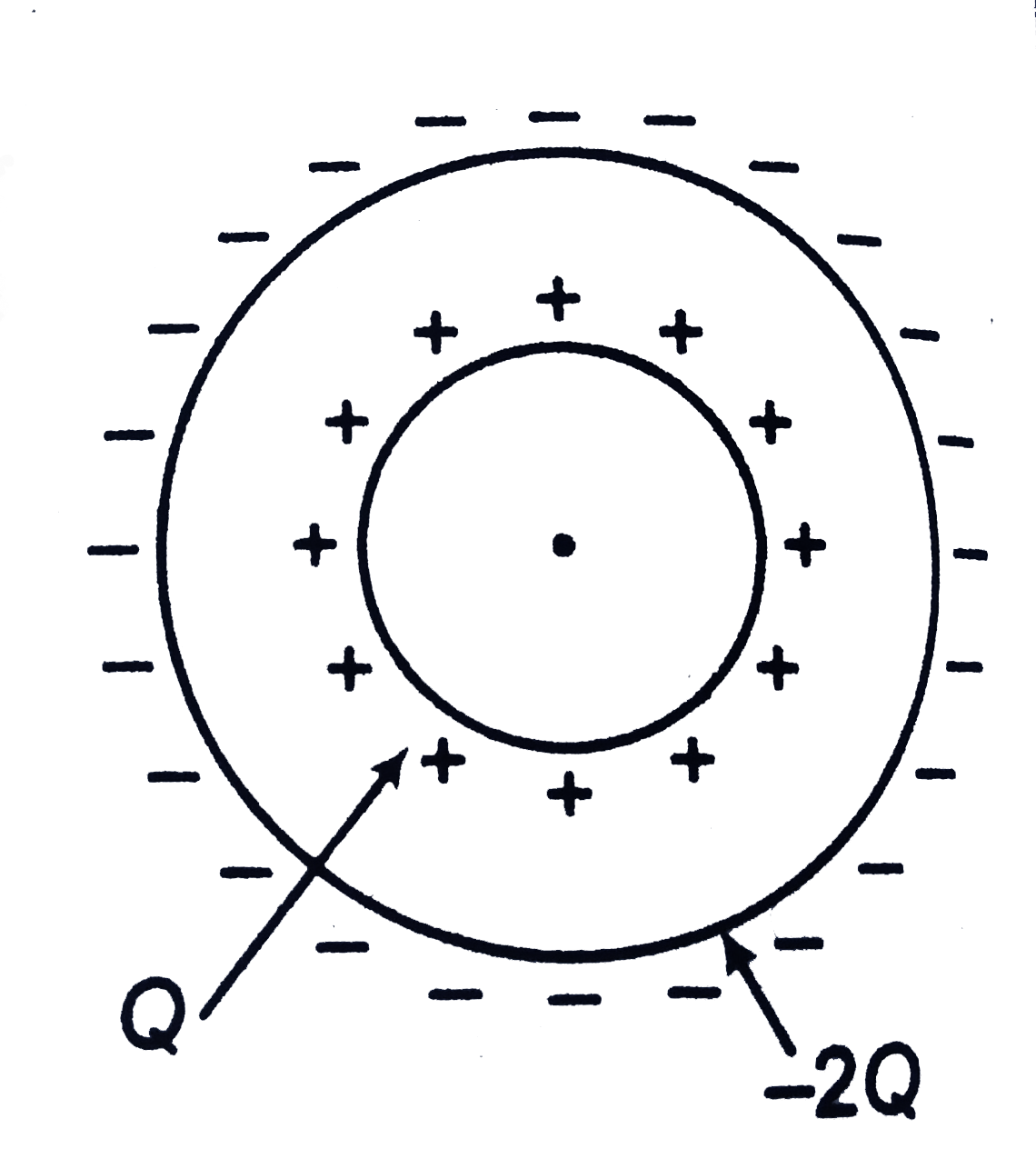
View SolutionTwo concentric conducting spheres of radii R and 2R are crrying charges Q and −2Q, respectively. If the charge on inner sphere is doubled, the potetial differece between the two spheres will
View Solution
