The magnetic field exists along negative x-axis and electric field exists along positive x-axis. A charged particle moves with a velocity inclined at an angle (θ) with vertical in (x-y) plane. What will be the correct diagram of the helical path?
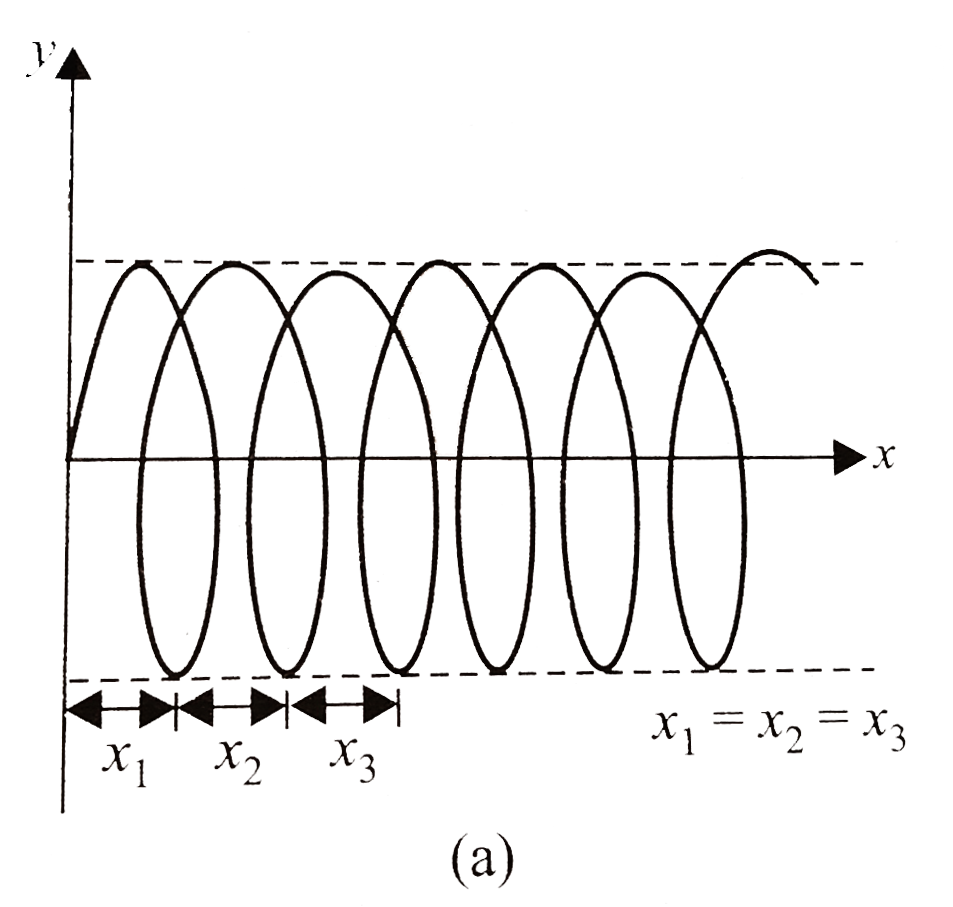
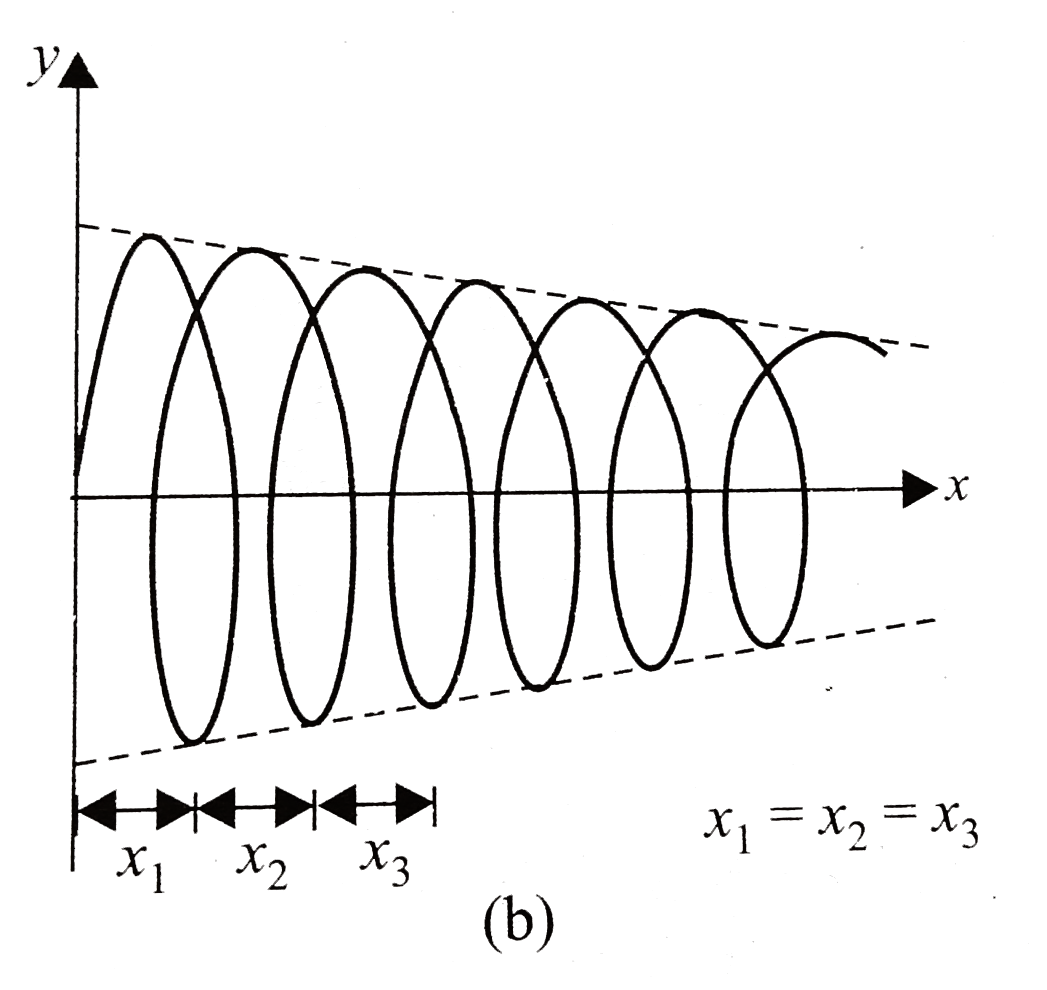
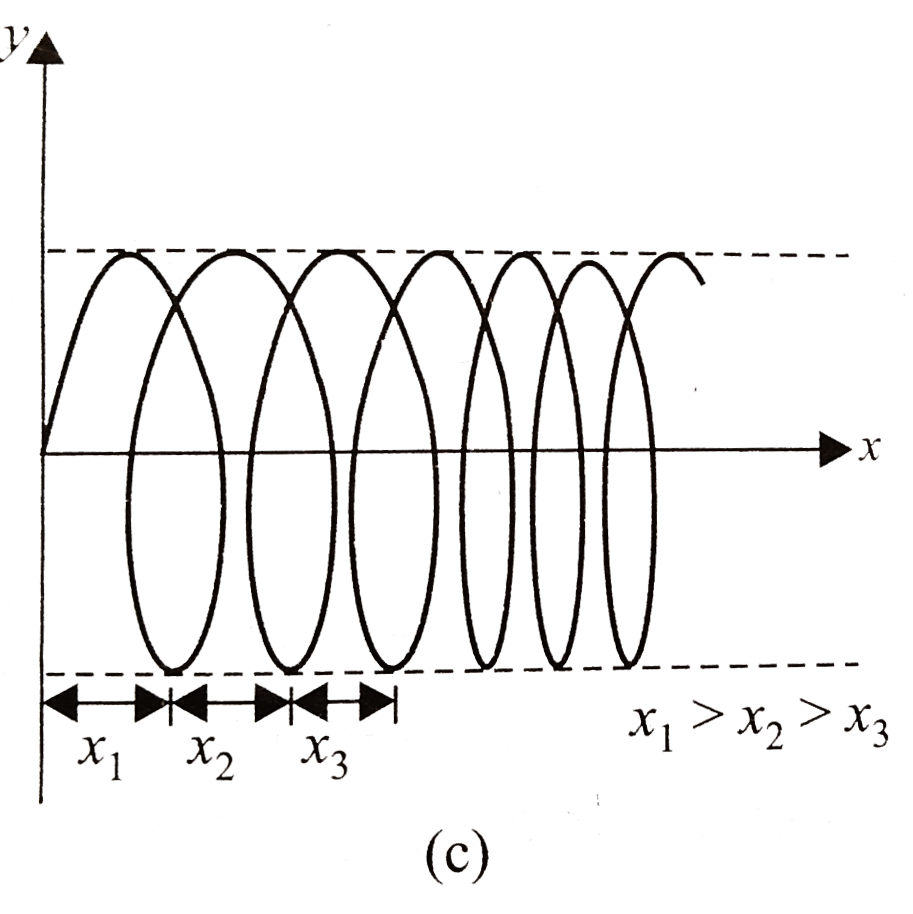

The correct Answer is:D
To solve the problem, we need to analyze the motion of a charged particle in the presence of both electric and magnetic fields. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the Fields
- The magnetic field (B) is directed along the negative x-axis.
- The electric field (E) is directed along the positive x-axis.
Step 2: Analyze the Velocity of the Charged Particle
- The charged particle moves with a velocity (V) that is inclined at an angle (θ) with the vertical in the x-y plane.
- We can resolve this velocity into two components:
- Vertical Component (V_y): This is the component of velocity in the y-direction, given by Vy=Vcos(θ).
- Horizontal Component (V_x): This is the component of velocity in the x-direction, given by Vx=Vsin(θ).
Step 3: Determine the Forces Acting on the Particle
- The particle experiences a magnetic force due to the magnetic field. The magnetic force (F_m) is given by:
Fm=q(Vy×B)
where q is the charge of the particle and B is the magnetic field strength. Since the magnetic field is along the negative x-axis, the force will act in a direction perpendicular to both the velocity and the magnetic field.
- The particle also experiences an electric force (F_e) due to the electric field, which is given by:
Fe=qE
This force acts in the positive x-direction.
Step 4: Motion of the Particle
- The component of velocity perpendicular to the magnetic field (V_y) will cause the particle to move in a circular path due to the magnetic force.
- The electric field will exert a constant force in the positive x-direction, resulting in an acceleration in that direction.
Step 5: Resulting Path of the Particle
- The combination of circular motion due to the magnetic field and linear acceleration due to the electric field results in a helical path.
- As the particle accelerates in the x-direction, the radius of the circular motion remains constant, but the pitch of the helix increases.
Step 6: Identify the Correct Diagram
- The correct diagram should show a helical path that is increasing in the x-direction, indicating that the particle is accelerating.
- Among the options provided, the one that shows the particle moving in a helical path with increasing x-coordinates (x1 < x2 < x3) is the correct answer.
Conclusion
- The correct option is Option D, which illustrates the particle accelerating in the positive x-direction while moving in a helical path.
- The magnetic field (B) is directed along the negative x-axis.
- The electric field (E) is directed along the positive x-axis.
- The charged particle moves with a velocity (V) that is inclined at an angle (θ) with the vertical in the x-y plane.
- We can resolve this velocity into two components:
- Vertical Component (V_y): This is the component of velocity in the y-direction, given by Vy=Vcos(θ).
- Horizontal Component (V_x): This is the component of velocity in the x-direction, given by Vx=Vsin(θ).
- The particle experiences a magnetic force due to the magnetic field. The magnetic force (F_m) is given by:
Fm=q(Vy×B)
where q is the charge of the particle and B is the magnetic field strength. Since the magnetic field is along the negative x-axis, the force will act in a direction perpendicular to both the velocity and the magnetic field.
- The particle also experiences an electric force (F_e) due to the electric field, which is given by:
Fe=qE
This force acts in the positive x-direction.
- The component of velocity perpendicular to the magnetic field (V_y) will cause the particle to move in a circular path due to the magnetic force.
- The electric field will exert a constant force in the positive x-direction, resulting in an acceleration in that direction.
- The combination of circular motion due to the magnetic field and linear acceleration due to the electric field results in a helical path.
- As the particle accelerates in the x-direction, the radius of the circular motion remains constant, but the pitch of the helix increases.
- The correct diagram should show a helical path that is increasing in the x-direction, indicating that the particle is accelerating.
- Among the options provided, the one that shows the particle moving in a helical path with increasing x-coordinates (x1 < x2 < x3) is the correct answer.
- The correct option is Option D, which illustrates the particle accelerating in the positive x-direction while moving in a helical path.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Multiple Correct34videos
MISCELLANEOUS VOLUME 5
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Linked Comprehension84videos
MISCELLANEOUS VOLUME 5
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False3videos
MISCELLANEOUS VOLUME 3
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - ddp.5.514videos
NUCLEAR PHYSICS
Similar Questions
Equipotential surfaces associated with a uniform electric field along positive x-axis are planes parallel to
View SolutionThere exist uniform magnetic and electric fields of manitudes 1T and 1Vm−1 respectively, along positive y-axis. A charged particle of mass 1kg and charge 1C is having velocity 1ms−1 along x-axis and is at origin at t=0. Then, the coordinates of the particle at time πs will be
View SolutionThere exist uniform magnetic and electric fields of manitudes 1T and 1Vm−1 respectively, along positive y-axis. A charged particle of mass 1kg and charge 1C is having velocity 1ms−1 along x-axis and is at origin at t=0. Then, the coordinates of the particle at time πs will be
View SolutionA particle of mass m and charge q is lying at the origin in a uniform magnetic field B directed along x-axis. At time t = 0, it is given a velocity v0, at an angleθ with the y-axis in the xy-plane. Find the coordinates of the particle after one revolution.
View SolutionAn electron is moving along positive x-axis. To get it moving on an anticlockwise circular path in x-y plane, a magnetic field is applied
View SolutionAn electron is moving along positive x-axis. To get it moving on an anticlockwise circular path in x-y plane, a magnetic field is applied
View SolutionA positively charged particle, having charge q, is accelerated by a potential difference V. This particle moving along the x-axis enters a region where an electric field E exists. The direction of the electric field is along positive y-axis. The electric field exists in the region bounded by the lines x=0andx=a. Beyond the line x=a (i.e., in the region x>a), there exists a magnetic field of strength B, directed along the positive y-axis. Find

a. at which point does the particle meet the line x=a.
b. the pitch of the helix formed after the particle enters the region x≥a. (Mass of the particle is m.)View SolutionA proton is moving along the negative direction of X-axis in a magnetic field directed along the positive direction of Y-axis. The proton will be deflected along the negative direction of
View SolutionIn a certain region of space, there exists a uniform and constant electric field of magnitude E along the positive y-axis of a coordinate system. A charged particle of mass m and charge -q (qgt0) is projected form the origin with speed 2v at an angle of 60∘ with the positive x-axis in x-y plane. When the x-coordinate of particle becomes √3mv2/qE a uniform and constant magnetic field of strength B is also switched on along positive y-axis.
Velocity of the particle just before the magnetic field is switched on isView SolutionIn a certain region of space, there exists a uniform and constant electric field of magnitude E along the positive y-axis of a coordinate system. A charged particle of mass m and charge -q (qgt0) is projected form the origin with speed 2v at an angle of 60∘ with the positive x-axis in x-y plane. When the x-coordinate of particle becomes √3mv2/qE a uniform and constant magnetic. field of strength B is also switched on along positive y-axis.
x-coordinate of the particle as a function of time after the magnetic field is switched on isView Solution

