The magnitude of electric field →E in the annular region of a charged cylindrical capacitor.
is the same throughout
is higher near the outer cylinder than near the inner cylinder
varies as 1r2 where r is the distance from the axis
varies as 1r3 where r is the distance from the axis.
The correct Answer is:C
To find the magnitude of the electric field →E in the annular region of a charged cylindrical capacitor, we can follow these steps:
Step 1: Understand the Configuration
We have a cylindrical capacitor consisting of two concentric cylinders. The inner cylinder has a linear charge density λ and the outer cylinder is neutral or grounded. We will analyze the electric field in the annular region between the two cylinders.
Step 2: Apply Gauss's Law
To find the electric field, we can use Gauss's Law, which states:
ΦE=Qencϵ0
where ΦE is the electric flux through a closed surface, Qenc is the charge enclosed by that surface, and ϵ0 is the permittivity of free space.
Step 3: Choose a Gaussian Surface
We consider a cylindrical Gaussian surface of radius r (where r is greater than the radius of the inner cylinder) and length L. The electric field →E is uniform and radial at this surface.
Step 4: Calculate the Electric Flux
The electric flux through the curved surface of the cylinder is given by:
ΦE=E⋅A=E⋅(2πrL)
where A is the area of the curved surface of the cylinder.
Step 5: Determine the Enclosed Charge
The charge enclosed by the Gaussian surface is the charge on the inner cylinder:
Qenc=λL
where λ is the linear charge density.
Step 6: Apply Gauss's Law
Substituting the expressions for electric flux and enclosed charge into Gauss's Law, we get:
E⋅(2πrL)=λLϵ0
Step 7: Solve for the Electric Field
Now, we can solve for E:
E=λ2πϵ0r
This shows that the electric field E in the annular region is inversely proportional to the distance r from the axis of the cylinder.
Final Expression
Thus, the magnitude of the electric field in the annular region of the charged cylindrical capacitor is:
E=λ2πϵ0r
We have a cylindrical capacitor consisting of two concentric cylinders. The inner cylinder has a linear charge density λ and the outer cylinder is neutral or grounded. We will analyze the electric field in the annular region between the two cylinders.
To find the electric field, we can use Gauss's Law, which states:
ΦE=Qencϵ0
where ΦE is the electric flux through a closed surface, Qenc is the charge enclosed by that surface, and ϵ0 is the permittivity of free space.
We consider a cylindrical Gaussian surface of radius r (where r is greater than the radius of the inner cylinder) and length L. The electric field →E is uniform and radial at this surface.
The electric flux through the curved surface of the cylinder is given by:
ΦE=E⋅A=E⋅(2πrL)
where A is the area of the curved surface of the cylinder.
The charge enclosed by the Gaussian surface is the charge on the inner cylinder:
Qenc=λL
where λ is the linear charge density.
Substituting the expressions for electric flux and enclosed charge into Gauss's Law, we get:
E⋅(2πrL)=λLϵ0
Now, we can solve for E:
E=λ2πϵ0r
This shows that the electric field E in the annular region is inversely proportional to the distance r from the axis of the cylinder.
Thus, the magnitude of the electric field in the annular region of the charged cylindrical capacitor is:
E=λ2πϵ0r
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - HOTS
5 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - EXEMPLAR PROBLEMS
3 Videos
- ELECTROMAGNETIC WAVESBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Assertion And Reason
15 Videos
- MAGNETISM AND MATTER BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - NCERT Exemplar
5 Videos
Similar Questions
How does the electric field (E) between the plates of a charged cylindrical capacitor vary with the distance r from the axis of the cylinder ?
View SolutionThe electric force experienced by a charge of 5×10−6C is 25×10−3N. Find the magnitude of the electric field at that position of the charge due to the source charges.
View SolutionShow that the force on each plate of a parallel plate capacitor has a magnitude equal to (½)QE, where Q is the charge on the capacitor, and E is the magnitude of electric field between the plates. Explain the origin of the factor ½.
View SolutionThe magnitude of the electric field on the surface of a sphere of radius r having a uniform surface charge density σ is
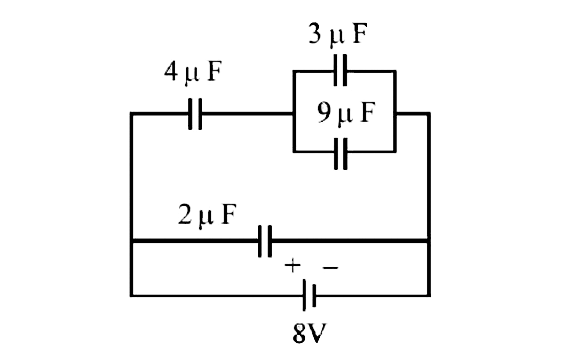
View SolutionA combination of capacitors is set up as shown in the figure. The magnitude of the electric field, due to a point charge Q (having a charge equal to the sum of the charges on the 4μF and 9μF capacitors), at a point distance 30 m from it, would equal:
View SolutionConisder a thin spherical shell of radius R with centre at the origin, carrying uniform poistive surface charge denisty. The variation of the magnitude of the electric field ∣∣→E(r)∣∣ and the electric potential V(r) with the distance r from the centre, is best represented by which graph?
View SolutionThe maximum electric field at a point on the axis of a uniformly charged ring is E0. At how many points on the axis will the magnitude of the electric field be E0/2.
View SolutionA charge q is uniformly distributed over a quarter circular ring of radius r. The magnitude of electric field strength at the centre of the ring will be
View SolutionEven though an electric field →E exerts a force q→E on a charged particle yet the electric field of an EM wave does not contribute to the radiation pressure (but transfer energy). Explain.
View SolutionA cylindrical region of radius R contains a uniform magnetic field parallel to axis with magnitude that is changing linearly with time. If r is the radial distance of a point from axis of cylinder in a plane perpendicular to axis then the magnitude of the induced electrical field outside the cylinder is directly proportional to
View Solution
