The magnituge of 'B' from a conductor carrying 35A at a perpendicular distance of 20cm from it, in tesla is
3.5×10−5
3.5×10−3
0.315×10−5
0.035×10−5
The correct Answer is:A
To find the magnitude of the magnetic field B at a perpendicular distance from a straight conductor carrying current, we can use the formula:
B=μ0I2πr
where:
- B is the magnetic field in tesla (T),
- μ0 is the permeability of free space (4π×10−7T m/A),
- I is the current in amperes (A),
- r is the distance from the conductor in meters (m).
1. Identify the given values:
- Current I=35A
- Distance r=20cm=0.2m
2. Substitute the values into the formula:
B=μ0I2πr=4π×10−7T m/A×35A2π×0.2m
3. Simplify the expression:
- The π in the numerator and denominator cancels out:
B=4×10−7×352×0.2
4. Calculate the denominator:
2×0.2=0.4
5. Now substitute back into the equation:
B=4×35×10−70.4
6. Calculate 4×35:
4×35=140
7. Now substitute this value back:
B=140×10−70.4
8. Divide 140 by 0.4:
140÷0.4=350
9. Now we have:
B=350×10−7T
10. Convert 350×10−7 to scientific notation:
B=3.5×10−5T
Final Answer:
The magnitude of the magnetic field B at a perpendicular distance of 20 cm from the conductor carrying 35 A is:
B=3.5×10−5T
- B is the magnetic field in tesla (T),
- μ0 is the permeability of free space (4π×10−7T m/A),
- I is the current in amperes (A),
- r is the distance from the conductor in meters (m).
- Current I=35A
- Distance r=20cm=0.2m
B=μ0I2πr=4π×10−7T m/A×35A2π×0.2m
- The π in the numerator and denominator cancels out:
B=4×10−7×352×0.2
2×0.2=0.4
B=4×35×10−70.4
4×35=140
B=140×10−70.4
140÷0.4=350
B=350×10−7T
B=3.5×10−5T
The magnitude of the magnetic field B at a perpendicular distance of 20 cm from the conductor carrying 35 A is:
B=3.5×10−5T
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-III49videos
MOVING CHARGES AND MAGNETISM
- BOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-IB71videos
MOVING CHARGES AND MAGNETISM
- BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - very Short answer type question15videos
MOTION IN A STRAIGHT LINE
- BOOK - AAKASH SERIESCHAPTER - NUCLEAR PHYSICSEXERCISE - ADDITIONAL PRACTICE PRACTICE SHEET (ADVANCED) Integer Type Questions3videos
NUCLEAR PHYSICS
Similar Questions
A straight conductor of length 32 cm carries a current of 30A. Magnetic induction at a point which is in air at a perpendicular distance of 12cm from the mid point of the conductor is
View SolutionA current 'I' flows along an infinitely long straight conductor. If 'r' is the perpendicular distance of a point from the lower end of the conductor, then the magnetic induction B is given by
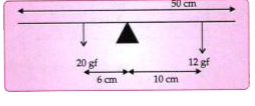
View SolutionA half metre rod is pivoted at the centre with two weights of 20 gf and 12 gf suspended at a perpendicular distance of 6 cm and 10 cm from the pivot respectively as shown below:
Is the rod in equilibrium ?View SolutionFind the magnetic induction due to a straight conductor of length 16cm carrying current of 5A at a distance of 6cm from the midpoint of conductor
View Solution4×1010 electrons are removed from a neutral metal sphere of diameter 20 cm placed in air. The magnitude of the electric field (in NC−1) at a distance of 20 cm from its centre is
View SolutionUsing Ampere.s circuital law, obtain an expression for the magnetic flux density .B. at a point .X. at a perpendicular distance .r. from a long current carrying conductor. (Statement of the law is not required).
View SolutionThe straight long conductors AOB and COD are perpendicular to each other and carry current i1 and i2. The magnitude of the magnetic induction at point P at a distance a from the point O in a direction perpendicular to the plane ACBD is
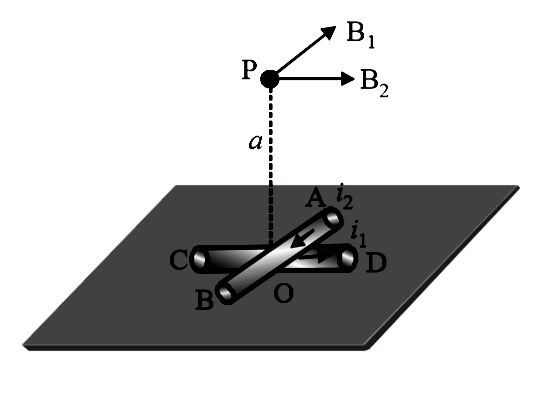 View Solution
View SolutionThe straight long conductors AOB and COD are perpendicular to each other and carry current i1 and i2. The magnitude of the magnetic induction at point P at a distance a from the point O in a direction perpendicular to the plane ACBD is
 View Solution
View SolutionUsing Ampere 's circuital law or Biot- Savart's a law, show that magnetic flux density B at point P at a perpendicular distance a from a long current carrying conductor is given by B=(μ4π)2Ia [ Statement of the laws not required]
View SolutionA square loop, carrying a steady current I, is placed in a horizontal plane near a long staright conductor carryinf a steady current I, at a distance d from the conductor as shown in Fig. The loop wil experience
 View Solution
View Solution

