The maximum tensoin that an inextensible ring of radius 1 m and mass density 0.1 kg m−1 can bear is 40 N. The maximum angular velocity with which it can be rotated in a circular path is
20 rad s−1
16 rad s−1
18 rad s−1
15 rad s−1
The correct Answer is:A
To find tension in the ring, let us take an arc which subtends angle 2(dθ) at centre. Tangential components of T cancel out each other, while inward components provide the necessary centripetal force. Thus,
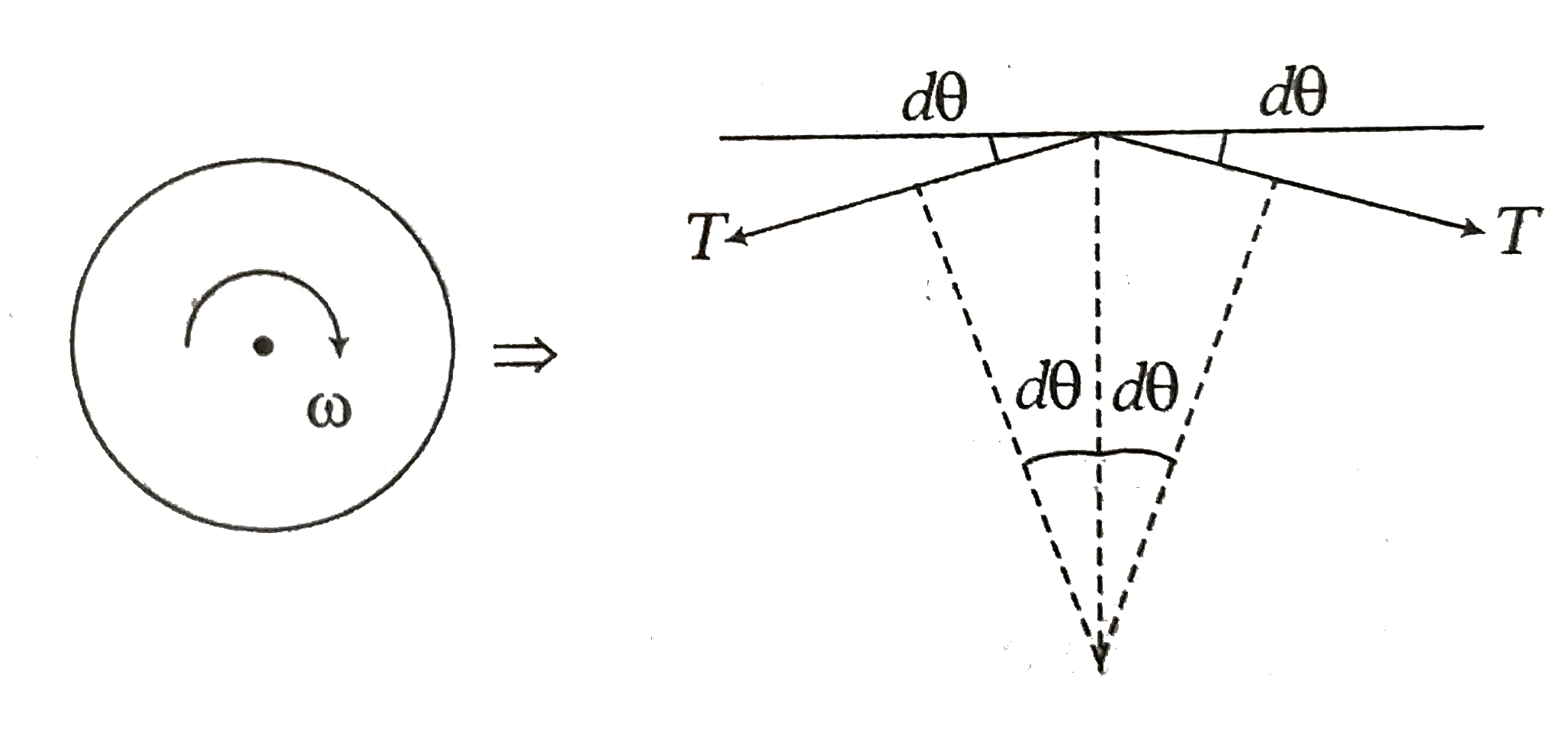
2Tsin(dθ)=(dm)rω2=(λ2R.dθ)(Rω2)
Here, λ→ linear mass density.
For small angles, sindθ≈dθ
∴ 2Tdθ=2λR2ω2dθ or T=λR2ω2
ωmax=√Tmaxλ.1R=√400.1×11=20rad s−1)
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Match the columns
3 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery
19 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Check point
45 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct
27 Videos
Similar Questions
A bob of mass 10 kg is attached to wire 0.3 m long. Its breaking stress is 4.8×107N/m2. The area of cross section of the wire is 10−6m2. The maximum angular velocity with which it can be rotated in a horizontal circle
View SolutionA bob of mass 10kg is attached to a wire 0.3m long. Its breaking stress is 4.8×107N/m2. Then area of cross-section of the wire is 10−6m2. What is the maximum angular velocity with which it can be rotated in a horizontal circle?
View SolutionA bob of mass 10 kg is attached to wire 0.3 m long. Its breaking stress is 4.8×107N/m2. The area of cross section of the wire is 10−6m2. The maximum angular velocity with which it can be rotated in a horizontal circle
View SolutionA ring of radius 'r' and mass per unit length 'm' rotates with an angular velocity 'ω' in free space then tension will be :
View SolutionA particle of mass 100 g tied to a string is rotated along the circle of radius 0.5 m. The breaking tension of the string is 10 N. The maximum speed with which particle can be rotated without breaking the string is
View SolutionA ring of radius 0.5 m and mass 10 kg is rotating about its diameter with angular velocity of 20rads−1. Its kinetic energy is
View SolutionA body of mass m = 10 kg is attached to a wire of length 0.3m. The maximum angular velocity with which it can be rotated in a horizontal circle is (Given, breaking stress of wire =4.8×107Nm−2 and area of cross-section of a wire =10−6m2)
View Solution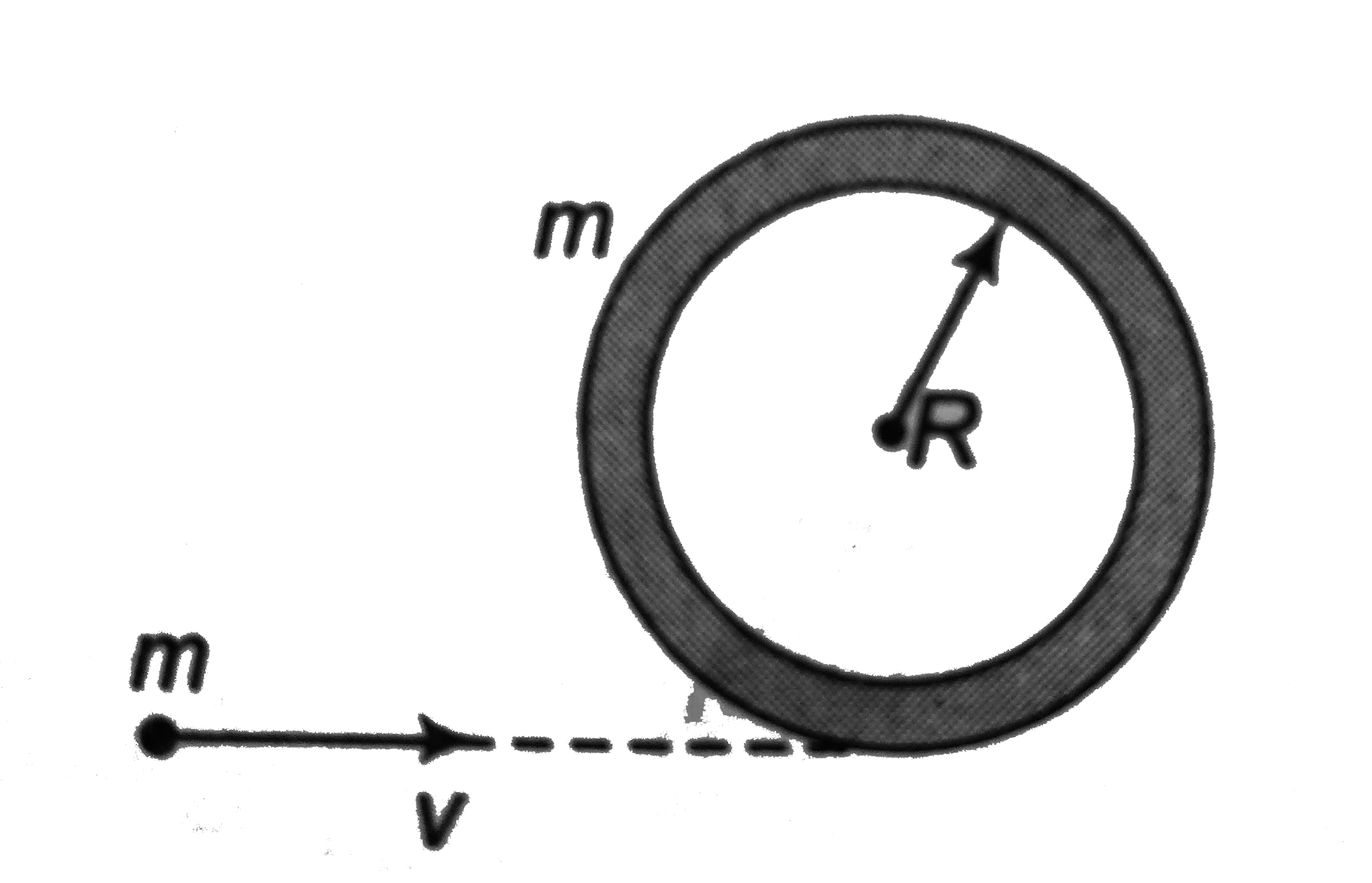
A circular ring of mass m and radius R rests flat on a horizontal smooth surface as shown in figure. A particle of mass m, and moving with a velocity v. Collides inelastically (e=0) with the ring the angular velocity with which the system rotates after the particle strikes the ring is
View SolutionA ring of mass m and radius R is being rotated about its axis with angular velocity o. If o increases then tension in ring
View SolutionA ball of mass (m)0.5kg is attached to the end of a string having length (L)0.5m. The ball is rotated on a horizontal circular path about vertical axis. The maximum tension that the string can bear is 324N. The maximum possible value of angular velocity of ball (in radian//s) is -
 .
.
View Solution
