The oscillation of a body on a smooth horizental surface is respresented by the equation
X=Acos(ωt)
where one of the following graph shown correctly the variation a with t?
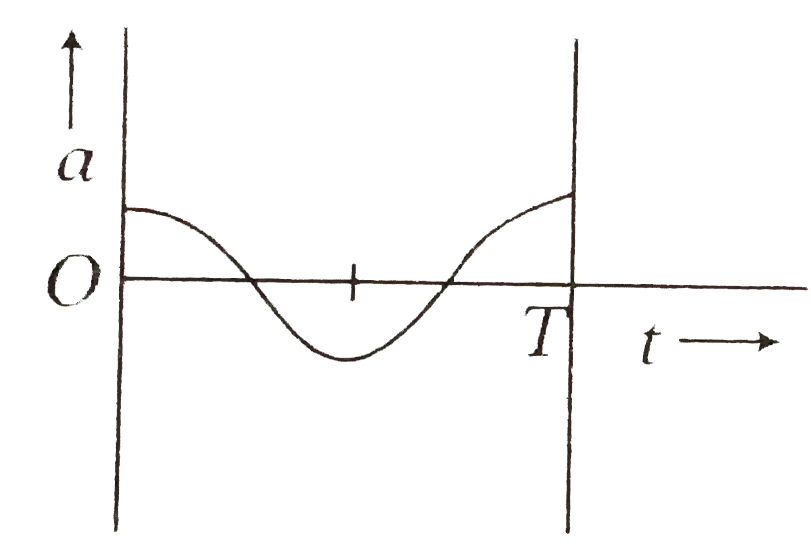
The correct Answer is:C
To solve the problem, we need to analyze the given displacement equation and derive the acceleration from it. Here’s a step-by-step breakdown:
Step 1: Understand the Displacement Equation
The displacement of the body is given by the equation:
x=Acos(ωt)
where:
- x is the displacement,
- A is the amplitude,
- ω is the angular frequency,
- t is the time.
Step 2: Find the Velocity
The velocity v is the rate of change of displacement with respect to time. We can find it by differentiating the displacement equation with respect to t:
v=dxdt=−Aωsin(ωt)
Step 3: Find the Acceleration
The acceleration a is the rate of change of velocity with respect to time. We can find it by differentiating the velocity equation:
a=dvdt=−Aω2cos(ωt)
Step 4: Analyze the Acceleration Equation
The acceleration equation is:
a=−Aω2cos(ωt)
This indicates that the acceleration is proportional to the cosine function, but with a negative sign.
Step 5: Graph the Acceleration
The graph of −cos(ωt) will start at its maximum negative value when t=0 (since cos(0)=1), and it will oscillate between −Aω2 and Aω2. The graph will have the following characteristics:
- It will be a cosine wave.
- It will be inverted (negative cosine).
Step 6: Identify the Correct Graph
From the options provided, we need to identify the graph that represents the negative cosine function. The correct graph will start at the lowest point (minimum value) and will oscillate upwards and downwards, matching the behavior of −cos(ωt).
Conclusion
The correct option that represents the variation of acceleration with time is the one that shows a negative cosine wave.
---
The displacement of the body is given by the equation:
x=Acos(ωt)
where:
- x is the displacement,
- A is the amplitude,
- ω is the angular frequency,
- t is the time.
The velocity v is the rate of change of displacement with respect to time. We can find it by differentiating the displacement equation with respect to t:
v=dxdt=−Aωsin(ωt)
The acceleration a is the rate of change of velocity with respect to time. We can find it by differentiating the velocity equation:
a=dvdt=−Aω2cos(ωt)
The acceleration equation is:
a=−Aω2cos(ωt)
This indicates that the acceleration is proportional to the cosine function, but with a negative sign.
The graph of −cos(ωt) will start at its maximum negative value when t=0 (since cos(0)=1), and it will oscillate between −Aω2 and Aω2. The graph will have the following characteristics:
- It will be a cosine wave.
- It will be inverted (negative cosine).
From the options provided, we need to identify the graph that represents the negative cosine function. The correct graph will start at the lowest point (minimum value) and will oscillate upwards and downwards, matching the behavior of −cos(ωt).
The correct option that represents the variation of acceleration with time is the one that shows a negative cosine wave.
Similar Questions
Knowledge Check
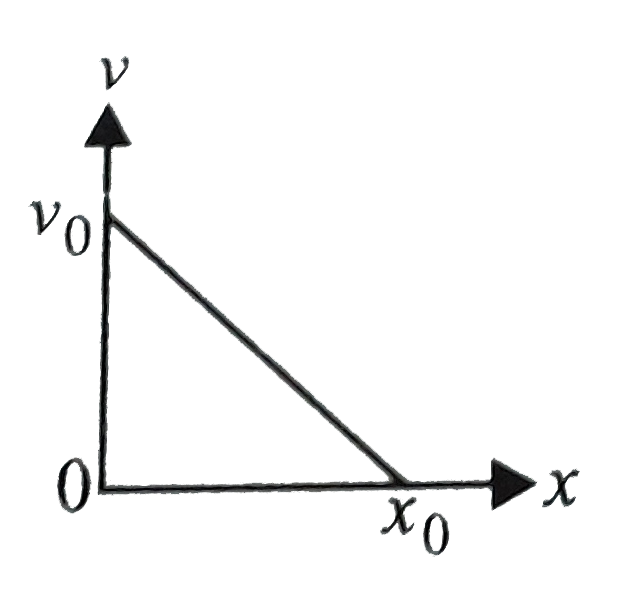
The velocity -displacement graph of a particle is as shown in the figure. Which of the following graphs correctly represents the variation of acceleration with displacement?
 A
A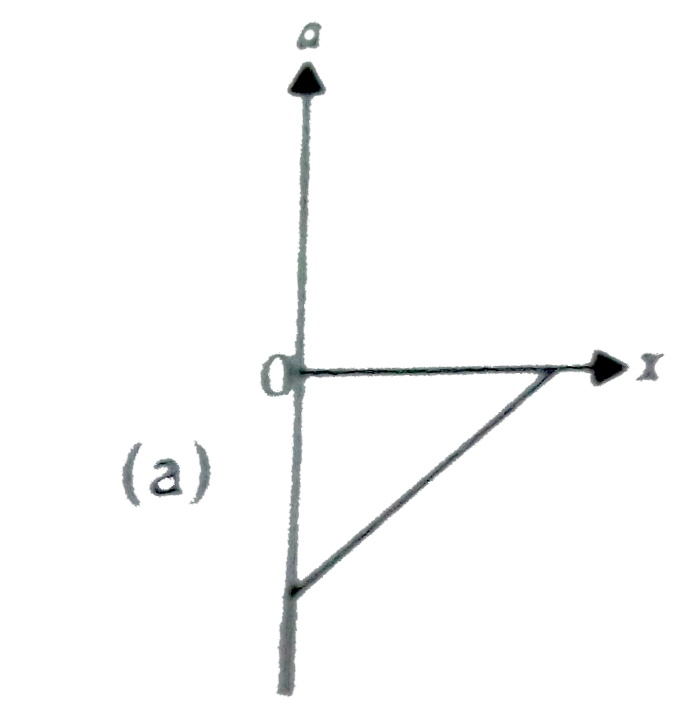 B
B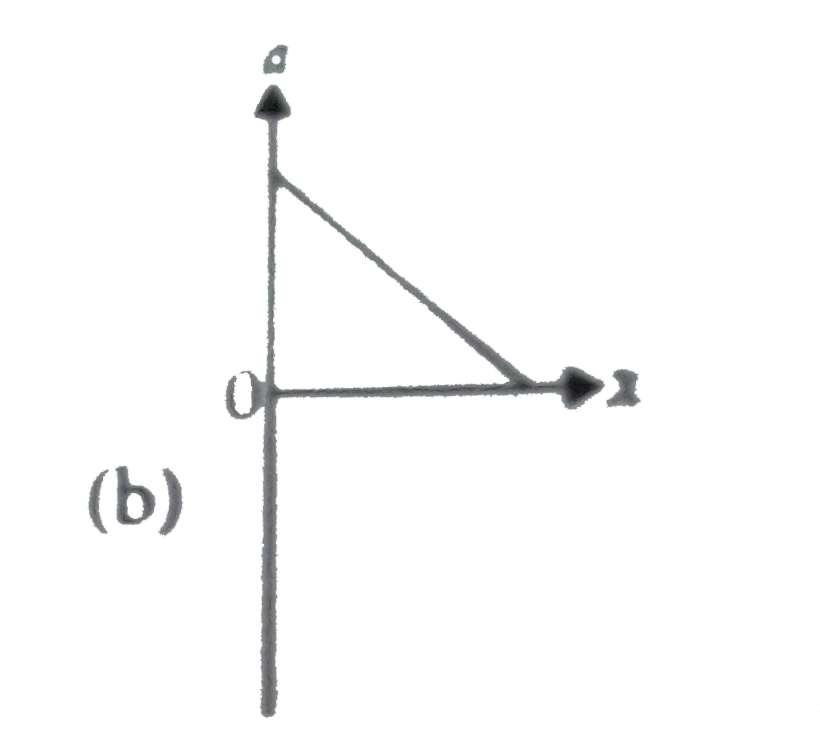 C
C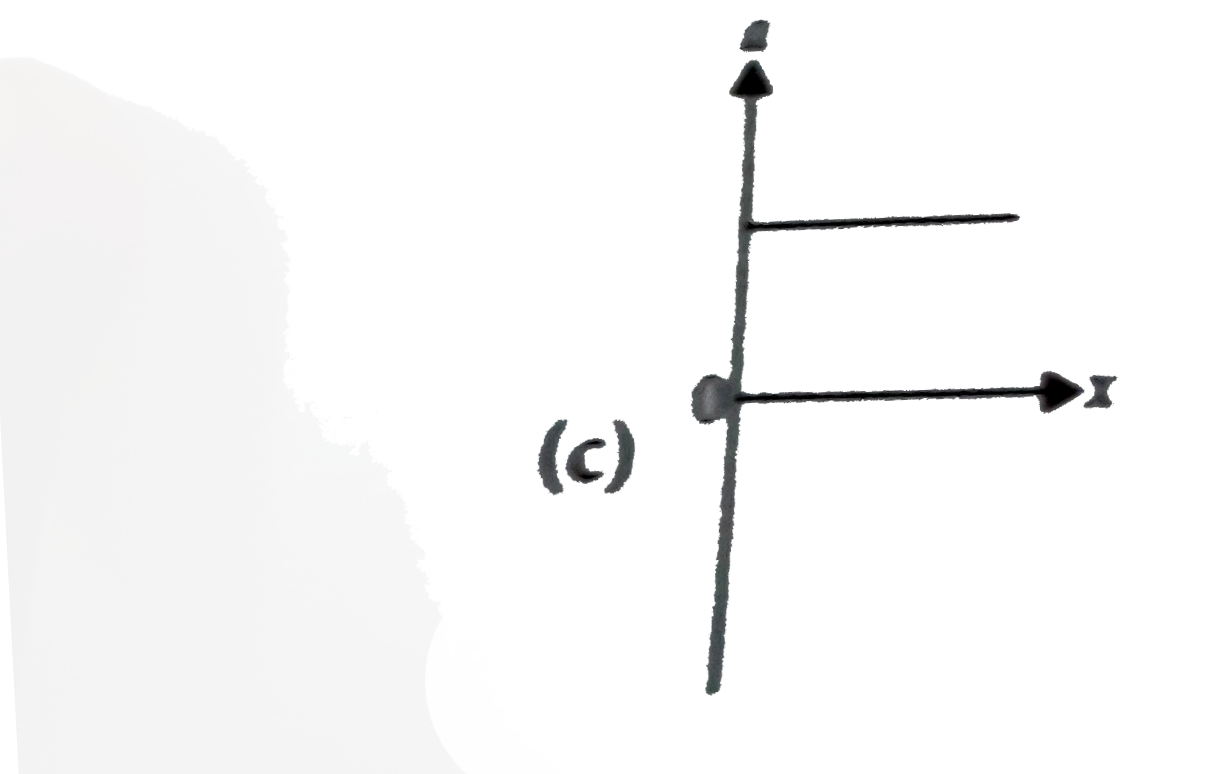 D
D
An alternating current I in an inductance coil varies with time t according to the graph as shown: Which one of the following graph gives the variation of voltage with time?
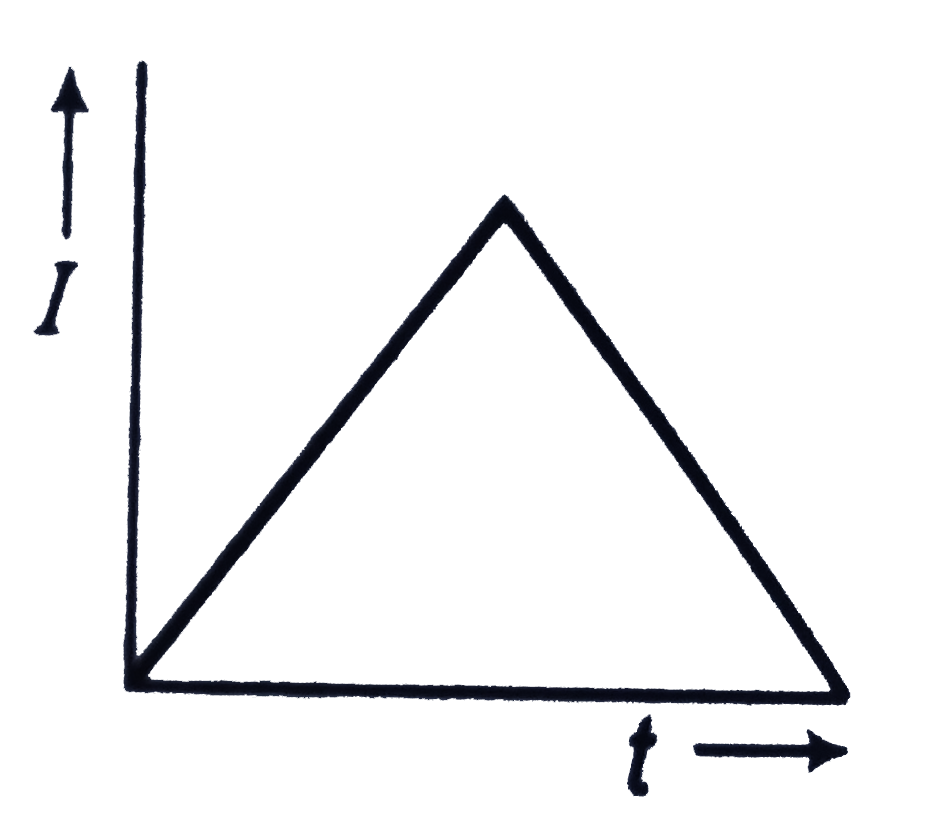
View SolutionAn alternating current I in an inductance coil varies with time t according to the graph as shown: Which one of the following graph gives the variation of voltage with time?

View SolutionA bob of mass m is connected by string of length L to point P. The system is released from rest with the pendulum bob in a horizontal position. Which of the following graph is correctly showing the variation of T (tension) with Ɵ?
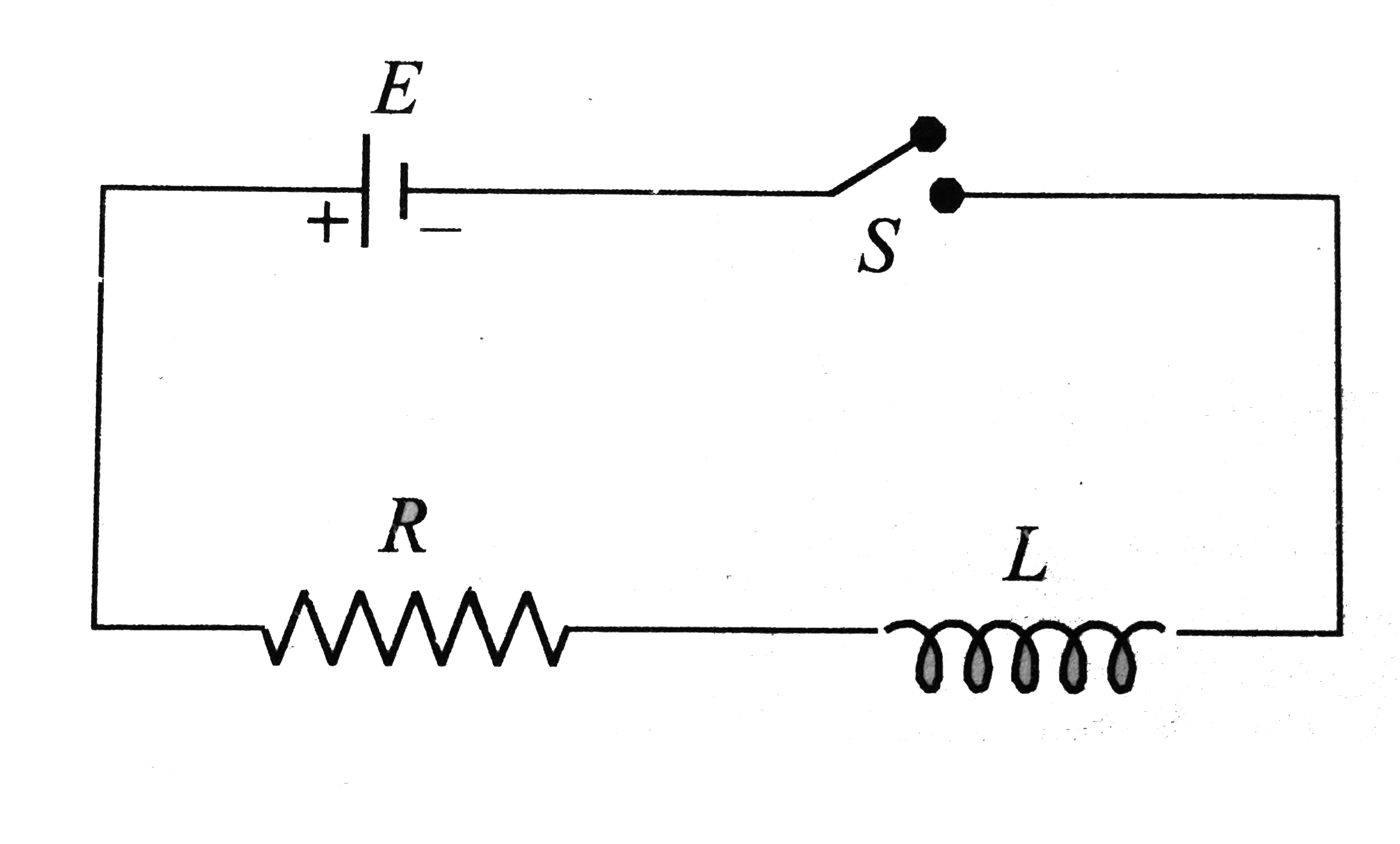
View SolutionSwitch S of the circuit shows in Fig. is closed at t=0. If e denotes the induced emf in L and i the current flowing through the circuit at time t, then which of the following graphs correctly represents the variation of e with i?
View SolutionThe velocity v of a particle moving along x - axis varies with ist position (x) as v=α√x, where α is a constant. Which of the following graph represents the variation of its acceleration (a) with time (t)?
View SolutionThe displacement x of a body of mass 1 kg on a horizontal smooth surface as a function of time t is given by x=t44. The work done in the first second is
View SolutionThe graph shown the variation with times t of the velocity v of an object . Which one of the following graphs best represents the variation of acceleration a of the object with time t?
View Solution
