The pendulum of a clock is replaced by a spring mass system with the spring having spring constant 0.1Nm−1. What mass should be attached to the spring?
The correct Answer is:=0.01kg≈10gm
To solve the problem, we need to determine the mass that should be attached to the spring in a spring-mass system, given that the spring constant k is 0.1N/m.
1. Understand the relationship between time period and mass:
The time period T of a spring-mass system is given by the formula:
T=2π√mk
where:
- T is the time period,
- m is the mass attached to the spring,
- k is the spring constant.
2. Rearranging the formula:
To find the mass m, we can rearrange the formula:
m=T2k4π2
Here, we need to know the time period T of the pendulum to proceed.
3. Assuming a time period:
For a typical pendulum clock, the time period is often around 1s. We will use this value for our calculations. Thus, T=1s.
4. Substituting the values:
Now we can substitute T=1s and k=0.1N/m into the rearranged formula:
m=(1)2⋅0.14π2
5. Calculating the mass:
First, calculate 4π2:
4π2≈39.478
Now substituting this value back into the equation:
m=0.139.478≈0.00254kg
6. Final result:
Therefore, the mass that should be attached to the spring is approximately:
m≈0.00254kg or 2.54grams
The time period T of a spring-mass system is given by the formula:
T=2π√mk
where:
- T is the time period,
- m is the mass attached to the spring,
- k is the spring constant.
To find the mass m, we can rearrange the formula:
m=T2k4π2
Here, we need to know the time period T of the pendulum to proceed.
For a typical pendulum clock, the time period is often around 1s. We will use this value for our calculations. Thus, T=1s.
Now we can substitute T=1s and k=0.1N/m into the rearranged formula:
m=(1)2⋅0.14π2
First, calculate 4π2:
4π2≈39.478
Now substituting this value back into the equation:
m=0.139.478≈0.00254kg
Therefore, the mass that should be attached to the spring is approximately:
m≈0.00254kg or 2.54grams
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:HC VERMAChapter:SIMPLE HARMONIC MOTIONExercise:Objective-2
Explore 2 Videos
- ROTATIONAL MECHANICSBook:HC VERMAChapter:ROTATIONAL MECHANICSExercise:Exercises
Explore 86 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBook:HC VERMAChapter:SOME MECHANICAL PROPERTIES OF MATTERExercise:Exercises
Explore 32 Videos
Similar Questions
Knowledge Check
Block is attached to system of springs. Calculate equivalent spring constant.
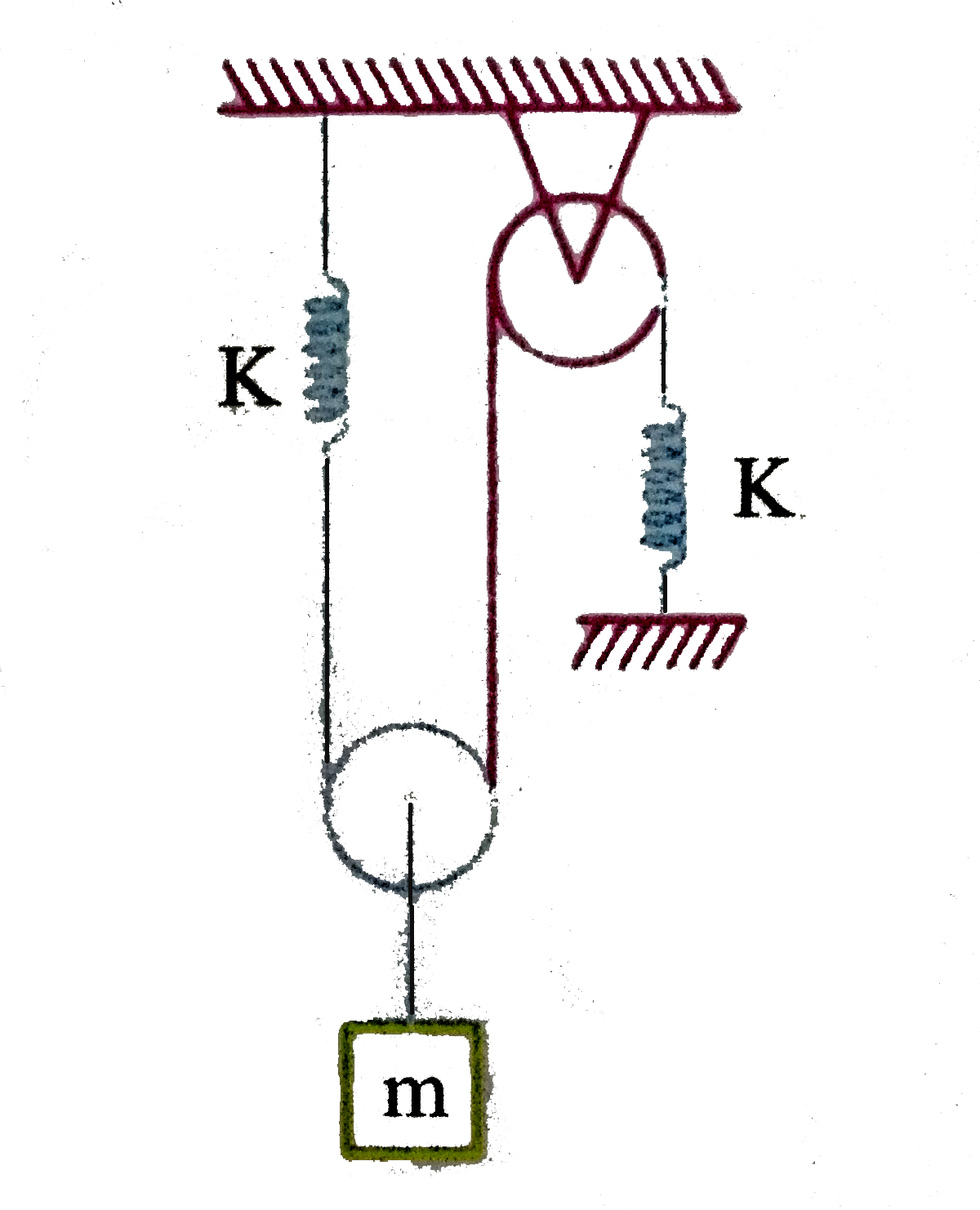 .AKB2KC3KD4K
.AKB2KC3KD4KFor a body of mass m attached to the spring the spring factor is given by
Am/ω2Bmω2Cm2ωDm2ω2A block of mass 2kg is attached with a spring of spring constant 4000Nm−1 and the system is kept on smooth horizontal table. The other end of the spring is attached with a wall. Initially spring is stretched by 5cm from its natural position and the block is at rest. Now suddenly an impulse of 4kg−ms−1 is given to the block towards the wall.
Find the velocity of the block when spring acquires its natural lengthA(a) 5ms−1B(b) 3ms−1C(c) 6ms−1D(d) None of these
Shm In Spring Mass System
View SolutionThe block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

View SolutionThe spring constant of the spring shown in the figure is 250Nm−1. Find the maximum compression of the spring?

View SolutionFor a spring-mass system spring having spring constant 19.7 N/m is attached to it. What should be the value of mass m (approx.) so that it will give the same period as that of seconds pendulum?
View SolutionA block A of mass 2 kg is connected with two springs, as shown . The spring constant of lower spring is system is thrice the spring costant of upper spring. The system is released from rest with both the springs unstreched. The maximum displacement of bloack is 0.1m. Find the acceleration of the block is its lowest position-
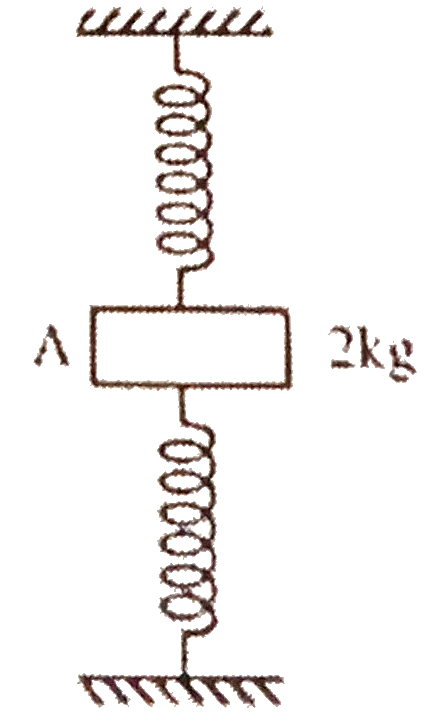
View Solution
