The planets with radii R1 and R2 have densities p1,p2 respectively. Their atmospheric pressues are p1 and p2 respectively.Therefore, the ratio of masses of their atmospheres, neglecting variation of g within the limits of atmoshpere is
p1R2ρ1p2R1ρ2
p1R2ρ2p2R1ρ1
p1R1ρ1p2R2ρ2
p1R1ρ2p2R2ρ1
The correct Answer is:D
p=ρatmgh=m43π[(R+h)3−R]GMR2h
⇒p=m43πR3[(1+hR)3−1)×G43πR3l0R2×h
m43πR3[(1+3hh−1]×G43πRl0h (Here M=43πR3l0)
Here p=mGρ3R
=∴M∝pRρ
Topper's Solved these Questions
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Multiple Correct
24 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Assertion- Reasoning
13 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Subjective
15 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE
1 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
Similar Questions
Knowledge Check
The atmospheric pressure at earth surface is P1 and inside a mine is P2. They are related as :
AP1=P2BP1>P2CP1<P2DP2=0The radii of two planets are respectively R1andR2 and their densities are respectively ρ1andρ2.The ratio of the accelerations due to gravity at their surface is
AR1ρ2R2ρ1BR1ρ1R2ρ2Cρ1R22ρ2R21DR1R2ρ1ρ2
N2O4 is dissociated to 33% and 40% at total pressure P1andP2 atm respectively. Then the ratio P1/P2 is
View SolutionAssertion : In the given figure shown, p1=p2.
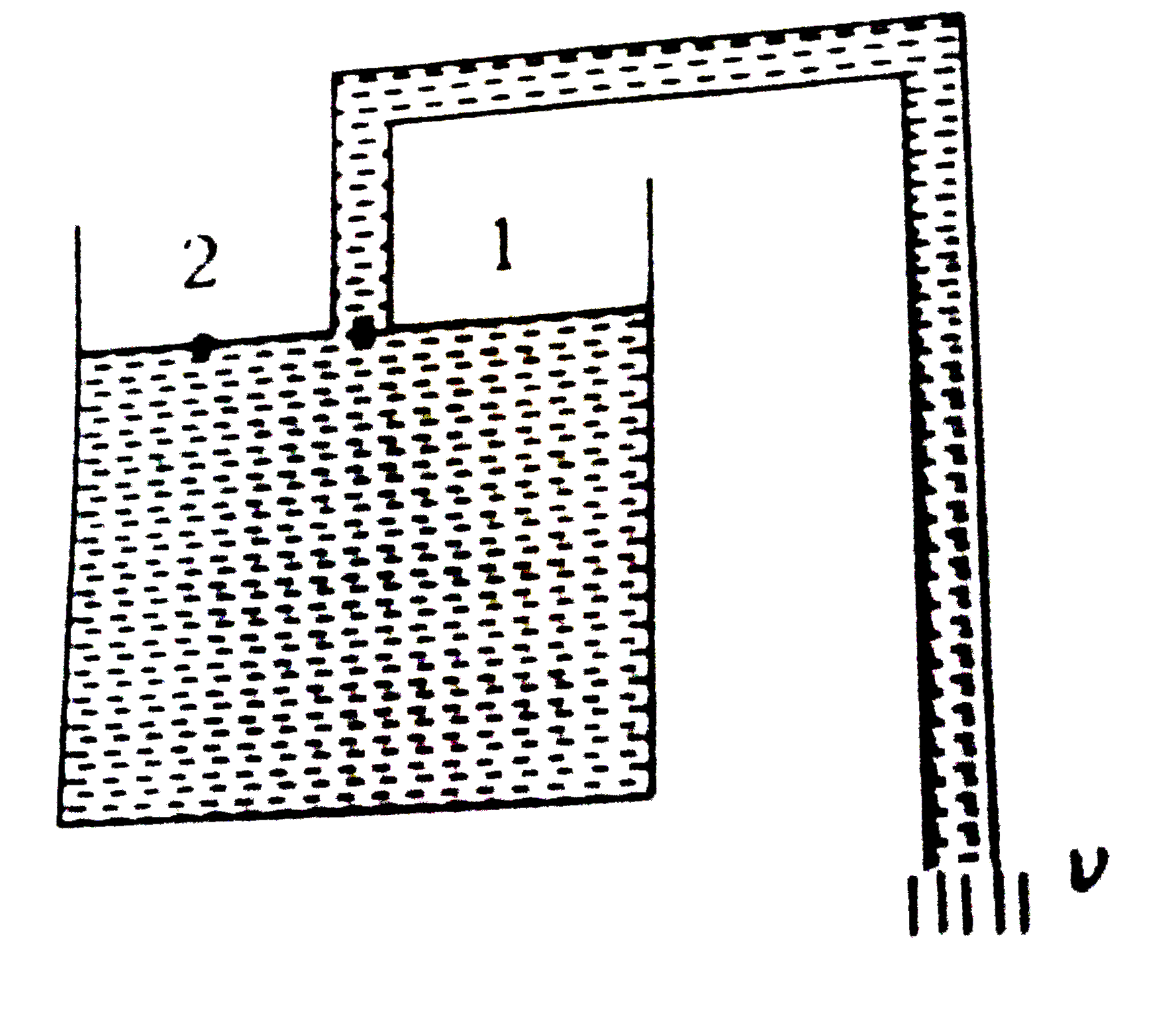
Reason : Pressure at 1 is less than the atmospheric pressure.
View SolutionIf p1,p2,p3 are respectively the perpendicular from the vertices of a triangle to the opposite sides, then find the value of p1p2p3.
View SolutionTwo concentric spherical shells of masses and radii m1,r1andm2,r2 respectively are as shown. The gravitational field intensity at point P is

View SolutionThe ratio of the radii of the planets P1andP2 is K1. the ratio of the acceleration due to gravity is K2. the ratio of the escape velocities from them will be
View SolutionTwo bodies with masses m1kgandm2kg have equal kinetic energies. If p1andP2 are their respective momenta, then p1/P2 is equal to :
View Solution