The pressure on an object of bulk modulus B undergoing hydraulic compression due to a stress exerted by surrounding fluid having volume strain (ΔVV)
B2(ΔVV)
B(ΔVV)2
1B(ΔVV)
B(ΔVV)
The correct Answer is:D
(d) B=Normal stressVolume strain=∣∣
∣
∣∣p−(ΔVV)∣∣
∣
∣∣=∣∣∣−pVV∣∣∣
p=VΔVV=B(ΔVV)
where, normal stress =p, volume strain =−ΔVV
Topper's Solved these Questions
Similar Questions
Define Bulk modulus of elasticity and write an expression in terms of pressure .P., volume .V. and change in volume .ΔV..
View SolutionA sound wave propagates in a medium of Bulk modulus B by means of compressions and rare fractions. If Pc and Pe are the pressures at compression and rarefaction respectively, .a. be the wave amplitude and k be the angular wave number then,
View Solution
Knowledge Check
An ideal gas is initially at temperature T and volume V. ITS volume is increased by ΔV due to an increase in temperature ΔT, pressure remaining constant. The quantity δ=ΔV/VΔT varies with temperature as
A B
B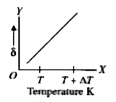 C
C D
D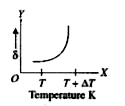
Two moles of an ideal monoatomic gas, initially at pressure p1 and volume V1, undergo an adiabatic compression until its volume is V2. Then the gas is given heat Q at constant volume V2.
(i) Sketch the complete process on a p-V diagram.
(ii) Find the total work done by the gas, the total change in its internal energy and the final temperature of the gas. [Give your answer in terms of p1,V1,V2,QandR]
View SolutionAn ideal gas is initially at temperature T and volume V. Its volume is increased by ΔV due to an increase in temperature ΔT, pressure remaining constant. The quantity δ=ΔVVΔT varies with temperature as
View SolutionA solid sphere of radius R made of a material of bulk modulus B is surrounded by a liquid in a cylindrical container. A massless piston of area A (the area of container is also A) floats on the surface of the liquid. When a mass M is placed on the piston to compress the liquid , fractional change in radius of the sphere is MgαAB. Find the value of α.
View SolutionIn the following questions, a statement of assertion is followed by a statement of reason. Mark the correct choice as
(a) If both assertion and reason are true and reason is the correct explanation of assertion.
(b) If both assertion and reason are true but reason is not the correct explanation of assertion.
(c ) If assertion is true but reason is false.
(d) If assertion and reason are false.
Q. Assertion: Bulk modulus of elasticity B represents incompressibility of the material
Reason: B=−△P△VV, where symbols have their usual meaning.
View SolutionThe strain energy stored in a body of volume V due to shear strain is ϕ (shear modulus is n)
View SolutionThree moles of an ideal gas (Cp=72R) at pressure p0 and temperature T0 is isothermally expanded to twice its initial volume. It is then compressed at a constant pressure to its original volume.
(a) Sketch p-V and p-T diagram for complete process.
(b) Calculate net work done by the gas.
(c) Calculate net heat supplied to the gas during complete process.
(Write your answer in terms of gas constant =R)
View SolutionA gaseous sample is generally allowed to do only expansion/compression type work against its surroundings The work done in case of an irreversible expansion ( in the intermediate stages of expansion/compression the states of gases are not defined). The work done can be calculated using
dw=−PextdV
while in case of reversible process the work done can be calculated using
dw=−PdV where P is pressure of gas at some intermediate stages. Like for an isothermal reversible process. Since P=nRTV, so
w=∫dW=−vf∫vinRTV.dV=−nRTln(VfVi)
Since dw=PdV so magnitude of work done can also be calculated by calculating the area under the PV curve of the reversible process in PV diagram.
If four identical samples of an ideal gas initially at similar state (P0,V0,T0) are allowed to expand to double their volumes by four different process.
I: by isothermal irreversible process
II: by reversible process having equation P2V= constant
III. by reversible adiabatic process
IV. by irreversible adiabatic expansion against constant external pressure.
Then, in the graph shown in the final state is represented by four different points then, the correct match can be
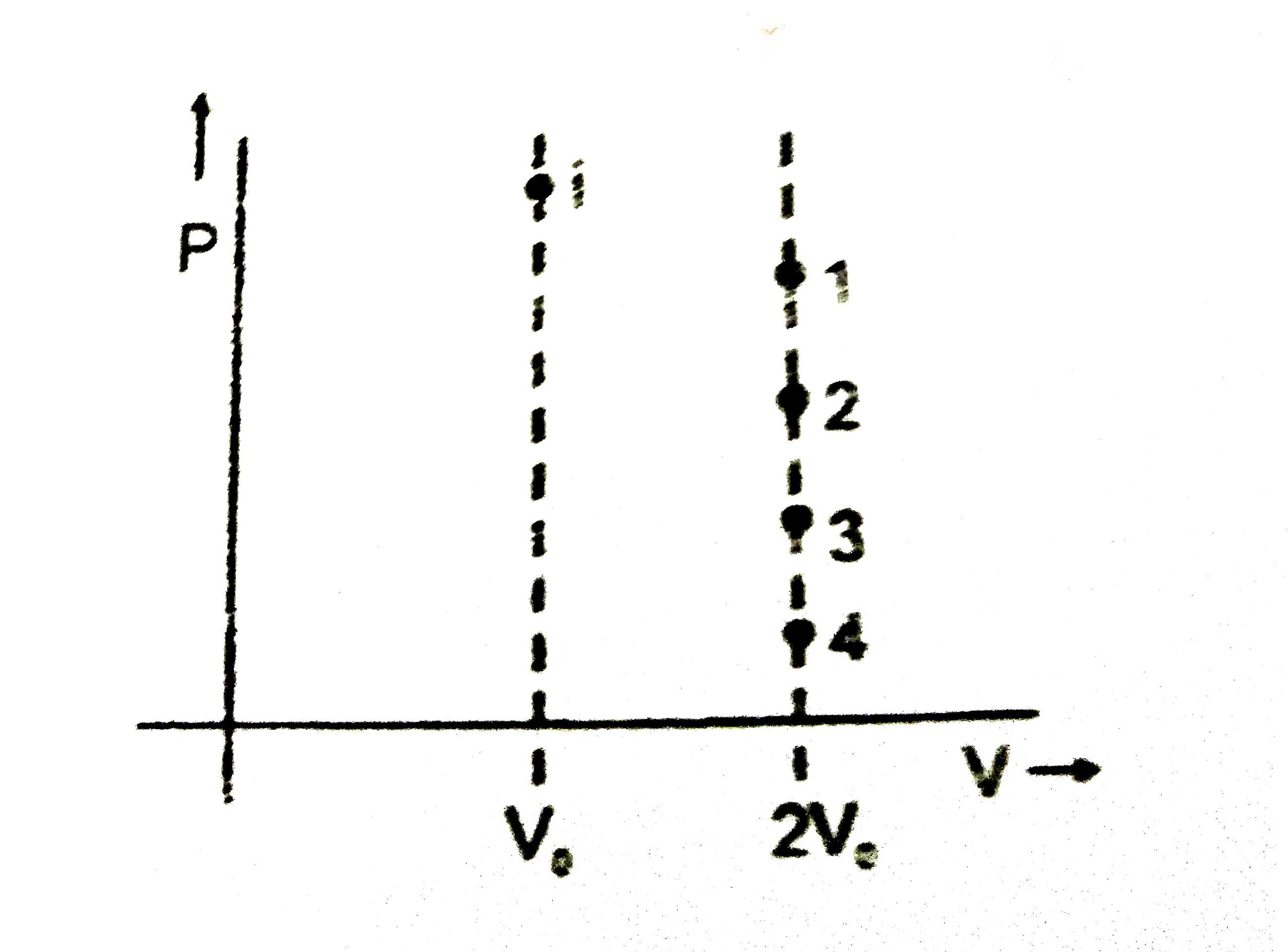
View Solution
