The resistance of a heater coil is 110Ω. A resistance R is connected in parallel with it and the combination is joined in series with a resistance of 11Ω to a 220V main line. The heater operates with a power of 110W. The value of R in Ω is
12.22
24.42
negative
that the given values are not correct
The correct Answer is:A
To solve the problem, we need to find the value of the resistance R that is connected in parallel with the heater coil. We will follow these steps:
Step 1: Identify the given values
- Resistance of heater coil, Rcoil=110Ω
- Series resistance, Rs=11Ω
- Total voltage, V=220V
- Power consumed by the heater, P=110W
Step 2: Calculate the current through the heater coil
Using the power formula:
P=I21⋅Rcoil
We can rearrange this to find I1:
I21=PRcoil=110110=1
Taking the square root:
I1=1A
Step 3: Determine the voltage across the heater coil
Since the heater operates at 1A:
Vcoil=I1⋅Rcoil=1⋅110=110V
Step 4: Calculate the voltage across the parallel combination
The total voltage is 220V and the voltage across the series resistance Rs is:
Vs=V−Vcoil=220−110=110V
Step 5: Find the total current in the circuit
Using Ohm's law, the total current I through the series circuit can be calculated as:
I=VRs+Rp
Where Rp is the equivalent resistance of the parallel combination of R and Rcoil.
Step 6: Set up the equation for the parallel resistance
The current through the parallel resistance R can be expressed as:
I2=VcoilR
And since I=I1+I2:
I=I1+I2=1+110R
Step 7: Substitute into the total current equation
We know that:
I=22011+Rp
Where Rp can be calculated as:
Rp=R⋅RcoilR+Rcoil
Step 8: Solve for R
Substituting Rp into the equation:
I=1+110R
And equating it to:
22011+R⋅110R+110
After manipulating and simplifying the equations, we will arrive at a quadratic equation in terms of R.
Step 9: Calculate the value of R
After solving the quadratic equation, we find:
R≈12.22Ω
Conclusion
The value of R is 12.22Ω.
---
- Resistance of heater coil, Rcoil=110Ω
- Series resistance, Rs=11Ω
- Total voltage, V=220V
- Power consumed by the heater, P=110W
Using the power formula:
P=I21⋅Rcoil
We can rearrange this to find I1:
I21=PRcoil=110110=1
Taking the square root:
I1=1A
Since the heater operates at 1A:
Vcoil=I1⋅Rcoil=1⋅110=110V
The total voltage is 220V and the voltage across the series resistance Rs is:
Vs=V−Vcoil=220−110=110V
Using Ohm's law, the total current I through the series circuit can be calculated as:
I=VRs+Rp
Where Rp is the equivalent resistance of the parallel combination of R and Rcoil.
The current through the parallel resistance R can be expressed as:
I2=VcoilR
And since I=I1+I2:
I=I1+I2=1+110R
We know that:
I=22011+Rp
Where Rp can be calculated as:
Rp=R⋅RcoilR+Rcoil
Substituting Rp into the equation:
I=1+110R
And equating it to:
22011+R⋅110R+110
After solving the quadratic equation, we find:
R≈12.22Ω
The value of R is 12.22Ω.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Calculating Thermal Power in Resistance14videos
HEATING EFFECT OF CURRENT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Integer Type4videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Concept Based8videos
INDUCTANCE
Similar Questions
Resistance of a Galvanometer coil is 8Ω and 2Ω Shunt resistance is connected with it. If main current is 1 A then the current flow through 2Ω resistance will be :
View SolutionA 100V voltmeter of internal resistance 20kΩ in series with a high resistance R is connected to a 110V line. The voltmeter reads 5V, the value of R is
View Solution
Knowledge Check
- Question 1 - Select One
When a resistance of 100Ω is connected in series with a galvanometer of resistance R, then its range is V. To double its range, a resistance of 1000Ω is connected in series. Find the value of R.
A1100B1000C900D800 - Question 2 - Select One
A heater is designed to operate with a power of 1000W in a 100V line. It is connected in combination with a resistance of 10Ω and a resistance R, to a 100V mains as shown in figure. What will be the value of R so that the heater operates with a power of 62.5W?
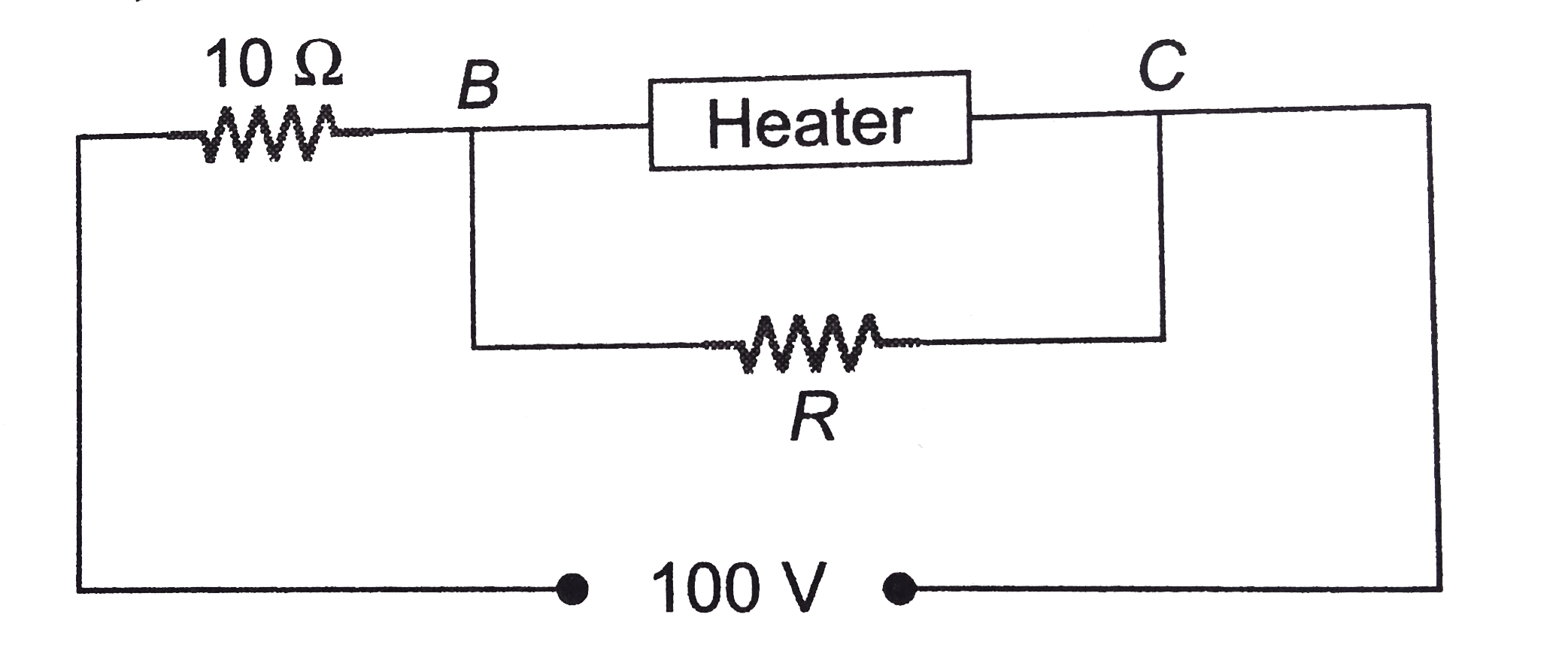 A15ΩB10ΩC5ΩD25Ω
A15ΩB10ΩC5ΩD25Ω
The Total resistance when connected in series in 9Ω and when connected in parallel is 2Ω The value of two resistance are
View SolutionWhen a resistance of 100Ω is connected in series with a galvanometer of resistance R, then its range is V. To double its range, a resistance of 1000Ω is connected in series. Find the value of R.
View SolutionThree resistors of 1Ω,2Ωand3Ω are connected in parallel. The combined resistance of 3 resistors should be
View SolutionTwo resistors of resistances 2Ω and 6Ω are connected in parallel. This combination is then connected to a battery of emf 2 V and internal resistance 0.5Ω. What is the current flowing through the battery ?
View SolutionTwo resistors having resistance 4 Ω and 6 Ω are connected in parallel. Find their equivalent resistance.
View SolutionA heater is designed to operate with a power of 1000W in a 100V line. It is connected in combination with a resistance of 10Ω and a resistance R, to a 100V mains as shown in figure. What will be the value of R so that the heater operates with a power of 62.5W?
 View Solution
View Solution

