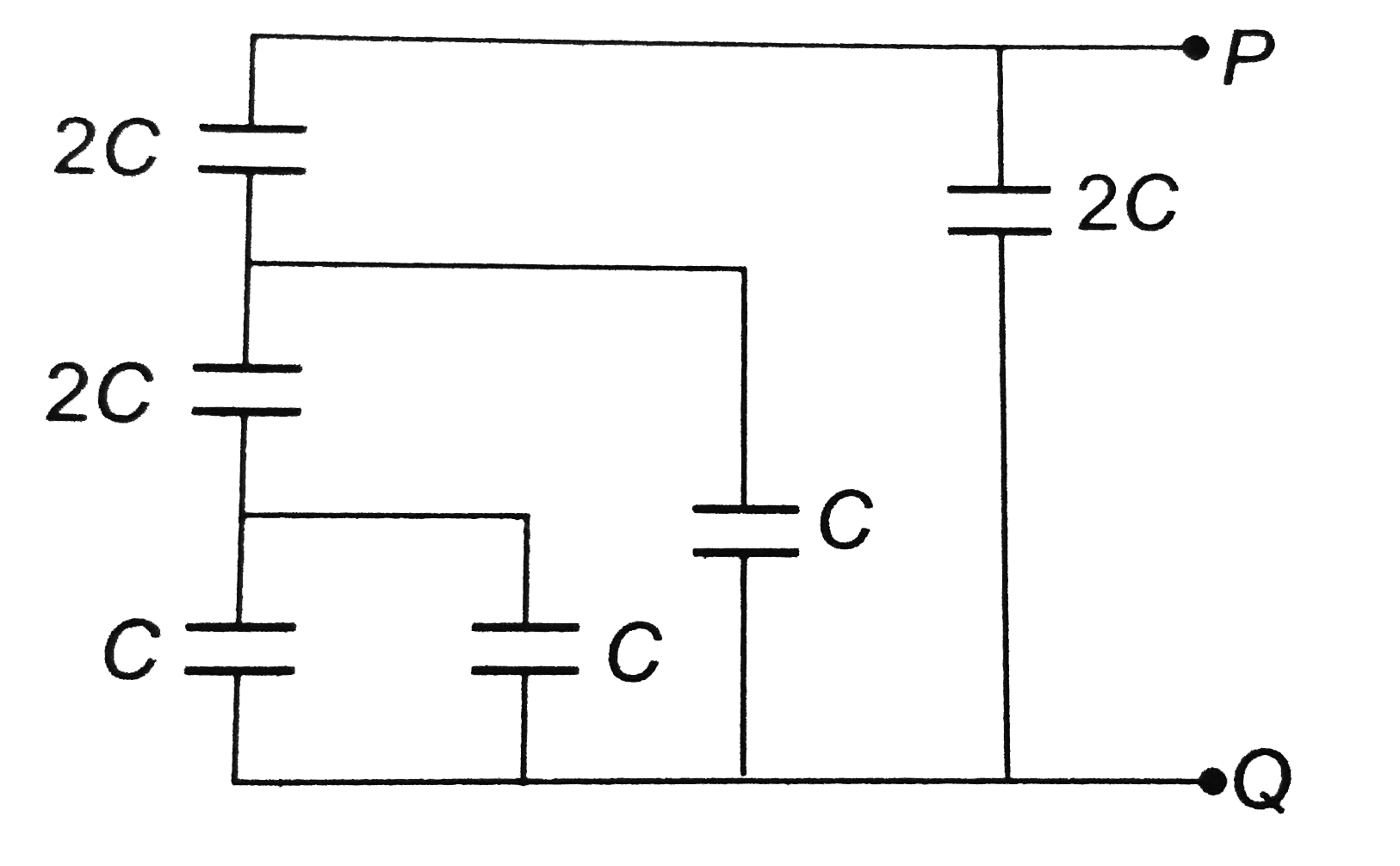
The resultant capacitance of given circuit between point P and Q is

2 µF
12 µF
3 µF
1 µF
The correct Answer is:A
Step by step video & image solution for The resultant capacitance of given circuit between point P and Q is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (B) Chapter exercises
17 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.5
20 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
The resultant capacitance of given circuit is
View SolutionFind the equivaent capacitance of the circuit between point A and B.
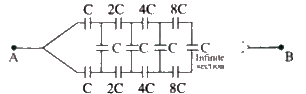
View SolutionThe equivalent capacitance of the circuit shown, between points A and B will be-

View SolutionFind the equivalent capacitance of the circuit between the points 'A' and 'B'. All capacitors are in microfarad.

View SolutionIn the circuit shown here, what is the value of the unknown resistor R so that the total resistance of the circuit between points P and Q is also equal to R

View SolutionThe capacitance of each capacitor as shown in the circuit is C. The effective capacitance of the circuit between terminals A and B is
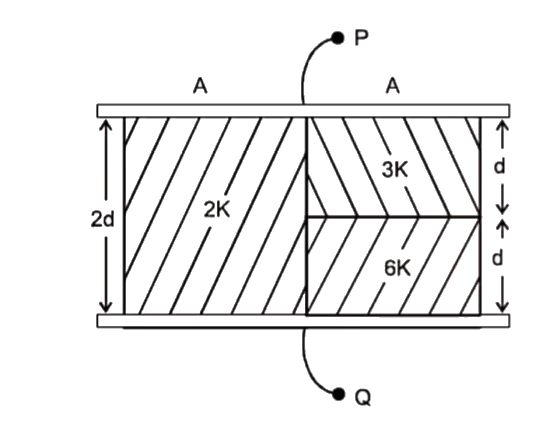
View SolutionThree different types of dielectric slabs have been arranged between the plates of a parallel plate capacitor, as shown in the figure. The equivalent capacitance of the system between the points P and Q will be
View SolutionEquivalent capacitance between points A and B is
_PHY_E05_281_Q01.png)
View SolutionThe equivalent capacitance between point A and B is
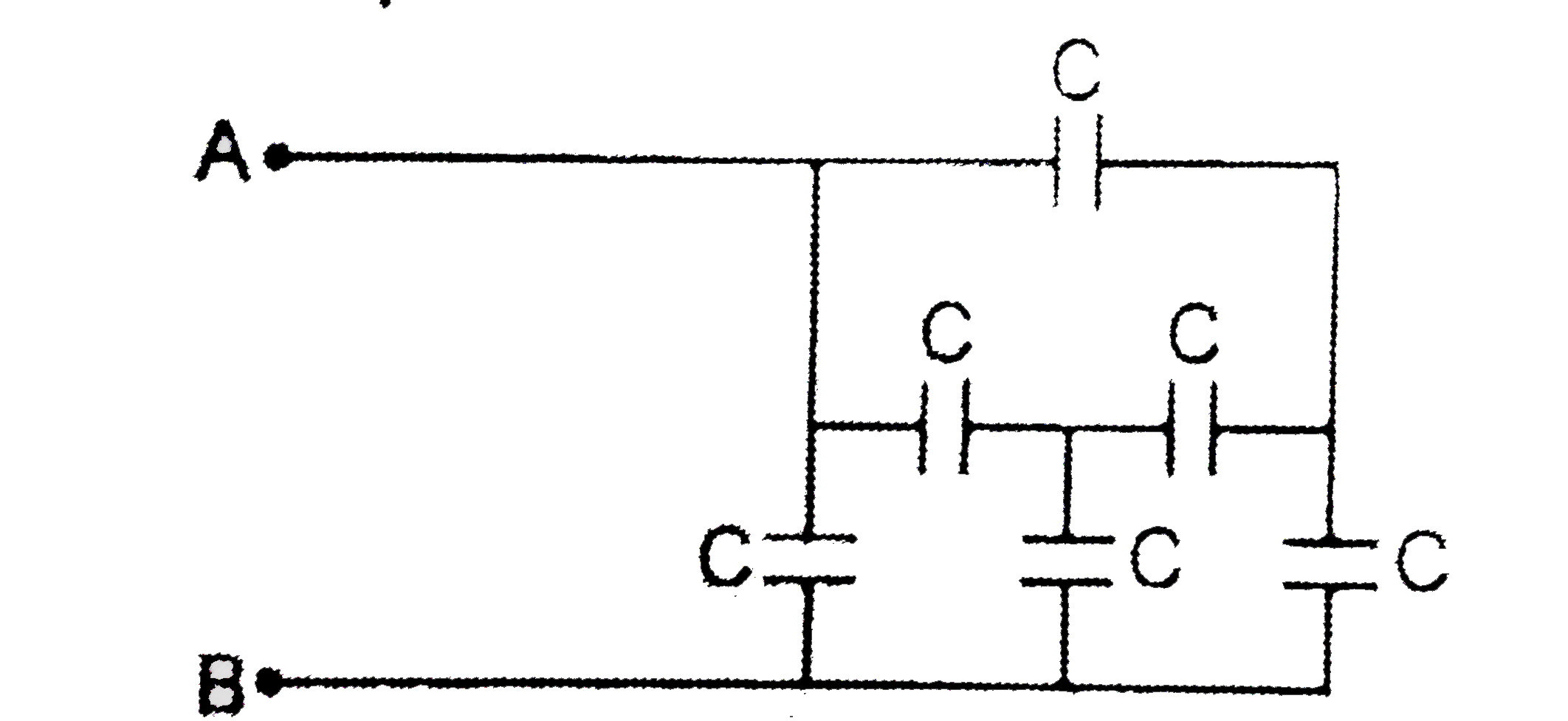
View SolutionThe resultant capacity between the points A and B in the adjoining circuit will be -

View Solution
