The scale of a galvanometer of resistance 100ohms contains 25 divisions. It gives a defelction of one division on passing a current of 4×10−4 amperes. The resistance in ohms to be added to it, so that it may become a voltmeter of range 2.5 volts is
150
170
110
220
The correct Answer is:A
To solve the problem, we need to determine the resistance to be added to a galvanometer to convert it into a voltmeter with a specified range. Here’s the step-by-step solution:
Step 1: Understand the given data
- Resistance of the galvanometer (G) = 100 ohms
- Number of divisions on the galvanometer scale = 25
- Current for 1 division = 4×10−4 A
- Voltage range of the voltmeter (V) = 2.5 V
Step 2: Calculate the maximum current (I_max) through the galvanometer
The maximum current that can be measured by the galvanometer when all divisions are used is:
Imax=Number of divisions×Current per division
Imax=25×4×10−4=100×10−4=10−2 A=0.01 A
Step 3: Write the formula for the voltmeter
When the galvanometer is converted into a voltmeter, the total voltage across the galvanometer and the added resistance (R) is given by:
V=I×Req
where Req=G+R (the total resistance in the circuit).
Step 4: Substitute known values into the formula
We know:
- V=2.5 V
- I=Imax=0.01 A
- G=100 ohms
Substituting these values into the voltage formula:
2.5=0.01×(100+R)
Step 5: Solve for R
First, rearranging the equation:
2.5=0.01×(100+R)
⇒2.5=1+0.01R
⇒2.5−1=0.01R
⇒1.5=0.01R
⇒R=1.50.01=150 ohms
Final Answer
The resistance to be added to the galvanometer to convert it into a voltmeter of range 2.5 volts is 150 ohms.
---
- Resistance of the galvanometer (G) = 100 ohms
- Number of divisions on the galvanometer scale = 25
- Current for 1 division = 4×10−4 A
- Voltage range of the voltmeter (V) = 2.5 V
The maximum current that can be measured by the galvanometer when all divisions are used is:
Imax=Number of divisions×Current per division
Imax=25×4×10−4=100×10−4=10−2 A=0.01 A
When the galvanometer is converted into a voltmeter, the total voltage across the galvanometer and the added resistance (R) is given by:
V=I×Req
where Req=G+R (the total resistance in the circuit).
We know:
- V=2.5 V
- I=Imax=0.01 A
- G=100 ohms
2.5=0.01×(100+R)
First, rearranging the equation:
2.5=0.01×(100+R)
⇒2.5=1+0.01R
⇒2.5−1=0.01R
⇒1.5=0.01R
⇒R=1.50.01=150 ohms
The resistance to be added to the galvanometer to convert it into a voltmeter of range 2.5 volts is 150 ohms.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - B. Assertion and reason18videos
CURRENT ELECTRICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Match the columns4videos
CURRENT ELECTRICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Check point70videos
CURRENT ELECTRICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective11videos
COMMUNICATION SYSTEM
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery25videos
ELECTROMAGNETIC INDUCTION
Similar Questions
A galvanometer has a coil of resistance 100Ω and gives a full-scale deflection for 30mA current. If it is to work as a voltmeter of 30V range, the resistance required to be added will be
View SolutionA glavanometer of 50Ω resistance has 25 divisions. A current of 4×10−4 A gives a deflection of one division. To convert this galvanometer into a voltmeter having a range of 25V, it should be connected with a resistance of
View Solution
Knowledge Check
- Question 1 - Select One
A galvanometer of resistance 40Ω gives a deflection of 5 divisions per mA. There are 50 divisions on the scale. The maximum current that can pass through it when a shunt resistance of 2Ω is connected is
A210mAB155 MaC420mAD75 Ma
A galavanometer, whose resistance is 50 ohm has 25 divisions in it. When a current of 4×10−4 A passes through it,its needle (pointer) deflects by one division. To use this galvanometer as a volmeter of range 2.5V, it is should be connected to a resistance of :
View SolutionA galvanometer of resistance 10Ω shows full scale deflection for current 100 mA. The resistance that needs to be connected in series with the galvanometer so that it can be used to measure potential difference in the range 0-100 V is (in Ohm):
View SolutionA galvanometer of resistance 50Ω given full-scale deflection for a current of 10 mA is to be changed into a voltmeter of rang 100 V . What should be the Value of resistance to be added in series with this galvanometer ?
View SolutionA galvanometer of resistance 100Ω gives full deffection for a current 10−5 the value of shunt required to convert it into ammeter of range 1 ampere is:-
View SolutionA galvanometer of resistance 95Ω, shunted resistance of 5Ω, gives a deflection of 50 divisions when joined in series with a resistance of 20kΩ and a 2V accumulator. What is the current sensitivity of the galvanomter (in div/μA)?
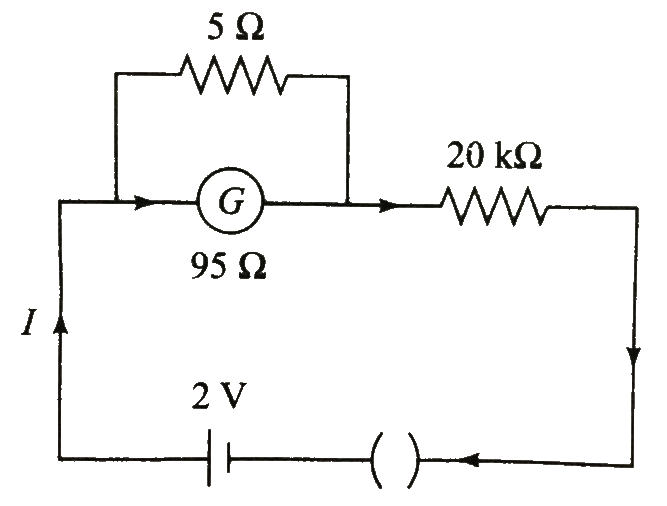 View Solution
View SolutionThe resistance of galvanometer is g ohm and the range is 1 volt. The value of resistance used to convert it into a voltmeter of ragne 10 volt is:-
View Solution100mA current gives a full scale deflection in a galvanometer of 2Ω resistance. The resistance connected with the galvanometer to convert it into a voltmeter to measure 5V is
View Solution

