Two electric bulbs rated 50 W and 100 V are glowing at full power, when used in parallel with a battery of emf 120 V and internal resistance 10 Ω. The maximum number of bulbs that can be connected in the circuit when glowing at full power, is
a) 6
b) 4
c) 2
d) 8
The correct Answer is:B
To solve the problem of determining the maximum number of bulbs that can be connected in parallel while glowing at full power, we will follow these steps:
Step 1: Calculate the resistance of each bulb
The resistance R of each bulb can be calculated using the formula:
R=V2P
where V is the voltage rating of the bulb and P is the power rating.
Given:
- Voltage rating V=100V
- Power rating P=50W
Substituting the values:
R=100250=1000050=200Ω
Step 2: Calculate the equivalent resistance of the two bulbs in parallel
When two resistors R1 and R2 are in parallel, the equivalent resistance Req can be calculated using the formula:
1Req=1R1+1R2
For two identical bulbs:
1Req=1200+1200=2200=1100
Thus,
Req=100Ω
Step 3: Calculate the total resistance in the circuit
The total resistance Rtotal in the circuit includes the internal resistance of the battery r=10Ω and the equivalent resistance of the bulbs:
Rtotal=Req+r=100+10=110Ω
Step 4: Calculate the power of the circuit
The power Pcircuit supplied by the battery can be calculated using the formula:
Pcircuit=V2Rtotal
where V is the EMF of the battery.
Given:
- EMF V=120V
Substituting the values:
Pcircuit=1202110=14400110≈130.91W
Step 5: Calculate the maximum number of bulbs
To find the maximum number of bulbs n that can glow at full power, we divide the total power of the circuit by the power of one bulb:
n=PcircuitPbulb=130.9150≈2.618
Since n must be a whole number, we take the integer part:
n=2
Conclusion
The maximum number of bulbs that can be connected in the circuit while glowing at full power is 2.
---
The resistance R of each bulb can be calculated using the formula:
R=V2P
where V is the voltage rating of the bulb and P is the power rating.
- Voltage rating V=100V
- Power rating P=50W
R=100250=1000050=200Ω
When two resistors R1 and R2 are in parallel, the equivalent resistance Req can be calculated using the formula:
1Req=1R1+1R2
For two identical bulbs:
1Req=1200+1200=2200=1100
Thus,
Req=100Ω
The total resistance Rtotal in the circuit includes the internal resistance of the battery r=10Ω and the equivalent resistance of the bulbs:
Rtotal=Req+r=100+10=110Ω
The power Pcircuit supplied by the battery can be calculated using the formula:
Pcircuit=V2Rtotal
where V is the EMF of the battery.
- EMF V=120V
Pcircuit=1202110=14400110≈130.91W
To find the maximum number of bulbs n that can glow at full power, we divide the total power of the circuit by the power of one bulb:
n=PcircuitPbulb=130.9150≈2.618
Since n must be a whole number, we take the integer part:
n=2
The maximum number of bulbs that can be connected in the circuit while glowing at full power is 2.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - B. Assertion and reason
18 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Match the columns
4 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Check point
70 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions
Electric bulb 50W−100V glowing at full power are to be used in parallel with battery 120V, 10Ω. Maximum number of bulbs that can be connected so that they glow in full power is
View SolutionThe emf of a battery is 2V and its internal resistance is 0.5Ω the maximum power which it can deliver to any external circuit will be
View SolutionWhen two electric bulbs of 40W and 60W are connected in parallel, then the:
View Solutiontwo heading coils of resistances 10Ωand20Ω are connected in parallel and connected to a battery of emf 12 V and internal resistance 1Ω Thele power consumed by the n are in the ratio
View SolutionTwo electric bulbs A and B are rated as 60 W and 100 W . They are connected in parallel to the same source. Then,
View SolutionThe figure shows two capacitors connected in parallel with two resistance and a battery of emf 10V , internal resistance 5Ω. At steady state.
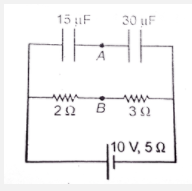
View SolutionAn electric bulb is rated 220Vand100W. When it is operated on 110V, the power consumed will be :
View SolutionAn electric bulb is rated "220 V, 100 W'.
What is its resistance ?
View SolutionAn electric bulb marked 25 W and 100 V is connected across 50 V supply . Now its power is .
View SolutionA bulb is connected to a battery of p.d. 4 V and internal resistance 2.5 Ω. A steady current of 0.5 A flows through the circuit. Calculate :
the resistance of the bulb,
View Solution
