
The variation of velocity of a particle executing SHM with time is shown is fig. The velocity of the particle when a phase change of π6 takes place from the instant it is at one of the extreme positions will be
A
3.53ms
B
2.5ms
C
4.330ms
D
none of these
Video Solution
Text Solution
The correct Answer is:B
From the graph T=(5−1)=4s
(distance between the two adjacent shown in the figure)
and vmax=5ms,ωA=5ms
(2πT)A=5⇒A=5T2π=5×42π=10π m
Also ω=2π4=π2rads
The equation of velocity can be written as
v=5sin((π2t))ms
At extreme position, v=0, sin((π2t))=0 or t=2s
Phase of the particle velocity at that insstant corresponding to the above equation =π
Therefore, when a phase change of π5 takes place, the resulting phase=π+π6
v=5sin((π+π6))=−5sin(π6)=−5(12)
=2.5ms (numerically)
dydt=v⇒dy=dt
dy=∫5sin((πt2))dt=10π[−co(sπt2)]+C
Since at t=0, the particle is at the extreme position, there fore at r=0,y=−10π
−10π=−10πcosθ+C⇒C=0
y=−10πcos(πt2)
Clearly a phase change of π6 corresponds to a time difference of T2π(π6)=T12=412=13s
y=−10πcos(π6)=−10π(√32)
=5√3πm (numerically)
Acceleration a=dvdt=ddt(5sin(πt)2)=5π2cosπt2
a at t=13s=5π2cos(π6)=5π√34ms2
Maximum displacement xmax=A=10πm
and maximum accceleration, amax=ω2A
=(π2)2×10π=5π2ms2
|
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct
35 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Assertion Reasoning
6 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Subjective
21 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
Knowledge Check
Average velocity of a particle executing SHM in one complete vibration is :
AzeroBAω2CAωDAω22Average velocity of a particle executing SHM in one complete vibration is :
AAω2BAωCAω22DZeroThe phase of a particle executing S.H.M is π/2 when it has
Amaximum displacementBmaximum velocityCmaximum energyDnone of the above
displacement versus time curve for a particle executing SHM is is as shown in figure.
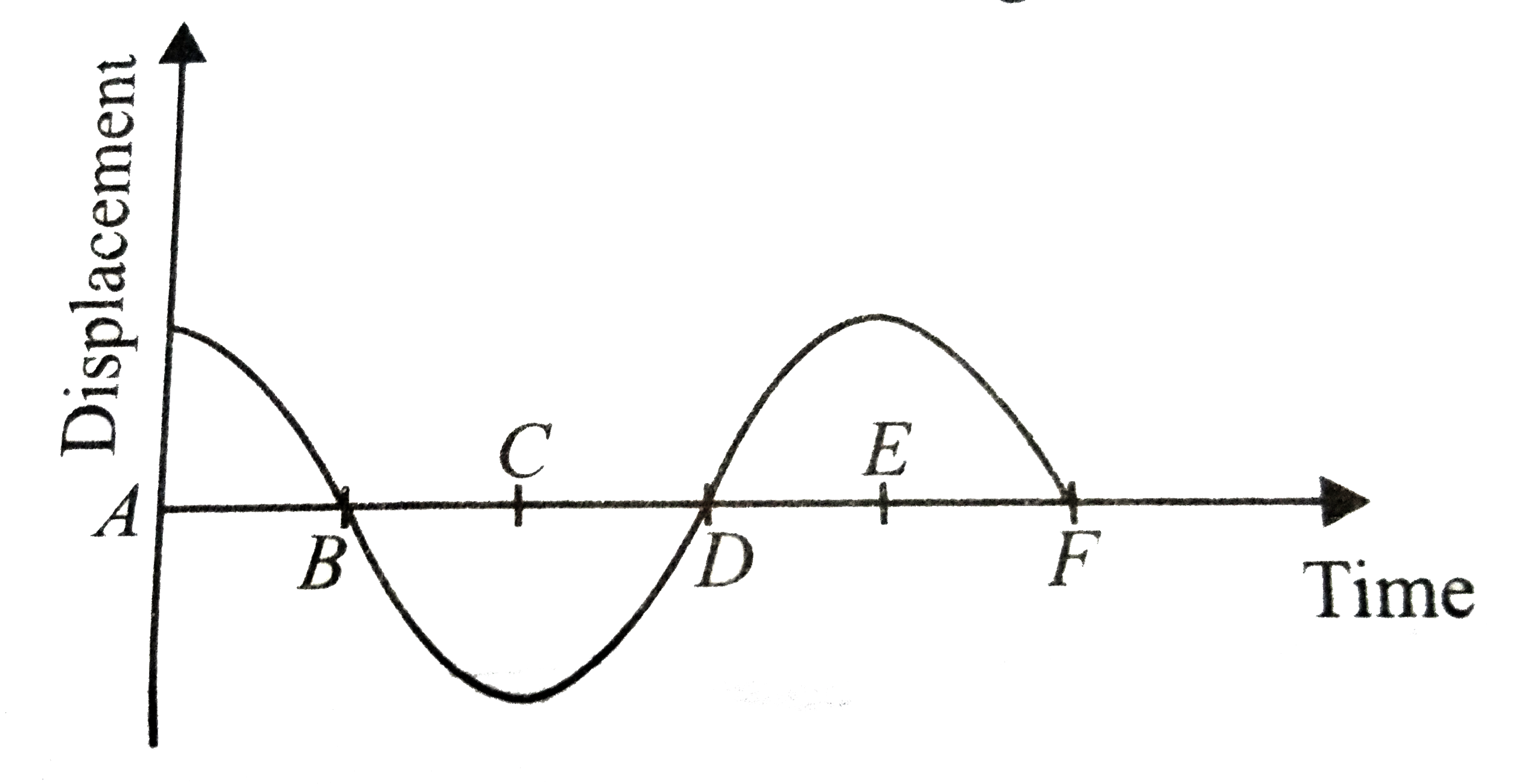
At what points the velocity of the particle is zero?
View SolutionThe velocity of a particle performing S.H.M. at extreme position is
View SolutionThe acceleration-displacement graph of a particle executing SHM is as shown in the figure. The velocity of the particle at y = 0 is (take tan14∘ = 0.25)
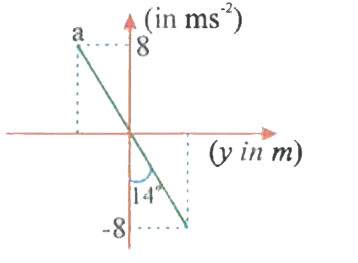
View SolutionVelocity-time graph of a particle executing SHM is shown in figure. Select the correct alternative(s).

View SolutionA particle executing SHM with time period T and amplitude A. The mean velocity of the particle averaged over quarter oscillation, is
View Solution

