The work done an a particle of mass m by a force
K⎡⎢
⎢⎣x(x2+y2)3/2ˆi+y(x2+y23/2)ˆj⎤⎥
⎥⎦
(K being a constant of appropriate dimensions), when the partical is taken from the point (a,0) to the point (0,a) along a circular path of radius a about the origin in x - y plane is
(a) 2Kxa
(b) Kxa
(c) Kx2a
(d) 0
The correct Answer is:D
To solve the problem of finding the work done on a particle of mass m by the given force as it moves along a circular path from the point (a,0) to the point (0,a), we can follow these steps:
Step 1: Identify the Force Acting on the Particle
The force acting on the particle is given by:
F=K(x(x2+y2)3/2^i+y(x2+y2)3/2^j)
Step 2: Define the Path of Motion
The particle moves along a circular path of radius a about the origin. The equation of the circular path is:
x2+y2=a2
As the particle moves from (a,0) to (0,a), it traces a quarter of the circle.
Step 3: Substitute the Circular Path into the Force Equation
Since x2+y2=a2, we can express the force in terms of a:
F=K(xa3^i+ya3^j)
This simplifies to:
F=Ka3(x^i+y^j)
Step 4: Analyze the Direction of Force and Displacement
The displacement ds of the particle along the circular path is always tangential to the circle. The force F is directed radially outward from the origin, while the displacement is tangential.
Step 5: Determine the Angle Between Force and Displacement
Since the force is radial and the displacement is tangential, the angle θ between the force and the displacement is 90∘.
Step 6: Calculate the Work Done
The work done W by a force is given by the dot product of the force and the displacement:
W=∫F⋅ds
However, since θ=90∘, we have:
cos(90∘)=0
Thus, the work done is:
W=|F||s|cos(90∘)=0
Conclusion
The work done on the particle as it moves from (a,0) to (0,a) along the circular path is:
0 joules
The force acting on the particle is given by:
F=K(x(x2+y2)3/2^i+y(x2+y2)3/2^j)
The particle moves along a circular path of radius a about the origin. The equation of the circular path is:
x2+y2=a2
As the particle moves from (a,0) to (0,a), it traces a quarter of the circle.
Since x2+y2=a2, we can express the force in terms of a:
F=K(xa3^i+ya3^j)
This simplifies to:
F=Ka3(x^i+y^j)
The displacement ds of the particle along the circular path is always tangential to the circle. The force F is directed radially outward from the origin, while the displacement is tangential.
Since the force is radial and the displacement is tangential, the angle θ between the force and the displacement is 90∘.
The work done W by a force is given by the dot product of the force and the displacement:
W=∫F⋅ds
However, since θ=90∘, we have:
cos(90∘)=0
Thus, the work done is:
W=|F||s|cos(90∘)=0
The work done on the particle as it moves from (a,0) to (0,a) along the circular path is:
0 joules
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Archives(multiple Correct)
3 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Archives (assertion-reasoning)
1 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Integer
14 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
Find the distance of the point (2,3) from the line 2x−3y+9=0 measured along a line x−y+1=0.
View SolutionDistance of point P on the curve y=x3/2 which is nearest to the point M (4, 0) from origin is
View SolutionThe maximum distance of the point (k,0) from the curve 2x2+y2−2x=0 is equal to
View SolutionIf the points (2, 1) and (1, −2) are equidistant from the point (x, y) , show that x+3y=0 .
View SolutionThe work done by the force F=A(y2ˆi+2x2ˆj), where A is a constant and x & y are in meters around the path shown in
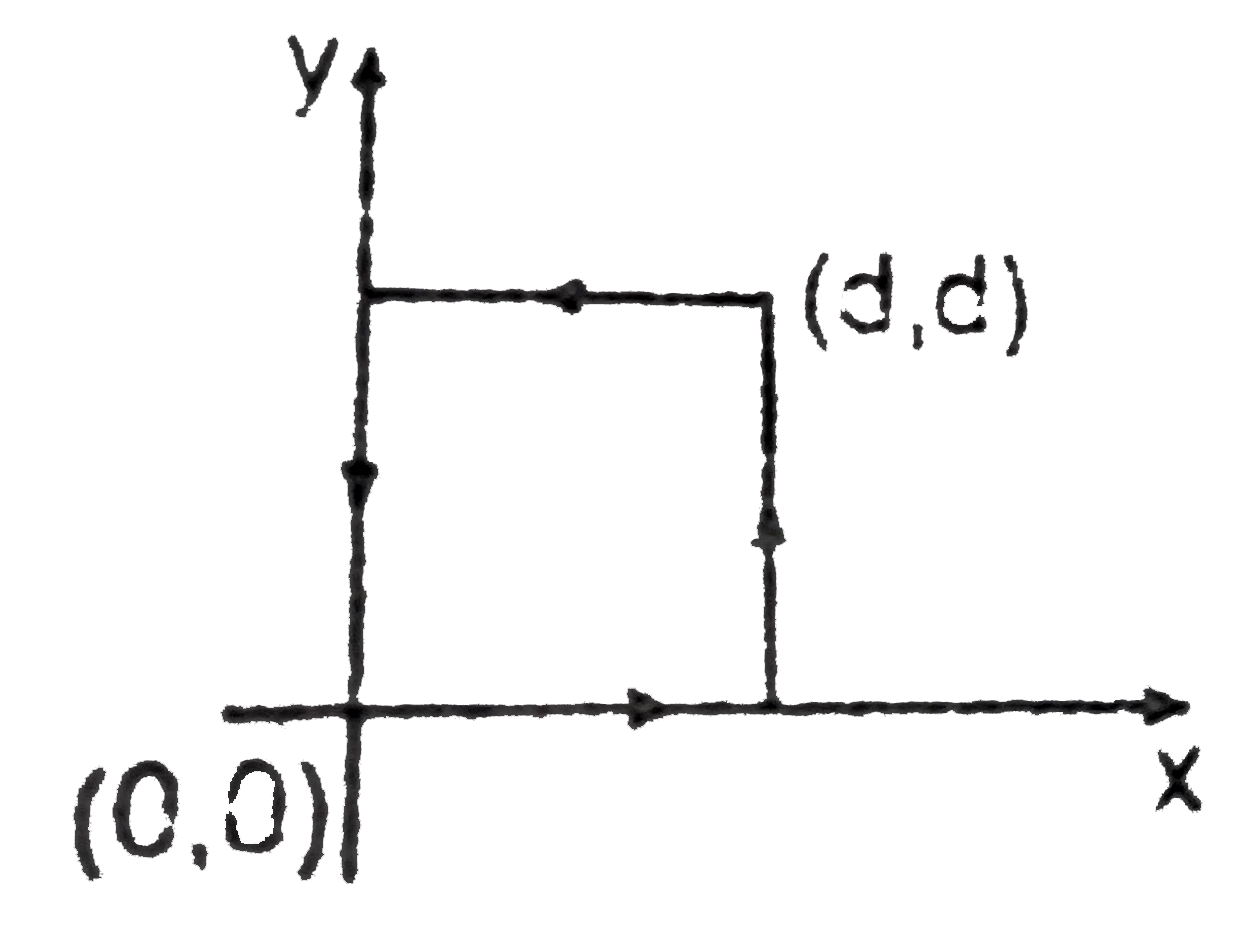
View SolutionA force F=−K(yˆi+xˆj) (where K is a positive constant) acts on a particle moving in the x-y plane. Starting from the origin, the particle is taken along the positive x-axis to the point (a,0), and then parallel to the y-axis to the point (a,a). The total work done by the force F on the particle is
View SolutionFind what the following equation become when the origin is shifted to the point (1,1): x2+xy−3x−y+2=0
View SolutionA particle of mass m and charge q is in a electric and magnetic field given by
→E=2ˆi+3ˆj,→B=4ˆj+6ˆk
The charged particle is shifted form the origin to the point P(x = 1, y=1) along a striaght path. The magnitude of the total work done is :
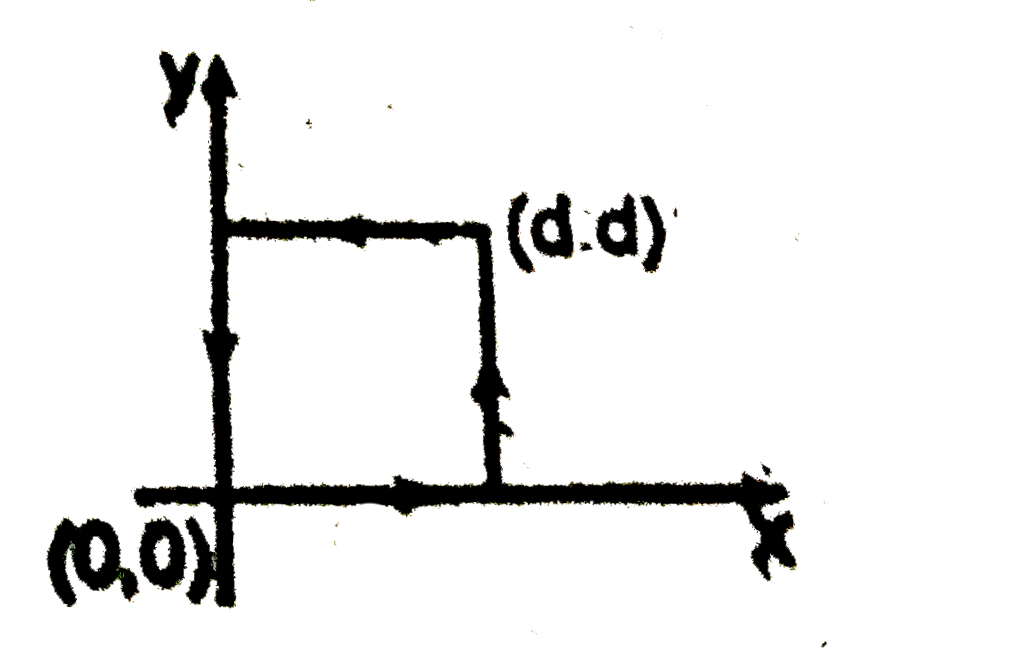
View SolutionThe work done by the force →F=A(y2ˆi+2x2ˆj), where A is a constant and x & y are in meters around the path shown is :
View SolutionThe distance of the point (1,−2,4) from the plane passing through the point (1,2,2) perpendicular to the planes x−y+2z=3 and 2x−2y+z+12=0 is
View Solution
