There are two oscillating circuits (figure) with capacitors of equal capacitances. How must inductances and active resistances of the coils be interrelated for the frequencies and damping of free oscillations in both circuits to be equal ? The mutual inductance of coils in the left circuit is negligible.

We have
L1.I1+R1I1=L2.I2+R2I2
=−∫IdtC
I=I1+I2
Then differentiating we have the equations
L1C..I1+R1C.I1+(I1+I2)=0
L2C..I2+R2C.I2+(I1+I2)=0
Look for a solution
I1=A1eαt,I2=A2eαt
Then (1+α2L1C+αR1C)A1+A2=0
A1=(1+α2L2C+αR2C)2=0
This set of simultaneous equation has a nontrivial solution only if
(a+α2L1C+αR1C.)(1+α2L2C+αR2C)=1
or α3+α2L1R2+L2R1L1L2+αL1+L2+R1R2CL1L2C+R1+R2L1L2C=0
This cubic equation has one real root which we ignore and two complex conjugate roots. We require the condition that this pair of complex conjugate roots is identical with roots of the equation
α2LC=αRC+1=0
The general solution of this problem is not easy . We look for special cases. If R1=R2=0, then R=0, and L=L1L2L1+L2. If L1=L2=0,then
L=0 and R=R1R2/(R1+R2). These are the quoted solution but they are misleading. We shall give the solution for small R1,R2. Then we put α=−β+iω when β is small
We get (1- omega^(2)L_(1)C-2ibetaomegaL_(1)C-betacancel(R_(1))C+iomegaR_(1)C)
(1- omega^(2)L_(2)C-2ibetaomegaL_(2)C-betacancel(R_(2))C+iomegaR_(2)C)=1
( we neglect β2&βR1,βR2). Then (1−ω2L1C)(1−ω2L2C)=1⇒ω2=L1+L2L1L1C
This is identical with ω2=1LC if L=L1L2L1+L2. also(2βL1−R2)(1−ω2L2C)+(2βL2−R2)(1−ω2L2C)=0
This gives β=R2L=R1L22+R2L212L1L2(L1+L2)⇒R=R1L22+R2L21(L1+L2)2

Topper's Solved these Questions
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Elastic Waves
39 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Exercise
2 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics
49 Videos
Similar Questions
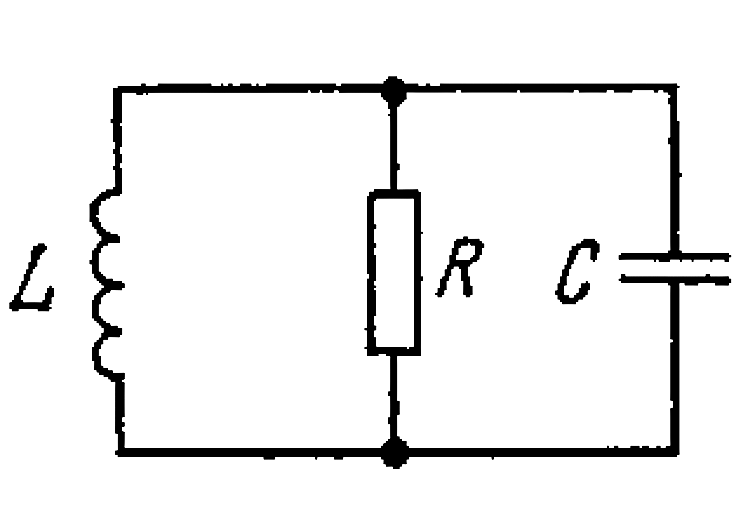
Find the damped oscillation frequency of the circuit shown in figure. The capacitance C, inductance L, and active resistance R are supposed to be known. Find how must C,L,andR be interrelated to make oscillations possible.
View SolutionA transmitter operates at 1 MHz. The oscillating circuit has a capacitance of 200 pF. What is the inductance and capacitative reactance of the resonant circuit ?
View Solution
Knowledge Check
If for above circuit the capacitive reactance is two times of inductive Reactance, and resistance R is equal to inductance Reactance then power factor of circuit is .
 A1BzeroC12D2√5
A1BzeroC12D2√5In figure when key is pressed the ammeter A reads i ampere . The charge passing in the galvanometer circuit of total resistance R is Q . The mutual inductance of the two coils is
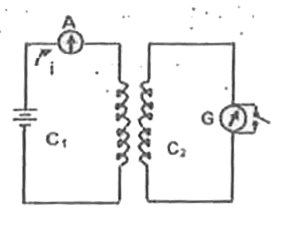 AQ/RBQ/RCQR/iDi/QR
AQ/RBQ/RCQR/iDi/QR
An oscillating circuuit incorporates a leaking capacitor. Its capacitance is equal C and active resistance to R. The coil inductance is is L. The resistance of the coil and the wires is negligible. Find :
(a) the damped oscillation frequecy of such a circuit ,
(b) its quality factor.
View SolutionA certain oscillating circuit consits of a capacitor with capacitance C, a coil with inductance L and active resistance R, and a switch . When the swith was disconnected, the capacitor was charged, then the switch was closed and oscillations set in. Find the ratio of the voltage across the capacitor to its peak value at the moment immediatel after closing the switch.
View SolutionAn oscillating circuit consists of a capacitor with capacitance C=1.2nF and a coil with inductance L=6.0μH and active resistance R=0.50Ω. What mean power should be fed to the circuit to maintain undamped harmonic oscillations with volage amplitude acroos the capacitor being equal to Vm=10V?
View SolutionIf for above circuit the capacitive reactance is two times of inductive Reactance, and resistance R is equal to inductance Reactance then power factor of circuit is .

View SolutionAn oscillating circuit consist of a capacitor with capacitance C=4.0μF and a coil with inductance L=2.0μH and active resistance R=10Ω. Find the ration of the energy of the coil's magnetic field to that of the capacitor's electric field at the moment when the current has the maximum value .
View SolutionA circuit consists of a capacitor with capacitance C and a coil with active resistance R and inductance L connected in parallel. Find the impedane of the circuit at frequency ω of alternating voltage.
View Solution
