Three capacitors having capanctances 20μF,30μF and 40μF are conneceted in series with a 12V battary. Find the charge on each of the capacitors. How much work has been done by the battery in charging the capacitors?
To solve the problem step by step, we will follow these instructions:
Step 1: Determine the Equivalent Capacitance
For capacitors connected in series, the formula for the equivalent capacitance C is given by:
1C=1C1+1C2+1C3
Where:
- C1=20μF
- C2=30μF
- C3=40μF
Substituting the values:
1C=120+130+140
Step 2: Find a Common Denominator
To add the fractions, we find a common denominator. The least common multiple (LCM) of 20, 30, and 40 is 120.
1C=6120+4120+3120=13120
Step 3: Calculate the Equivalent Capacitance
Now, we can find C:
C=12013≈9.23μF
Step 4: Calculate the Charge on Each Capacitor
The charge Q on the capacitors in series is given by:
Q=C⋅V
Where V=12V. Substituting the values:
Q=9.23×10−6F×12V≈110.76μC
Step 5: Calculate the Work Done by the Battery
The work done W by the battery in charging the capacitors is given by:
W=Q⋅V
Substituting the values:
W=110.76×10−6C×12V≈1.33×10−3J
Final Answers
- The charge on each capacitor is approximately 110.76μC.
- The work done by the battery is approximately 1.33×10−3J.
---
For capacitors connected in series, the formula for the equivalent capacitance C is given by:
- C1=20μF
- C2=30μF
- C3=40μF
To add the fractions, we find a common denominator. The least common multiple (LCM) of 20, 30, and 40 is 120.
Now, we can find C:
The charge Q on the capacitors in series is given by:
The work done W by the battery in charging the capacitors is given by:
- The charge on each capacitor is approximately 110.76μC.
- The work done by the battery is approximately 1.33×10−3J.
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - CAPACITORSEXERCISE - short answer7videos
CAPACITORS
- BOOK - HC VERMA ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE 26videos
CAPACITORS
- BOOK - HC VERMA ENGLISHCHAPTER - BOHR'S MODEL AND PHYSICS OF THE ATOMEXERCISE - Short Answer10videos
BOHR'S MODEL AND PHYSICS OF THE ATOM
- BOOK - HC VERMA ENGLISHCHAPTER - DISPERSION AND SPECTRAEXERCISE - Question for short Answer6videos
DISPERSION AND SPECTRA
Similar Questions
Find the charges on 6μF and 4μF capacitors
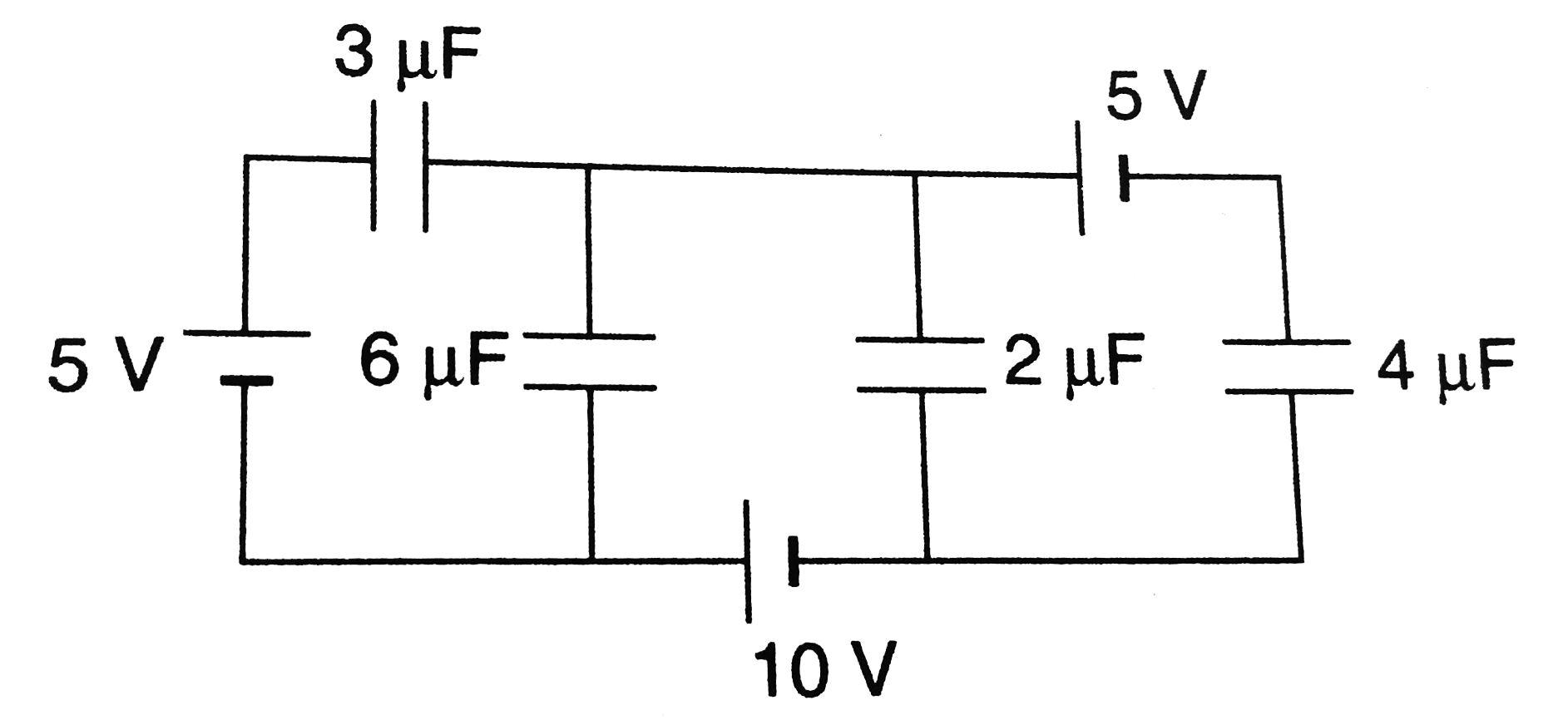 View Solution
View SolutionTwo capacitors of 10μF and 20μF are connected in series with a 30V battery. The charge on the capacitors will be, respectively
View SolutionTwo capacitor of capacitance 4.0μFand 6.0muF' are connected in series with a battery of 20 V . Find the energy supplied by the battery .
View SolutionTwo capacitors of capacitance of 6μFand12μF are connected in series with a battery. The voltage across the 6μF capacitor is 2V. Compute the total battery voltage.
View SolutionThree capacitors of capacitances 2μF, 3μF and 6μF are connected in series with a 12 V battery. All the connecting wire are disconnected, the three positive plates are connected together and the three negative plates are connected together. Find the charges on the three capacitors after the reconnection.
View SolutionThree capacitors having capacitances of 8.4μF,8.4μF and 4.2μF are connected in series across a 36 potential difference.
(a) What is the charge on 4.2μF capacitor?
(b) What is the total energy stored in all three capacitors?
(c) The capacitors are disconnected from the potential difference without allowing them to discharge. They are then reconnected in parallel with each other, with the positively charged plates connected together. What is the voltage across each capacitor in the parallel combination?
(d) What is the total energy now stored in the capacitors?View SolutionThree capacitors 3μF,6μF and 6μF are connected in series to source of 120 V. The potential difference in volt, across the 3μF capacitor will be
View SolutionIn steady state, find the charge on 3μF capacitor in μC
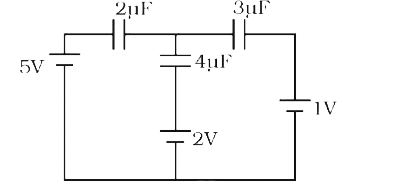 View Solution
View SolutionThree capacitors of capacitances 3μF, 6μF, and 4μF are connected as shown across a battery of emf 6V.
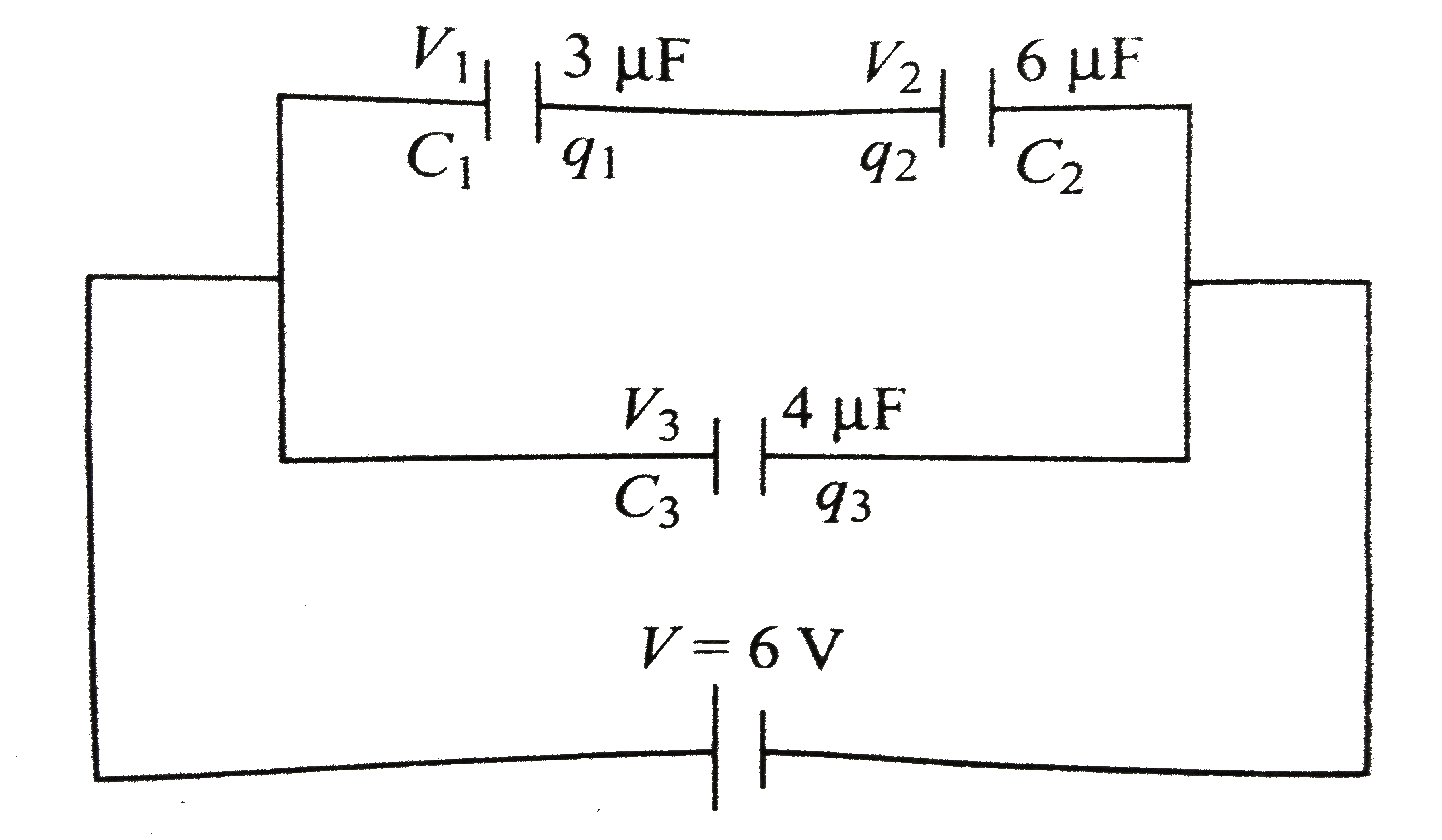 .
.
i. Find the equivalent capacitance,
ii. Find the potential difference and charge on each capacitor.
iii. Find the energy stored in the system of capacitors and total energy stored in the system of capacitor.View SolutionThree capcitors of capacitances 4μF,
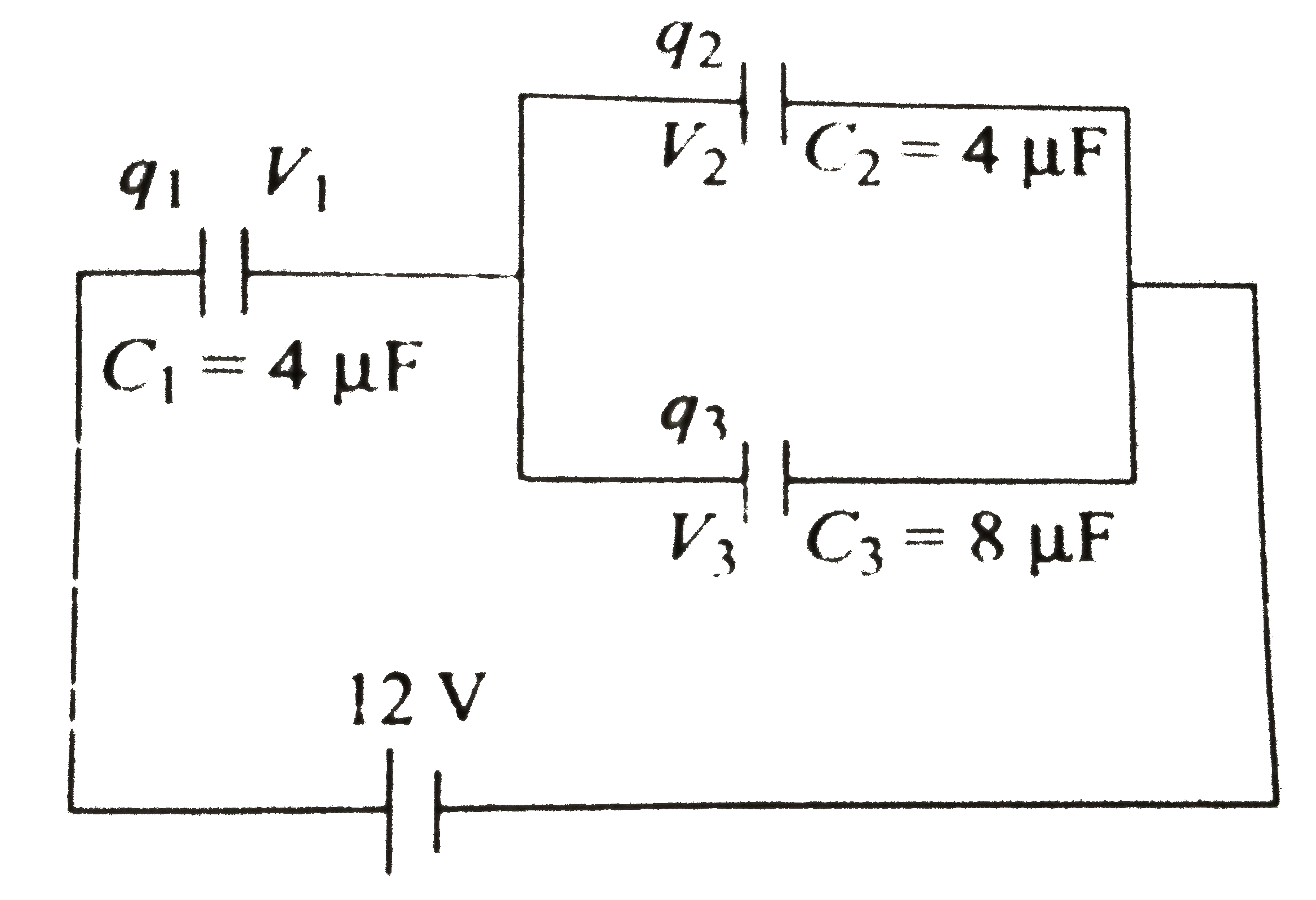 .
.
4μF, and 8μF, are connected as show across a battery of emf 12V.
i. Find the equivalent capacitane.
ii. Find the potential difference and charge on each capacitor.
iii. Find the energy stored in each capacitor and the total energy stored in the system of capacitors.View Solution
