Three children are sitting on a see-saw in such a way that is balances. A 20kg and a 30kg boy are on opposite sides at a distance of 2m from the pivot. It the third boy jumps off, thereby destroying balance, then the initial angular acceleration of the board is: (Neglect weight of board)
A. 0.01rads−2
B. 1.0rads−2
C. 10rads−2
D. 100rads−2
The correct Answer is:B
To solve the problem step by step, we will follow these steps:
Step 1: Understand the Initial Conditions
We have two boys on a seesaw, one weighing 20 kg (m1) and the other weighing 30 kg (m2). They are positioned 2 meters away from the pivot on opposite sides, and the seesaw is balanced initially.
Step 2: Identify the Forces and Torques
When the third boy jumps off, the seesaw will no longer be balanced. The forces acting on the seesaw due to the weights of the two boys will create torques about the pivot.
- The torque due to m1 (20 kg) is given by:
τ1=m1⋅g⋅r1=20⋅g⋅2
- The torque due to m2 (30 kg) is given by:
τ2=m2⋅g⋅r2=30⋅g⋅2
Step 3: Calculate the Net Torque
The net torque (τ_net) acting on the seesaw is the difference between the torques due to m2 and m1:
τnet=τ2−τ1=(30⋅g⋅2)−(20⋅g⋅2)
Substituting g=10m/s2:
τnet=(30⋅10⋅2)−(20⋅10⋅2)=600−400=200N m
Step 4: Calculate the Moment of Inertia
The moment of inertia (I) of the system can be calculated using the formula:
I=m1⋅r21+m2⋅r22
Substituting the values:
I=(20⋅22)+(30⋅22)=(20⋅4)+(30⋅4)=80+120=200kg m2
Step 5: Calculate Angular Acceleration
Using the relationship between torque and angular acceleration:
τnet=I⋅α
We can rearrange this to find the angular acceleration (α):
α=τnetI=200200=1rad/s2
Final Answer
The initial angular acceleration of the seesaw after the third boy jumps off is:
α=1rad/s2
---
We have two boys on a seesaw, one weighing 20 kg (m1) and the other weighing 30 kg (m2). They are positioned 2 meters away from the pivot on opposite sides, and the seesaw is balanced initially.
When the third boy jumps off, the seesaw will no longer be balanced. The forces acting on the seesaw due to the weights of the two boys will create torques about the pivot.
τ1=m1⋅g⋅r1=20⋅g⋅2
- The torque due to m2 (30 kg) is given by:
τ2=m2⋅g⋅r2=30⋅g⋅2
The net torque (τ_net) acting on the seesaw is the difference between the torques due to m2 and m1:
τnet=τ2−τ1=(30⋅g⋅2)−(20⋅g⋅2)
τnet=(30⋅10⋅2)−(20⋅10⋅2)=600−400=200N m
The moment of inertia (I) of the system can be calculated using the formula:
I=m1⋅r21+m2⋅r22
Substituting the values:
I=(20⋅22)+(30⋅22)=(20⋅4)+(30⋅4)=80+120=200kg m2
Using the relationship between torque and angular acceleration:
τnet=I⋅α
We can rearrange this to find the angular acceleration (α):
α=τnetI=200200=1rad/s2
The initial angular acceleration of the seesaw after the third boy jumps off is:
α=1rad/s2
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Multiple Correct
9 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Linked Comprehension
28 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Subjective
13 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
Similar Questions
A boy of mass 30 kg is sitting at a distance of 2 m from the middle of a see-saw. Where should a boy of mass 40 kg sit so as to balance the see-saw ?
View SolutionOn a see saw, two chlidren of masses of 30kg and 50kg are sitting on one side of at distances 2m and 2.5m respectively from its middle. Where should a man of mass 74 kg sit to balance it?
View Solution
Knowledge Check
Karan of mass 45kg and Geeta of mass 30kg are sitting on a see saw at a distance of 2m and 1.5m respectively from the centre of the see saw in an amusement park as shown in the figure. Is the see saw in rotational equilibrium?
 AYesBNoCdata incompleteDNone of the above
AYesBNoCdata incompleteDNone of the above
A uniform seesaw, 5m long, is supported at its centre. A boy weighing 40 kgf sits at a distance of 1 m from the centre of the seesaw.
(i) To which class of lever does it belong ?
(ii) Find where a girl of weight 20 kgf must sit on the seesaw so as the balance the weight of the boy.
View SolutionA light rod of length 1 m is pivoted at its centre and two masses of 5 kg and 2 kg are hung from the ends as shown in the figure. Find the initial angular acceleration of the rod assuming that it was horizontal in the beginning.

View SolutionTwo 20kg cannon balls are chained together and fired horizontally with a velocity of 200m/s from the top of a 30m wall. The chain breaks during the flight of the cannon balls and one of them strikes the ground at t=2s, at a distance of 250m from the foot fo the wall, and 5m to the right of line of fire determine the position of the other cannon ball at that instant Neglect the resistance of air.

View SolutionA boy (30 kg) sitting on his horse whips it. The horse speeds up at an average acceleration of 2.0ms2. A. If the boy does not slide back, what is the force of friction exerted by the horse on the boy? b.If the boy slides back during the acceleration, what can be said about the coefficient of static friction between the horse and the boy. Take g=10ms2
View SolutionSpring is mounted as shown in figure. By attaching a mass to the free end and pulling side ways, we determine that the force is proportional to the displacement a force of 4N causing a displacement of 0.02 m. We attach a 2kg body to the end, pull it aside through a distance of 0.04m , and then released. Find
the velocity adn acceleration when the body has moved half way in toward the central from is initial position.
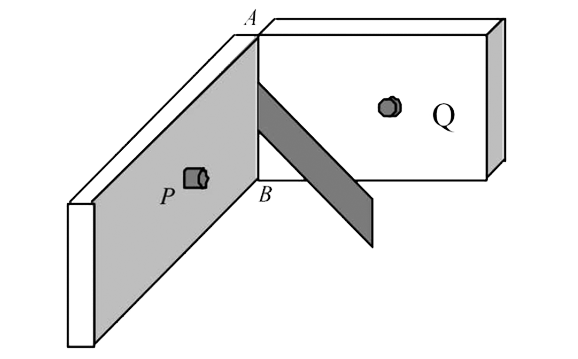
View SolutionTwo heavy metallic plates are joined together at 90∘ to each other. A laminar sheet of mass 30kg is hinged at the line AB joining the two heavy metallic plates. The hinges are frictionless. The moment of inertia of the laminar sheet about an axis parallel to AB and passing through its center of mass is 1.2 kg m2. Two rubber obstacles P and Q are fixed, one on each metallic plate at a distance 0.5m from the line AB. This distance is chosen so that the reaction due to the hinges on the laminar sheet is zero during the impact. Initially the laminar sheet hits one of the obstacles with an angular velocity 1 rad/s and turns back. If the impulse on the sheet due to each obstacal is 6 N-s,
(a) Find the location of the center of mass of the laminar sheet from AB.
(b) At what angular velocity does the laminar sheet come back after the first impact?
(c) After how many impacts, does the laminar sheet come to rest?
View SolutionTwo painters are working from a wooden hoard 5m long suspended from the top of a building by two ropes attached to the ends of the plank. Either rope can withstand a maximum tension of 1040N. Painter A of mass 80kg is working at a distance of 1m from one end. Painter B of mass 60kg is working at a distance of x in from the centre of mass of the board on the other side. Take mass of the board as 20kg and g=10ms−2. The range of x so that both the painters can work safely is
View Solution