Three equal charges are placed on the three corners of a square. If the force between q1 and q2 is F12 and that between q1 and q3 is F13, then the ratio of magnitudes (F12/F13) is
1/2
2
1/√2
√2
The correct Answer is:B
To solve the problem, we will analyze the forces acting between the charges at the corners of the square.
Step 1: Understand the Configuration
We have three equal charges q1, q2, and q3 placed at three corners of a square. Let's denote the side length of the square as a.
Step 2: Calculate the Force F12
The force between q1 and q2 (which are at adjacent corners) can be calculated using Coulomb's Law:
F12=kq1q2r2
Here, r is the distance between q1 and q2, which is equal to a (the side of the square). Since the charges are equal, we can denote them as q:
F12=kq2a2
Step 3: Calculate the Force F13
The force between q1 and q3 (which are at opposite corners of the square) is also calculated using Coulomb's Law. The distance between q1 and q3 is the diagonal of the square, which can be calculated using the Pythagorean theorem:
r=√a2+a2=a√2
Thus, the force F13 is given by:
F13=kq1q3(a√2)2=kq22a2
Step 4: Find the Ratio F12F13
Now we can find the ratio of the magnitudes of the forces:
F12F13=kq2a2kq22a2=112=2
Conclusion
The ratio of the magnitudes of the forces F12 and F13 is:
F12F13=2
Final Answer
Thus, the answer is 2.
---
We have three equal charges q1, q2, and q3 placed at three corners of a square. Let's denote the side length of the square as a.
The force between q1 and q2 (which are at adjacent corners) can be calculated using Coulomb's Law:
The force between q1 and q3 (which are at opposite corners of the square) is also calculated using Coulomb's Law. The distance between q1 and q3 is the diagonal of the square, which can be calculated using the Pythagorean theorem:
Now we can find the ratio of the magnitudes of the forces:
The ratio of the magnitudes of the forces F12 and F13 is:
Thus, the answer is 2.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Assertion and Reason
15 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Match the columns
5 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Check point 1.5
20 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions
135 Videos
Similar Questions
Three charges, each equal to q, are placed at the three. corners of a square of side a . Find the electric field at. the fourth corner.
View SolutionThree charges, each equal to q, are placed at the three. corners of a square of side a . Find the electric field at. the fourth corner.
View SolutionEqual charges Q are placed at the four corners A, B, C, D of a square of length a. The magnitude of the force on the charge at B will be
View SolutionLooking at the vanous electric lines of forces between charges Q1 and Q2 find the value of Q1Q2
View SolutionThree charges −q1,+q2 and −q3 are placed as shown in the figure. The x-component of the force on −q1 is proportional to
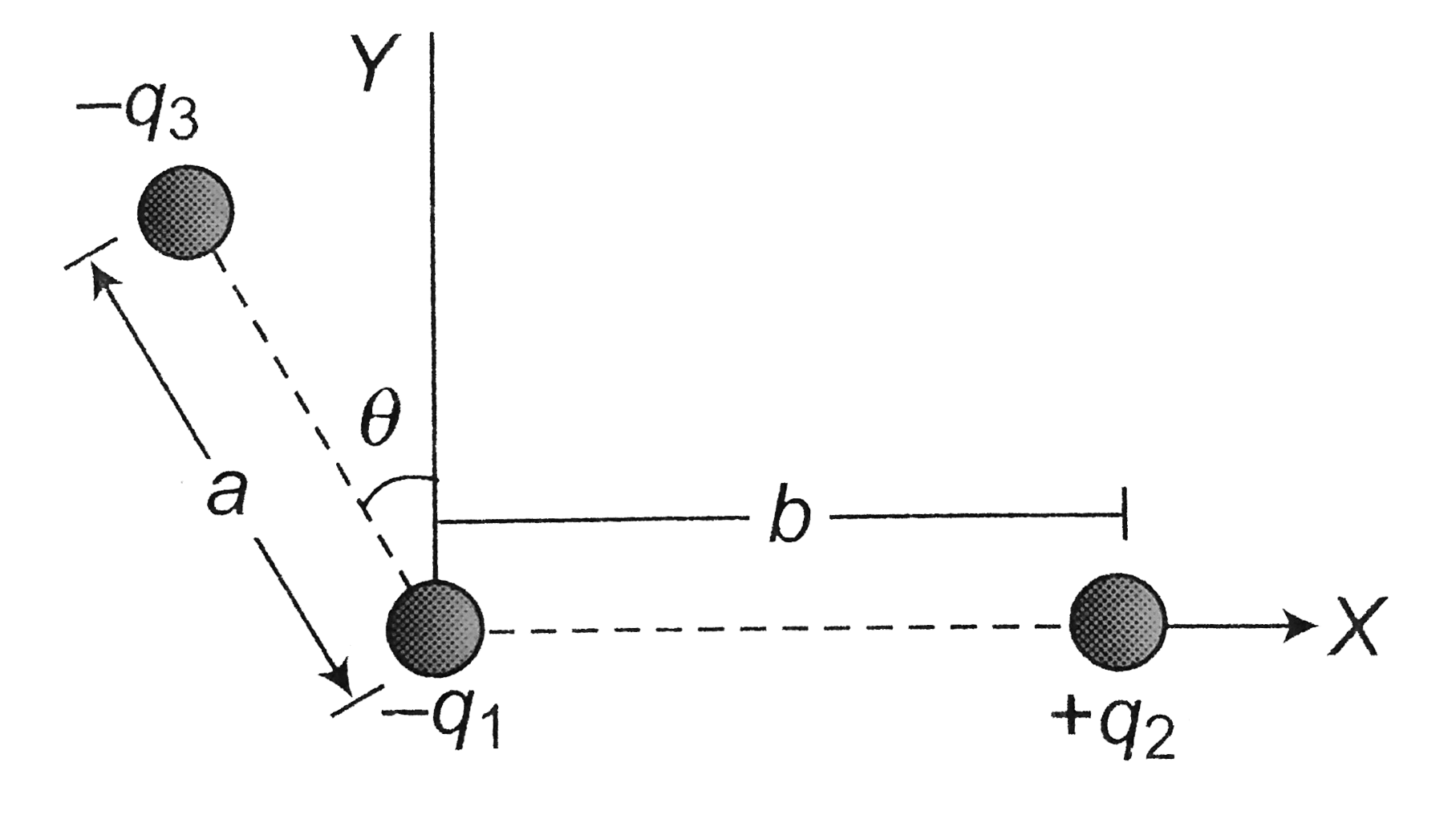
View SolutionFour point charges −Q,−q,2q and 2Q are placed, one at each corner of the square. The relation between Q and q for which the potential at the centre of the square is zero is
View SolutionFour point charges −Q,−q,2q and 2Q are placed, one at each corner of the square. The relation between Q and q for which the potential at the centre of the square is zero is
View SolutionFour charge Q,q,Q and q are kept at the four corners of a square as shown below. What is the relation between Q and q, so that the net force on a charge q is zero ?

View SolutionLooking at the various electric lines of forces between charges Q1 and Q2 , find the value of Q1Q2

View SolutionFour charges of +q, +q +q and +q are placed at the corners A, B, C and D of s square. The resultant force on the charge at D
View Solution
