Three identical metallic uncharged spheres A, B and C of radius a are kept on the corners of an equilateral triangle of side d(d>>a). A fourth sphere (radius a) which has charge Q touches A and is then removed to a position for away. B is earthed and then the earth connection is removed. c is then earthed. The charge on C is
Qa2d(2d−a2d)
Qa2d(2d−ad)
Qa2d(a−dd)
2Qad(d−a2d)
The correct Answer is:C
To solve the problem step by step, we will analyze the situation involving the metallic spheres and the charges they acquire through touching and earthing.
Step 1: Initial Setup
We have three identical metallic uncharged spheres A, B, and C at the corners of an equilateral triangle with side length d (where d≫a). A fourth sphere (let's call it D) with charge Q touches sphere A.
Step 2: Charge Distribution After Touching
When sphere D (with charge Q) touches sphere A, charge will redistribute between them because they are identical spheres. The total charge Q will be equally divided between A and D.
- Charge on A after touching: QA=Q2
- Charge on D after touching: QD=Q2
Step 3: Earthing Sphere B
Next, sphere B is earthed. When a sphere is earthed, its potential becomes zero. The potential VB of sphere B due to its own charge and the influence of sphere A can be expressed as:
VB=kQAd+kQBd=0
Where k is Coulomb's constant, and QB is the charge on sphere B after earthing. Since sphere B is initially uncharged, we can set QB to be the charge that B acquires after earthing.
Substituting QA=Q2:
kQ2d+kQBd=0
Step 4: Solving for Charge on Sphere B
Rearranging the equation gives:
QBd=−Q2d
Thus,
QB=−Q2
Step 5: Removing the Earth Connection from Sphere B
After earthing, when the connection is removed, sphere B retains the charge:
QB=−Q2
Step 6: Earthing Sphere C
Now, we earth sphere C. The potential of sphere C can be expressed as:
VC=kQAd+kQBd+kQCa=0
Where QC is the charge on sphere C after earthing.
Substituting the known charges:
kQ/2d+k(−Q2)1d+kQCa=0
Step 7: Simplifying the Equation
This simplifies to:
k(Q/2−Q/2d+QCa)=0
Thus, we have:
QCa=0
This implies:
QC=0
Conclusion
The charge on sphere C after the entire process is QC=0.
We have three identical metallic uncharged spheres A, B, and C at the corners of an equilateral triangle with side length d (where d≫a). A fourth sphere (let's call it D) with charge Q touches sphere A.
When sphere D (with charge Q) touches sphere A, charge will redistribute between them because they are identical spheres. The total charge Q will be equally divided between A and D.
- Charge on D after touching: QD=Q2
Next, sphere B is earthed. When a sphere is earthed, its potential becomes zero. The potential VB of sphere B due to its own charge and the influence of sphere A can be expressed as:
Rearranging the equation gives:
After earthing, when the connection is removed, sphere B retains the charge:
Now, we earth sphere C. The potential of sphere C can be expressed as:
This simplifies to:
The charge on sphere C after the entire process is QC=0.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (B) Chapter exercises
17 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.5
20 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
Three identical metallic uncheged spheres A,B,andC, each of radius a, are kept at the corners of an equilateral triangle of side d(d>>a) as shown in (Fig. 3.137). The fourth sphere (of radius a), which has a charge q, touches A and is then removed a position far away. B is earthed and then the earth connection is removed. C is then earthed. The charge on C is
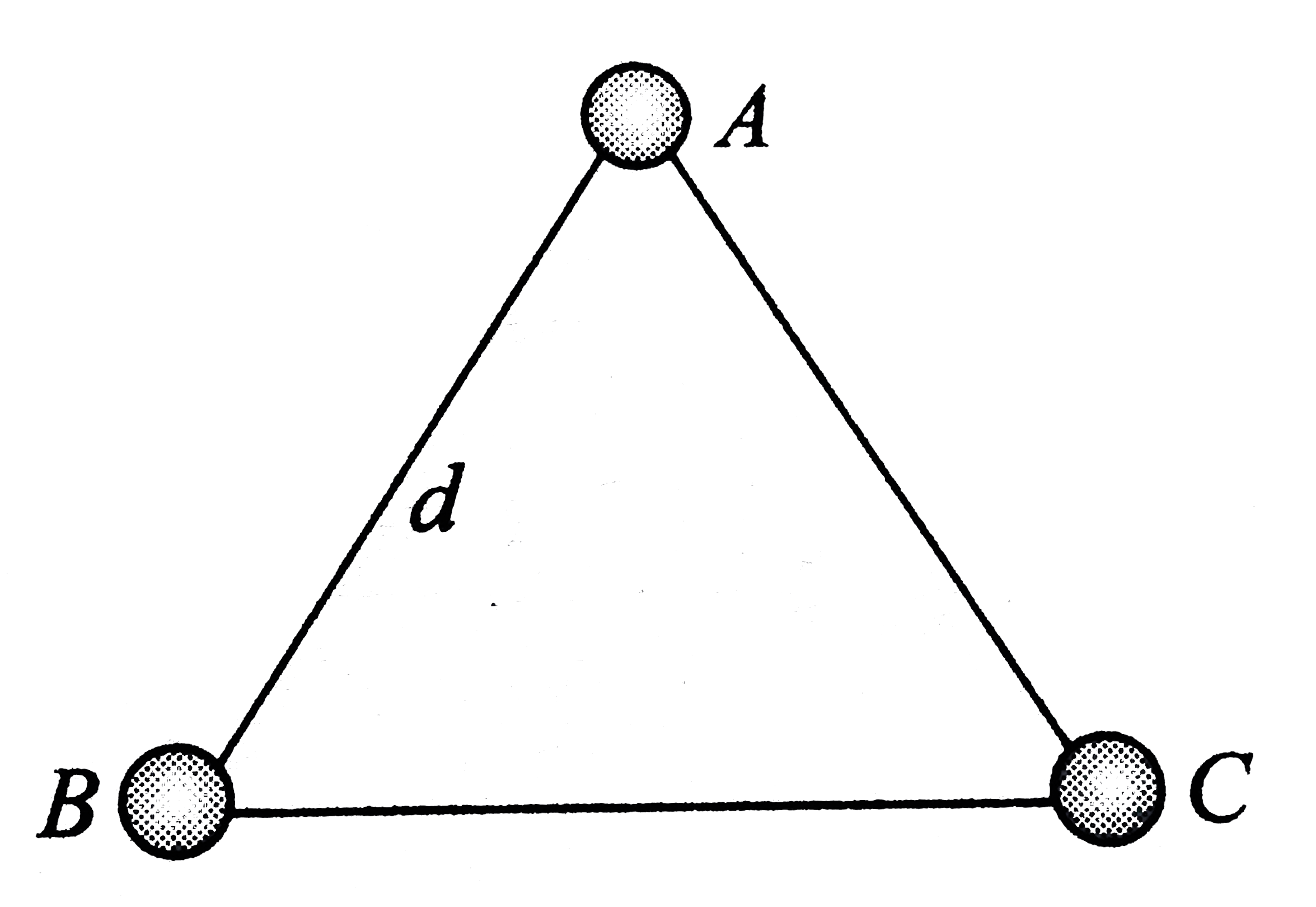 .
.
View SolutionThree charges +q, -q and +q are kept at the corners of an equilateral triangle of side d. Find the resultant electric force on a charge +q placed at the centroid O of the triangle.
View SolutionThree identical charges, each having a value 1.0×10−8C, are placed at the corners of an equilateral triangle of side 20 cm find the electric field and potential at the centre of the triangle.
View SolutionThere are two uncharged identicasl metallic spheres 1 and 2 of radius r separated by a distance d(d>>r). A charged metalllic sphere of same radius having charge q is touched with one of the sphere. After some time it is moved away fom the system. Now, the uncharged sphere is earthed. Charge on earthed sphere is
View SolutionThree identical dipoles with charges q and −q, and separation A between the charges, are placed at the corners of an equilateral triangle of side D as shown in (Fig. 3.123). Find the interaction energy of the system (a<<d).
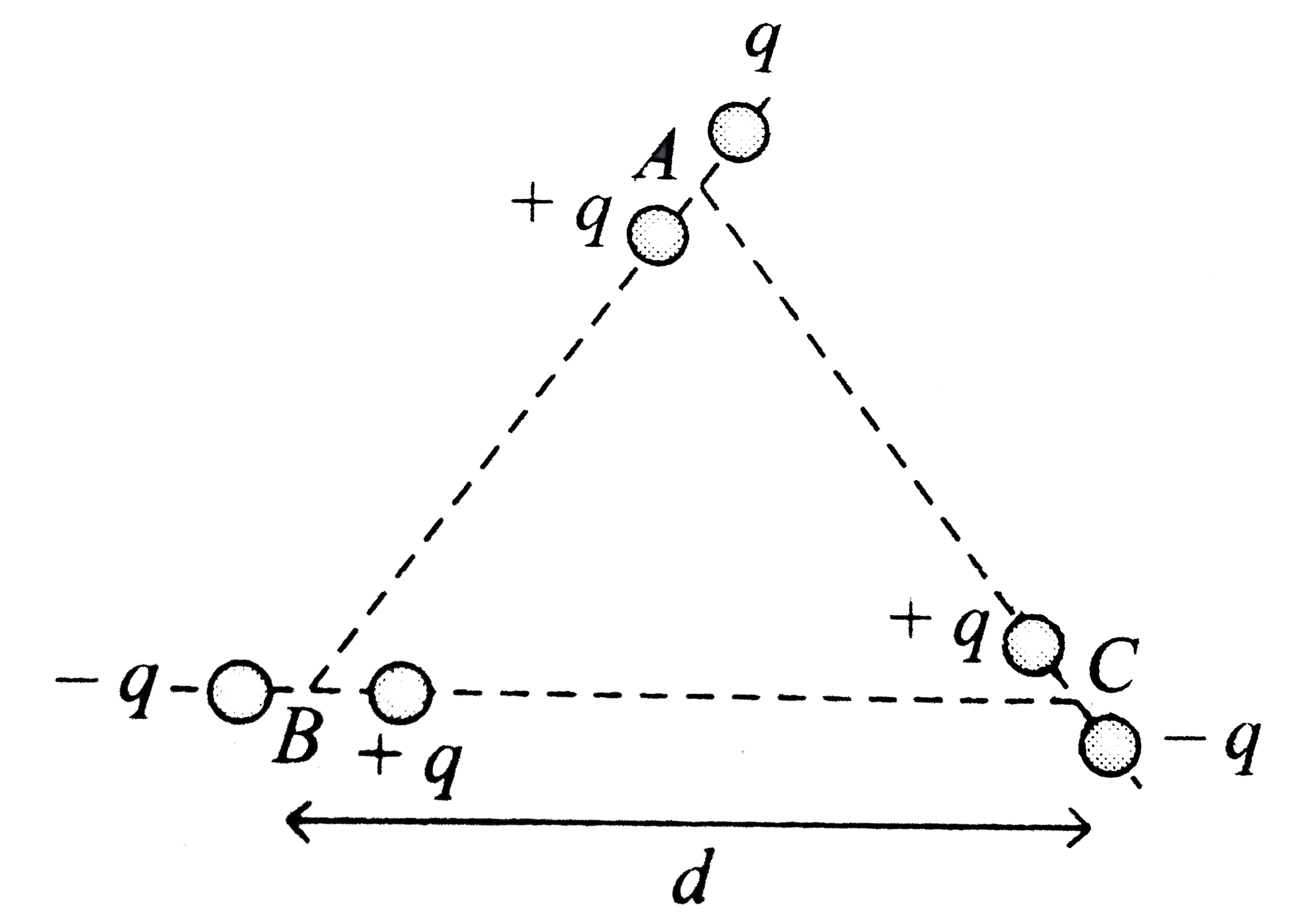 .
.
View SolutionThree point charges of +2q,+2qand−4q are placed at the corners A, B and C of an equilateral triangle ABC of side x. The magnitude of the electric dipole moment of this system is ?
View SolutionThree point charges 1C,2C and 3C are placed at the corners of an equilaternal triangle of side 1m. The work required to move these charges to the corners of a smaller equilaternal triangle of side 0.5m in two differenct ways as in fig. (A) and fig. (B) are Wa and Wb then:

View SolutionA common test to find the genotype of a hybrid is by
View SolutionThree charges of (+2q),(−q) and (−q) are placed at the corners A,B and C of an equilateral triangle of side a as shown in the adjoining figure. Then the dipole moment of this combination is
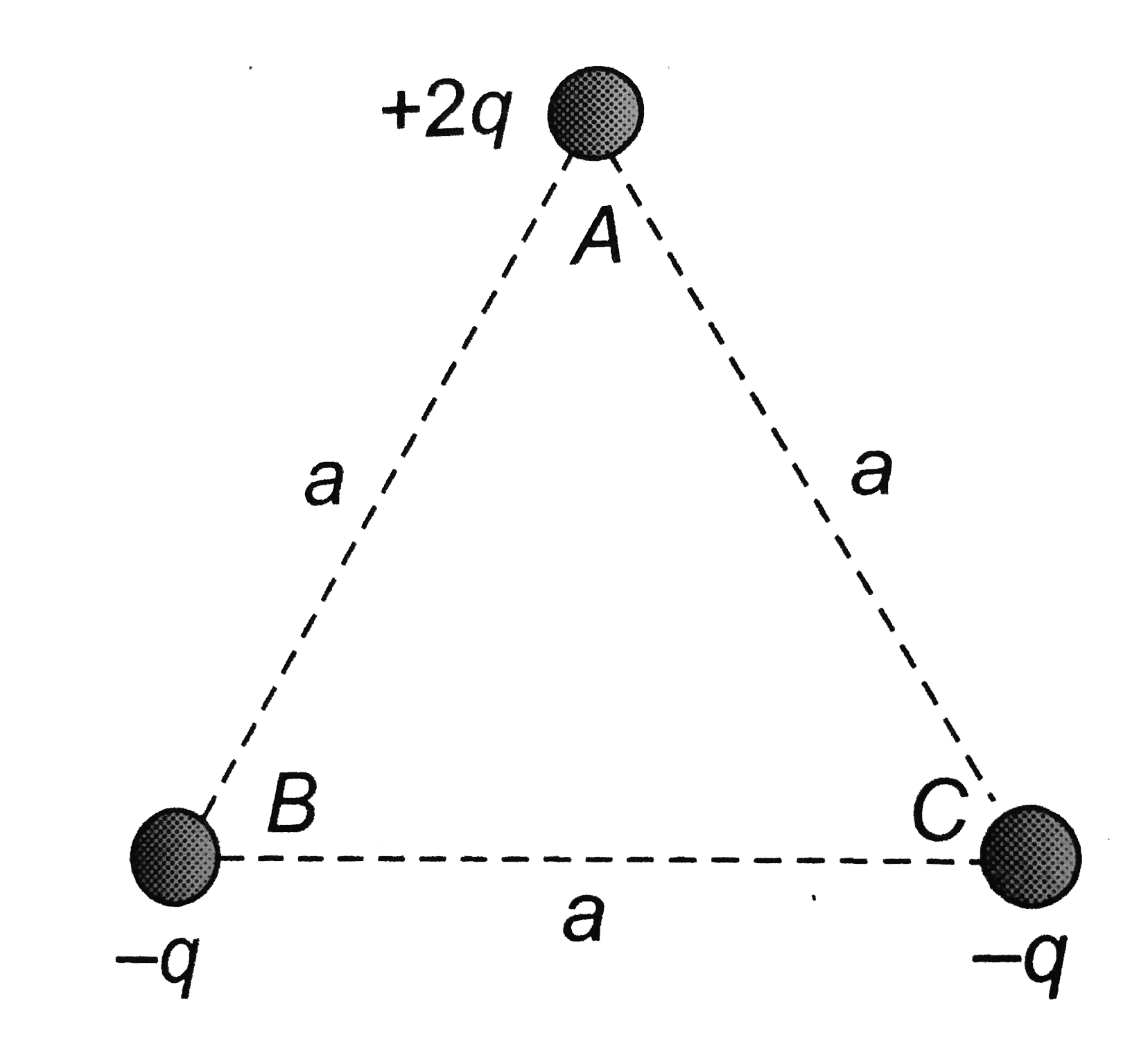
View SolutionA circle is inscribed in an equilateral triangle ABC of side 12 cm, touching its sides (Figure). Find the radius of the inscribed circle and the area of the shaded part.
View Solution
