Three identical stars of mass M form an equilateral triangle that rotates around the triangle's center as the stars move in a common circle about that center. The triangle has edge length L. What is the speed of the stars?
To find the speed of the stars rotating around the center of the equilateral triangle, we can follow these steps:
Step 1: Determine the distance from the center of the triangle to each star.
In an equilateral triangle, the center of mass (centroid) is located at a distance of L√3 from each vertex (star). This is derived from the geometry of the triangle.
Hint: Use the properties of an equilateral triangle to find the centroid's position.
Step 2: Write the expression for the centripetal force.
The centripetal force required to keep each star moving in a circular path is given by:
Fc=Mv2r
where M is the mass of each star, v is the speed of the stars, and r is the radius of the circular path, which we found to be L√3.
Hint: Remember that centripetal force is necessary for circular motion and depends on the mass, speed, and radius.
Step 3: Calculate the gravitational force between the stars.
The gravitational force Fg between any two stars can be expressed using Newton's law of gravitation:
Fg=GM2L2
where G is the gravitational constant, and L is the distance between the stars.
Hint: Use the formula for gravitational force and remember that there are two pairs of stars exerting gravitational forces on each other.
Step 4: Find the net gravitational force acting on one star.
Since there are two other stars exerting gravitational force on one star, we need to find the resultant force from these two. The angle between the forces is 60∘ (the angle in an equilateral triangle). The resultant gravitational force Fresultant can be calculated using the law of cosines:
Fresultant=√F2g+F2g+2FgFgcos(60∘)=√F2g+F2g+F2g=√3Fg
Thus,
Fresultant=√3⋅GM2L2
Hint: Use vector addition to find the resultant force from two equal forces at an angle.
Step 5: Set the centripetal force equal to the net gravitational force.
For the stars to maintain their circular motion, the centripetal force must equal the net gravitational force:
Mv2L√3=√3⋅GM2L2
Hint: Equate the expressions for centripetal force and gravitational force to find the relationship between speed and other variables.
Step 6: Solve for the speed v.
Rearranging the equation gives:
Mv2=√3⋅GM2L2⋅L√3
This simplifies to:
v2=GML
Taking the square root gives:
v=√GML
Hint: Simplify the equation carefully to isolate v.
Final Result:
The speed of each star is:
v=√GML
In an equilateral triangle, the center of mass (centroid) is located at a distance of L√3 from each vertex (star). This is derived from the geometry of the triangle.
The centripetal force required to keep each star moving in a circular path is given by:
Fc=Mv2r
where M is the mass of each star, v is the speed of the stars, and r is the radius of the circular path, which we found to be L√3.
The gravitational force Fg between any two stars can be expressed using Newton's law of gravitation:
Fg=GM2L2
where G is the gravitational constant, and L is the distance between the stars.
Since there are two other stars exerting gravitational force on one star, we need to find the resultant force from these two. The angle between the forces is 60∘ (the angle in an equilateral triangle). The resultant gravitational force Fresultant can be calculated using the law of cosines:
Fresultant=√F2g+F2g+2FgFgcos(60∘)=√F2g+F2g+F2g=√3Fg
Thus,
Fresultant=√3⋅GM2L2
For the stars to maintain their circular motion, the centripetal force must equal the net gravitational force:
Mv2L√3=√3⋅GM2L2
Rearranging the equation gives:
Mv2=√3⋅GM2L2⋅L√3
This simplifies to:
v2=GML
Taking the square root gives:
v=√GML
The speed of each star is:
v=√GML
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - GRAVITATIONEXERCISE - PRACTICE QUESTIONS (SINGLE CORRECT CHOICE TYPE)16videos
GRAVITATION
- BOOK - RESNICK AND HALLIDAYCHAPTER - GRAVITATIONEXERCISE - PRACTICE QUESTIONS (MORE THAN ONE CORRECT CHOICE TYPE)7videos
GRAVITATION
- BOOK - RESNICK AND HALLIDAYCHAPTER - GRAVITATIONEXERCISE - CHECKPOINT5videos
GRAVITATION
- BOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFRACTIONEXERCISE - Practice questions(Integers)4videos
GEOMETRICAL OPTICS : REFRACTION
- BOOK - RESNICK AND HALLIDAYCHAPTER - HEAT-MEASUREMENT AND TRANSFEREXERCISE - PRACTICE QUESTIONS( INTEGER TYPE)5videos
HEAT-MEASUREMENT AND TRANSFER
Similar Questions
If the latus rectum of a hyperbola forms an equilateral triangle with the vertex at the center of the hyperbola ,then find the eccentricity of the hyperbola.
View SolutionThree identical roads each of mass M and L are joined to form an equilateral triangle. Find the M.I. about an axis perpendicular to the plane of triangle and passing through
(a) center of triangle
(b) mid-point of a rod and
(c ) one vertex of triangle.View Solution
Knowledge Check
- Question 1 - Select One
Three identical stars, each of mass M, from an equilateral triangle (stars are positioned at the corners) that rotates around the centre of the triangle. The system is isolated and edge length of the triangle is L. The amount of work done, that is required ot dismantle the system, is:
A3GM2LB32GM2LC34GM2LDGM22L - Question 2 - Select One
Three identical rods, each of mass m and length l, form an equaliteral triangle. Moment of inertia about one of the sides is
 Aml26Bml2C3ml24D2ml23
Aml26Bml2C3ml24D2ml23 - Question 3 - Select One
Three particles each of mass m are kept at the vertices of an euilateral triangle of side L. The gravitational field at the centre due to these particle is
A−3GMLB−√3GMLC−3√3GMLD−GM3√3L
Magnetic field at center of an equilateral triangle of side length 9cm having current 2A is
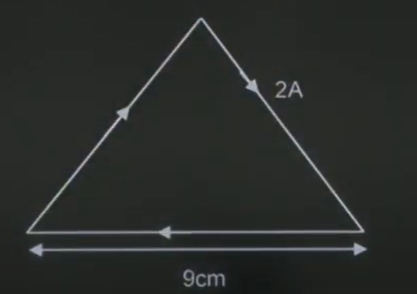 View Solution
View SolutionThree rods are arranged in the form of an equilateral triangle. Calculate the M.I. about an axis passing through the geometrical centre and perpendicular to the plane of the triangle (Assume that mass and length of each rod is M and L respectively).
View SolutionAn equilateral triangle circumscribes all the three circles each of radius 1 cm . What is the perimeter of the equilateral triangle ?
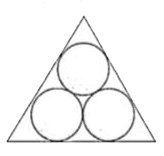 View Solution
View SolutionThree identical bar magnets each of magnetic moment M are placed in the form of an equilateral triangle as shown.
 View Solution
View SolutionAn isolated triple star systerm consists of two identical stars, each of mass m and f fixed star of mass M. They revolve around the central star in the same circular orbit to radius r. The orbiting stars are always at opposite ends of a diameter of the orbit. The time period of revolution of each star around the fixed is equal to:
 View Solution
View Solution

