Three indentical bodes of mass M are locatd at the verticles of an equailateral triangle of side L they revolve undr the effect of mutual gravitational force in a circular orbit circumscibing the traingle while preserving the equilateral triangle their orbital velocity is
√GML
√3GM2L
√3GML
√2GM3L
The correct Answer is:A
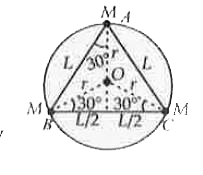
From the figure , L2=rcos30∘=√32r or r=L√3
The net force of attraction on mass at A due to masses at B and C is
FA=2[GM2L2]cos30∘=[GM2L2√3]
As this force provides the necessary centripetal force,
∴Mv2r=GM2L2√3 or Mv2√3L=GM2√3L2∴v=√GML
Topper's Solved these Questions
- GRAVITATIONBOOK - MTG GUIDECHAPTER - GRAVITATIONEXERCISE - NEET CAFE TOPICWISE PRACTICE QUESTIONS (ACCELERATION DUE TO GRAVITY AND ITS VARIATION WITH ALTITUDE AND DEPTH)
19 Videos
- GRAVITATIONBOOK - MTG GUIDECHAPTER - GRAVITATIONEXERCISE - NEET CAFE TOPICWISE PRACTICE QUESTIONS (GRAVITATIONAL POTENTIAL ENERGY AND GRAVITATIONAL POTENTIAL)
6 Videos
- GRAVITATIONBOOK - MTG GUIDECHAPTER - GRAVITATIONEXERCISE - NEET CAFE TOPICWISE PRACTICE QUESTIONS (KEPLER.S LAWS OF PLANETARY MOTION)
9 Videos
- BEHAVIOUR OF PERFECT GAS AND KINETIC THEORYBOOK - MTG GUIDECHAPTER - BEHAVIOUR OF PERFECT GAS AND KINETIC THEORYEXERCISE - AIPMT / NEET (MCQs)
11 Videos
- KINEMATICS BOOK - MTG GUIDECHAPTER - KINEMATICS EXERCISE - AIPMT/ NEET MCQs
31 Videos
Similar Questions
Three particles each of mass m=1 kg, are located at the vertices of an equilateral triangle of side a =4m. The speed at which they must move to revolve in a circular orbit, under the inluence of mutual gravitational force, circumscribing and preserving the equilateral triangle is v=n√G, then the value of n is
View SolutionIf two particles each of mass m are placed at the two vertices of an equilateral triangle of side a, then the resultant gravitational force on mass m placed at the third vertex is
View Solution
Knowledge Check
Three particle each of mass m, are located at the vertices of an equilateral triangle of side a. At what speed must they move if they all revolve under the influence of their gravitational force of attraction in a circular orbit circumscribing the triangle while still preserving the equilateral triangle ?
 A√GmaB√2GmaC√3GmaD√4Gma
A√GmaB√2GmaC√3GmaD√4GmaThree mass ‘m’ each are kept at corner of a equilateral triangle and are rotating under effect of mutual gravitational force -
ARadius of circular path followed by mass is a/2BVelocity of mass is √GmaCBinding energy of system is 1.5Gm2aDTime period of mass is √πa32GmThree particles of equal mass 'm' are situated at the vertices of an equilateral triangle of side L. The work done in increasing the side of the triangle to 2L is
A2G2m2LBGm22LC3Gm22LD3Gm2L
Four identical particles of mass M are located at the corners of a square of side ‘a’. What should be their speed if each of them revolves under the influence of others’ gravitational field in circular orbit circumscribing the square ?

View SolutionThree point masses 'm' each are placed at the three vertices of an equilateral traingle of side 'a'. Find net gravitational force on any point mass.
View SolutionThree particles each of mass m are kept at the vertices of an euilateral triangle of side L. The gravitational field at the centre due to these particle is
View SolutionThree particles each of mass m are kept at the vertices of an euilateral triangle of side L. The gravitational field at the centre due to these particle is
View SolutionThree particles each of mass m are kept at vertices of an equilateral triangle of side L. The gravitational field at centre due to these particle is
View Solution
