Three particles of masses 1.0 kg 2.0 kg and 3.0 kg are placed at the corners A,B and C respectively of an equilateral triangle ABC of edge 1m. Locate the centre of mass of the system.
To find the center of mass of the system of three particles located at the corners of an equilateral triangle, we can follow these steps:
Step 1: Define the coordinates of the particles
Let's assign coordinates to the corners of the equilateral triangle ABC:
- Mass m1=1.0kg at point A (0, 0)
- Mass m2=2.0kg at point B (0.5, √32) since the height of the triangle is √32 when the base is 1 meter.
- Mass m3=3.0kg at point C (1, 0)
Step 2: Calculate the total mass
The total mass M of the system is:
M=m1+m2+m3=1+2+3=6kg
Step 3: Calculate the x-coordinate of the center of mass
The x-coordinate xcm of the center of mass is given by the formula:
xcm=m1x1+m2x2+m3x3M
Substituting the values:
xcm=(1⋅0)+(2⋅0.5)+(3⋅1)6
Calculating:
xcm=0+1+36=46=23m
Step 4: Calculate the y-coordinate of the center of mass
The y-coordinate ycm of the center of mass is given by:
ycm=m1y1+m2y2+m3y3M
Substituting the values:
ycm=(1⋅0)+(2⋅√32)+(3⋅0)6
Calculating:
ycm=0+√36=√36m
Step 5: Final coordinates of the center of mass
Thus, the coordinates of the center of mass of the system are:
(23,√36)m
Summary
The center of mass of the three particles is located at:
(23,√36)m
Let's assign coordinates to the corners of the equilateral triangle ABC:
- Mass m1=1.0kg at point A (0, 0)
- Mass m2=2.0kg at point B (0.5, √32) since the height of the triangle is √32 when the base is 1 meter.
- Mass m3=3.0kg at point C (1, 0)
The total mass M of the system is:
M=m1+m2+m3=1+2+3=6kg
The x-coordinate xcm of the center of mass is given by the formula:
xcm=m1x1+m2x2+m3x3M
Substituting the values:
xcm=(1⋅0)+(2⋅0.5)+(3⋅1)6
Calculating:
xcm=0+1+36=46=23m
The y-coordinate ycm of the center of mass is given by:
ycm=m1y1+m2y2+m3y3M
Substituting the values:
ycm=(1⋅0)+(2⋅√32)+(3⋅0)6
Calculating:
ycm=0+√36=√36m
Thus, the coordinates of the center of mass of the system are:
(23,√36)m
The center of mass of the three particles is located at:
(23,√36)m
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Question For short Answer
25 Videos
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective -2
11 Videos
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective -1
18 Videos
- CALORIMETRYBOOK - HC VERMA ENGLISHCHAPTER - CALORIMETRYEXERCISE - Short answer
9 Videos
- CIRCULAR MOTIONBOOK - HC VERMA ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Question for short Answer
10 Videos
Similar Questions
Three particles of masses 1kg, 2kg and 3kg are placed at the corners A, B and C respectively of an equilateral triangle ABC of edge 1m. Find the distance of their centre of mass from A.
View SolutionFour particles of masses 1kg,2kg,3kg and 4kg are placed the four vertices A,B,C and D, respectively, of a square of side 1m. Find the position of centre of mass of the particles.
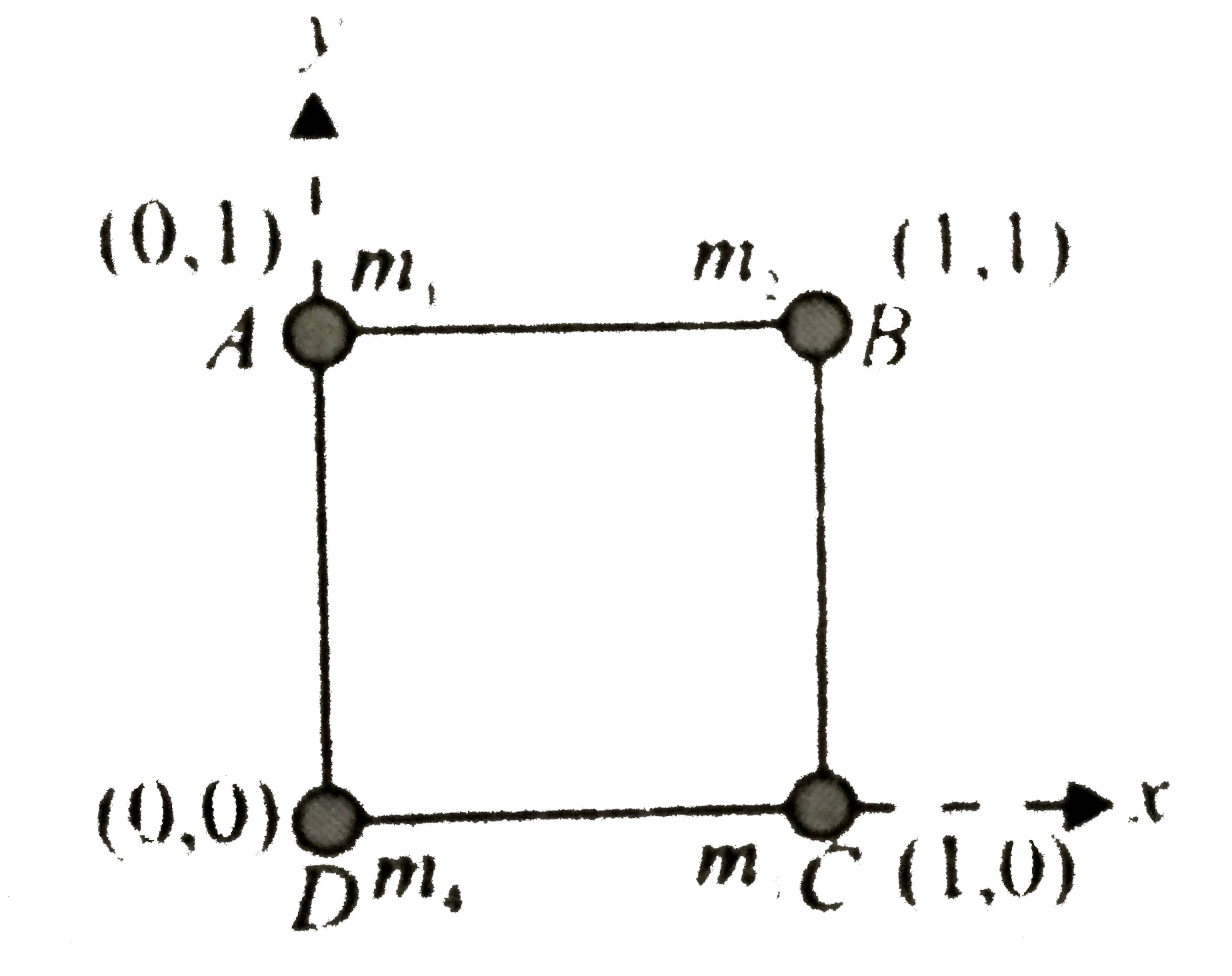
View Solution
Knowledge Check
Three particles of masses 1kg,32kg,and2kg are located the vertices of an equilateral triangle of side a. The x,y coordinates of the centre of mass are.
Aa. 5a9,2a3√3Bb. 2a3√3,5a9Cc. 5a9,2a√3Dd. 2a√3,5a9
Three point particles of masses 1.0 kg, 1.5 kg and 2.5 kg are placed at three corners of a right angle triangle as shown in figure. The centre of mass of the system is at a point :
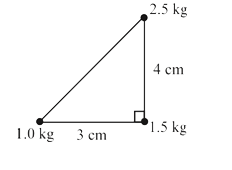
View SolutionThree point particles of masses 1.0 kg, 1.5 kg and 2.5 kg are placed at three corners of a right angle triangle as shown in figure. The centre of mass of the system is at a point :

View SolutionThree balls of masses 1kg,2kgand3kg are arranged at the corners of an equilateral triangle of side 1m. What will be the moment of inertia of the system and perpendicular to the plane of the triangle.
View Solution4 Masses 8 kg, 2 kg, 4 kg and 2 kg are placed at the corners A, B, C, D respectively of a square ABCD of diagonal 80 cm. The distance of centre of mass from A will be
View SolutionThree particles of masses 0.50 kg, 1.0 kg and are placed at the corners of a right angle triangle, as shown in fig. Locate the centre of mass of the system.
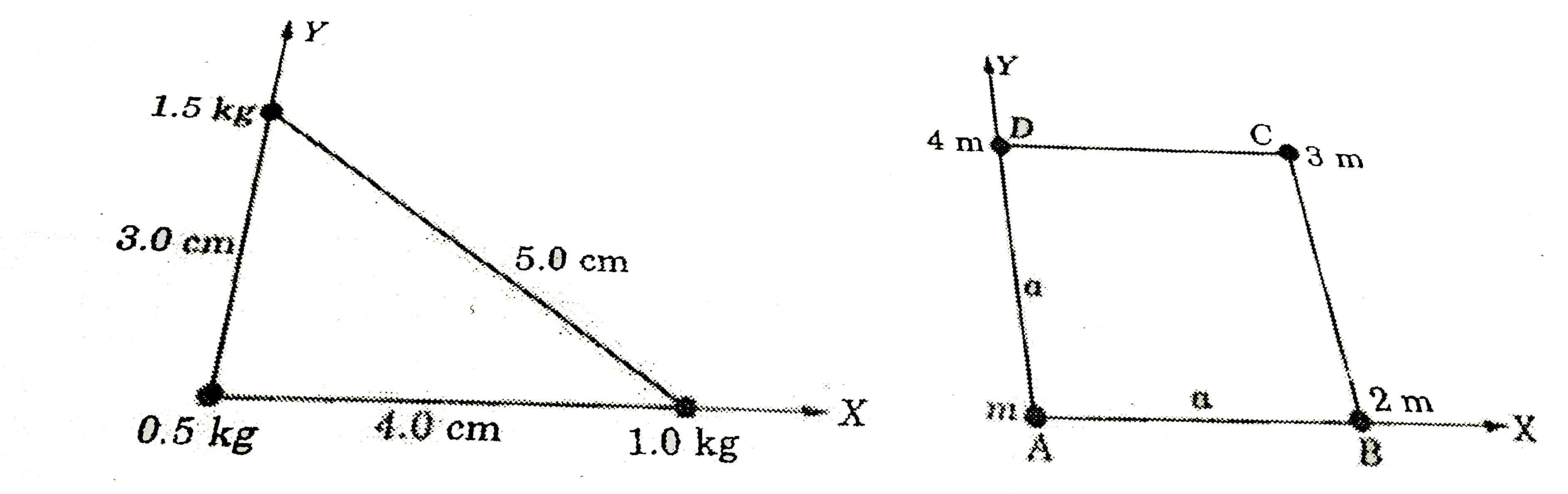
View SolutionThree point particles of masses 1.0 kg 2 kg and 3 kg are placed at three comers of a right angle triangle of sides 4.0 cm , 3.0 cm and 5.0 cm as shown in the figure . The centre of mass of the system is at point :

View SolutionThree point particles of masses 1.0 kg 2 kg and 3 kg are placed at three comers of a right angle triangle of sides 4.0 cm , 3.0 cm and 5.0 cm as shown in the figure . The centre of mass of the system is at point :

View Solution
