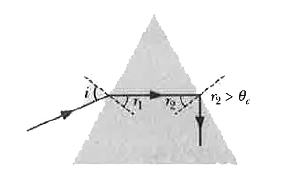
Total internal reflection in a prism
What is the relationship between A and n so, that no rays come out of second face ?

(1) Here we want to choose the refractive index of the prism such that a ray will always undergo total internal reflection . Note that this total internal reflection can occur only when the light ray goes from denser to rarer medium. In other words, this will occur only when the ray is incident on the second surface.
(2) The situation implies that for the smallest angle r2 also, the total internal reflection should occur.
(3) r1+r2=A. So, when r2 is minimum r1 is maximum. The angle of incidence i is also maximum by Snell.s law. But the maximum angle of incidence can be 90∘. This problem implies that if a total internal reflection occurs when angle of incidence is 90∘, then total internal reflection will occur at all the angles
Calculation : Applying Snell.s law at the first surface
1×sin90∘=nsinr1
r1=sin−1(1n)
r2=A−sin−1(1n)
But for total internal reflection at the second surface :
r2>θc
sinr2>1sinθc(1n)
A−sin−1(1n)>sin−1(1n)
Thus, the condition becomes
n>cosec(A2).
Note : Many optical instruments such as binoculars periscopes, and telescopes, use glass prisms and total internal reflection to turn a beam of light through 90∘ or 180∘.
Topper's Solved these Questions
- GEOMETRICAL OPTICS : REFRACTIONBOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFRACTIONEXERCISE - Check point
6 Videos
- GEOMETRICAL OPTICS : REFRACTIONBOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFRACTIONEXERCISE - Problems
44 Videos
- GEOMETRICAL OPTICS : REFLECTION BOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFLECTION EXERCISE - PRACTICE QUESTIONS (Integer Type)
3 Videos
- GRAVITATIONBOOK - RESNICK AND HALLIDAYCHAPTER - GRAVITATIONEXERCISE - PRACTICE QUESTIONS (INTEGER TYPE)
4 Videos
Similar Questions
Knowledge Check
A ray of light is incident at an angle of 50∘ on one face of an equilateral prism . What is the angle ,which the emergent ray makes with the second face of the prism , if the deviation produced by the prism is 42∘ ?
A48∘B38∘C58∘D42∘A total reflecting equilateral prism can be used to deviate a ray of light through :
A30∘B60∘C75∘D90∘
The path of a ray of light passing through an equilateral glass prism ABC is shown in figure. The ray of light is incident on face BC at the critical angle for just total internal reflection. The total internal reflection. The total angle of deviation after the refraction at face AC is 108∘. Calculate the refractive index of the glass.
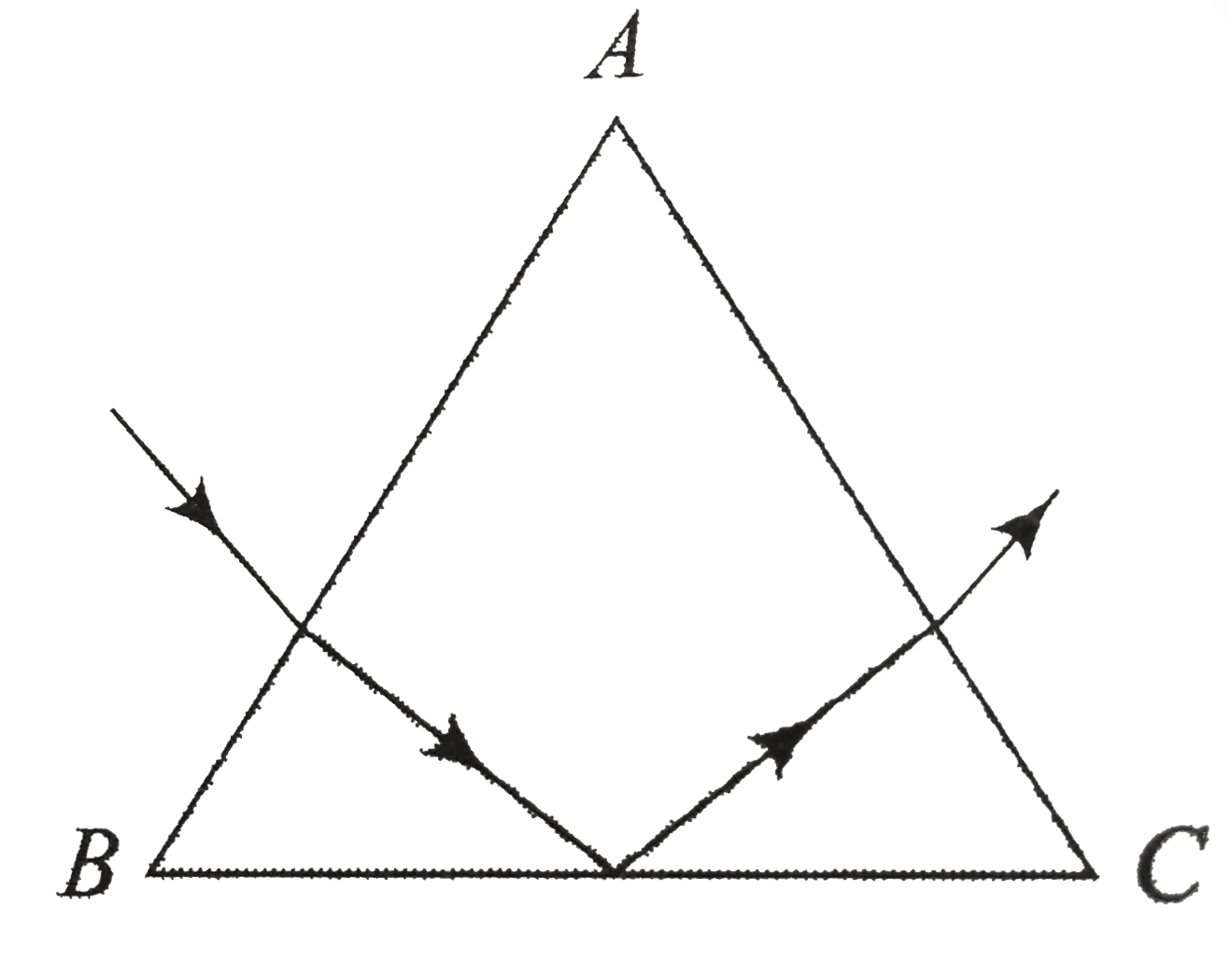
View SolutionThe path of a ray of light passing through an equilateral glass prism ABC is shown in figure. The ray of light is incident on face BC at the critical angle for just total internal reflection. The total internal reflection. The total angle of deviation after the refraction at face AC is 108∘. Calculate the refractive index of the glass.

View SolutionState the conditions under which total internal reflection occurs. One face of a prism with a refracting angle of 30∘ is coated with silver. A ray incident on another face at an angle of 45∘ is refracted and reflected from the silver coated face and retraces its path. Find the refractive index of the material of the prism.
View SolutionA ray of light is incident on a glass prism of refractive index μ and refractive angle A. If it just suffers total internal reflection at the other face, obtain an expression relating the angle of incidence , angle of prism and critical angle.
View SolutionA ray of light is incident on a glass prism of refractive index μ and refractive angle A. If it just suffers total internal reflection at the other face, obtain an expression relating the angle of incidence , angle of prism and critical angle.
View SolutionWhat is total internal reflection of light ? What are conditions for total internal reflection ?
View Solution
