Twelve identical capacitors of capacitance C are connected across each edge of a cube. Find equivalent capacitance across one of the edges.
Video Solution
Text Solution
Refer to the figure for charge distribution. We have to calculate effective capacitance between points A and D. Let us suppose that a battery of potential difference V is connected between these two points.
We know that if Q is the total charge supplied by the battery to the network of capacitors then equivalent capacitance will be Q/V.
Capacitor connected between points A and D is in parallel with the rest of the circuit. In case we do not include it in calculation then we can add it to the answer of remaining network in parallel later. Nevertheless we have included it in charge distribution.
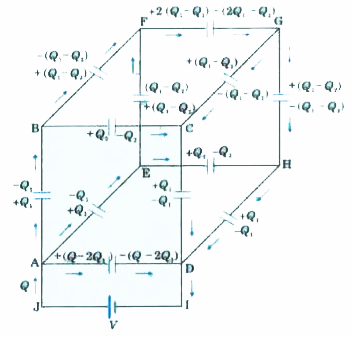
Branches AE and AB are similarly connected to the point A. Hence we have taken equal charges Q1 for capacitors connected to both of them. Branches BC and EH are also identical so we have taken the same charge Q2 for capacitors in these two branches. Moreover the whole network is in symmetric halves between the two terminals of a battery. That is why we can see symmetry in charge distribution for left and right parts of the network except reverse polarity is used on both sides. Rest of the charge distribution is self-explanatory.
Let us apply Kirchhoff.s law for loop IJAEHDI:
V−Q1C−Q2C−Q1C=0⇒2Q1+Q2=CV ...(i)
Let us apply Kirchhoff.s law for loop HEFGH:
Q2C−Q1−Q2C−2Q1−Q2C−Q1−Q2C−0
⇒Q2C=4(Q1−Q2)C⇒Q2=4Q1−4Q2
⇒4Q1=5Q2⇒Q2=4Q15 ...(ii)
Now substituting Q2 from equation (ii) in equation (i) we get the following:
2Q1+4Q15=CV⇒Q1=5CV14 ...(iii)
Let us apply Kirchhoff.s law for loop IJADI:
V−Q−2Q1C=0
Q−2Q1=CV ...(iv)
Substituting Q1 from equation (iii) in equation (iv) we get the following:
Q−2(5CV14)=CV⇒Q=57CV+CV
⇒QV=127C⇒Ceq=127C
Alternate solution:
The moment we get to know that capacitors of branches AE and AB carry the same charge then due to same capacitance we can say that potential of points B and E must be same due to the similar potential difference across both the capacitors. Using the same logic we can say that points C and H must also be at the same potential. Points of same potential can be assumed as points at same location and circuit can be redrawn as follows:
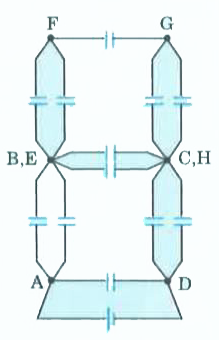
We know that capacitances of all the capacitors are C in the above redrawn network of capacitors. The network can be solved for equivalent capacitance between points A and D using method of series and parallel combinations. Following are the steps to arrive at the same answer using this alternate method.
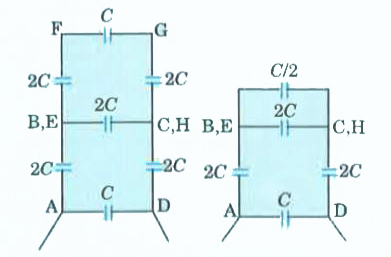
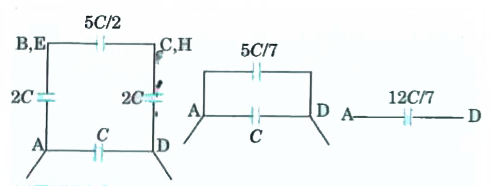
|
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - NCERT FILE Solved (Textbook Exercise)
11 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - NCERT FILE Solved (Additional Exercises)
23 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Conceptual Questions
37 Videos
- ELECTROMAGNETIC WAVESBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - CHAPTER PRACTICE TEST
14 Videos
- MAGNETISM AND MATTERBOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
16 Videos
Similar Questions
Knowledge Check
Find the equivalent capacitance across A&B
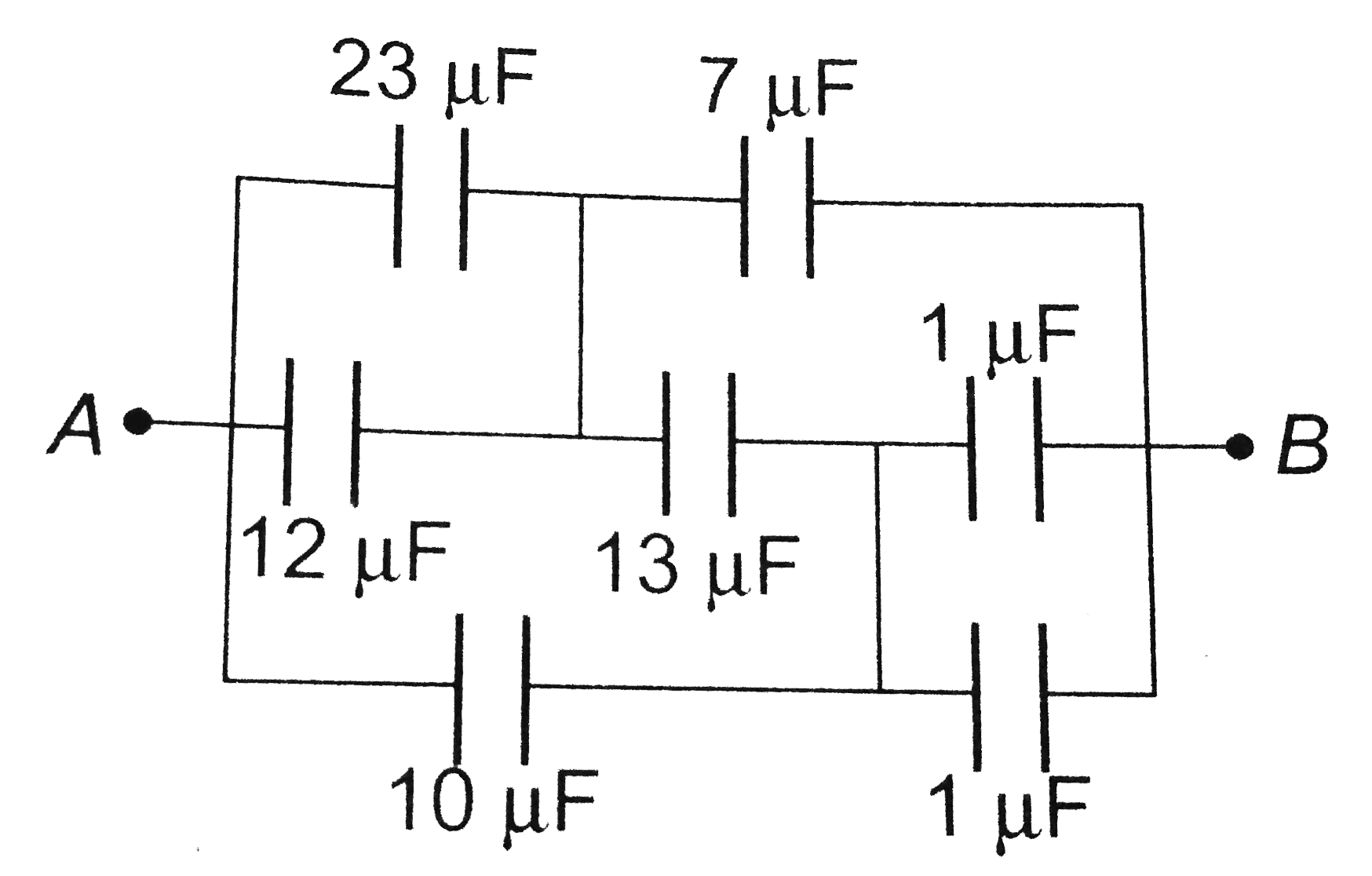 A283μFB152μFC15μFDNone
A283μFB152μFC15μFDNoneFind the equivalent capacitance across A and B.
 .A356μFB256μFC15μFDnone of these
.A356μFB256μFC15μFDnone of theseThere are 10 identical capacitors each of capacitance C.
AIf all of them are connected in series, their equivalent capacitance is C/10BIf all of them are connected in parallel, their equivalent capacitance is 10CCIf two series combinations each having 5 capacitors are connected in parallel, their equivalent capacitance is 2C/5DIf they are connected as five parallel combinations each one having two capacitors in series, their equivalent capacitance is 5C/2.
Find the equivalent capacitance across points A and B.
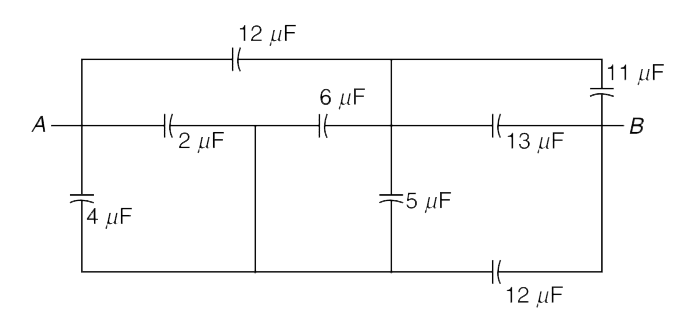
View SolutionTwelve capacitors, each having a capacitance C, are connected to form a cube . Find the equivalent capacitance between the diagonally opposite corners such as A and B.

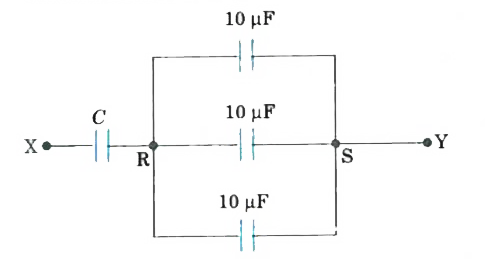
View SolutionThree identical 10 μF capacitors and a capacitor of capacitance C are connected as shown in the figure. Find the capacitance C if the equivalent capacitance between X and Y is 20μF.
View SolutionThree equal capacitors, each with capacitance C are connected as shown in figure. Then the equivalent capacitance between A and B is
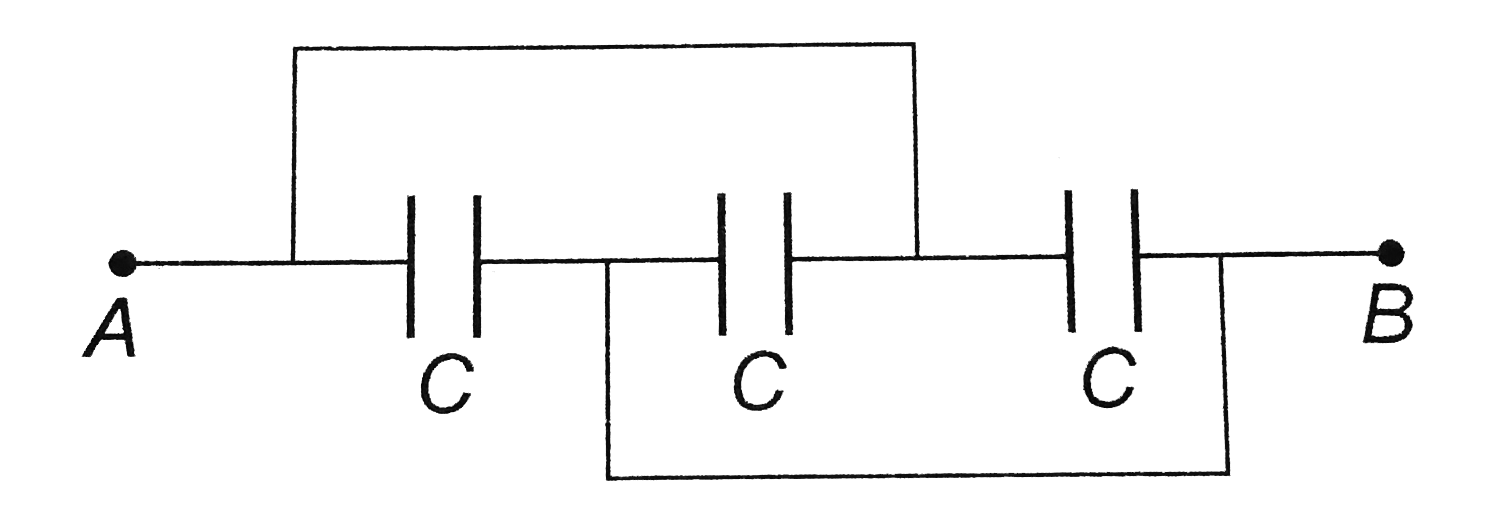
View SolutionAn infinite number of identical capacitors each of capacitance 1mF are connected as shown in the figure. Then the equivalent capacitance between A and B is.
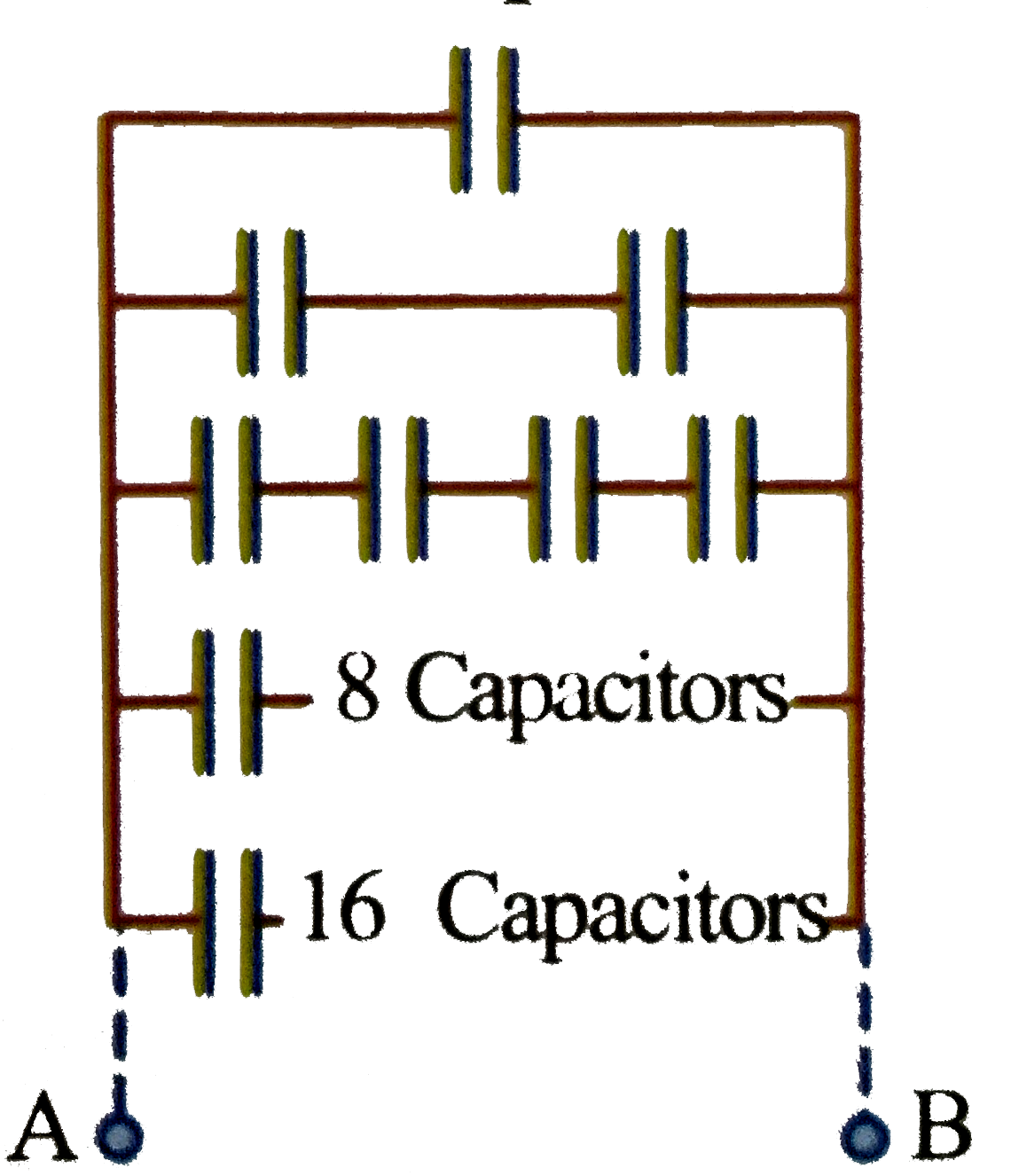 .
.
View Solution