Question

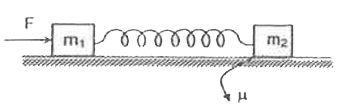
Two block of masses $m_1$ and $m_2$ connected by a light spring rest on a horizontal plane. The coefficient of friction between the block and the surface is equal to $\mu$. What minimum constant force has to be applied in the horizontal direction to the block of mass $m_1$ in order to shift the other block?

Options

A. 8 N
B. 15 N
C. 10 N
D. 25 N

Answer

A

Explanation

To solve the problem of determining the minimum constant force $$F$$ that must be applied to block $$m_1$$ in order to shift block $$m_2$$, we can follow these steps:

1. Understanding the Forces:
- Block \( m_1 \) is connected to block \( m_2 \) by a light spring. The coefficient of friction between both blocks and the surface is \( \mu \).
- The force \( F \) is applied to block \( m_1 \) in the horizontal direction.

2. Identifying the Condition for Block \( m_2 \) to Move:
- For block \( m_2 \) to start moving, the force exerted by the spring on block \( m_2 \) (let's denote it as \( kx \), where \( k \) is the spring constant and \( x \) is the extension of the spring) must overcome the frictional force acting on block \( m_2 \).
- The limiting frictional force \( f_{\text{friction}} \) on block \( m_2 \) is given by:
\( f_{\text{friction}} = \mu m_2 g \)

3. Setting Up the Equation:
- For block \( m_2 \) to start moving, we need:
\( kx \geq \mu m_2 g \)

4. Applying Work-Energy Principle:
- The work done by the applied force \( F \) must equal the work done against friction and the work done on the spring. The work-energy theorem states:
\( F \cdot x = f_{\text{friction}} \cdot x + \frac{1}{2} k x^2 \)
- Substituting \( f_{\text{friction}} \):
\( F \cdot x = \mu m_2 g \cdot x + \frac{1}{2} k x^2 \)

5. Simplifying the Equation:
- Dividing through by \( x \) (assuming \( x \neq 0 \)):
\( F = \mu m_2 g + \frac{1}{2} k x \)

6. Finding Minimum Force \( F \):
- To find the minimum force \( F \), we need to minimize the term \( kx \). The minimum value of \( kx \) occurs when \( kx = \mu m_2 g \) (from step 3).
- Substituting this back into the equation for \( F \):
\( F_{\text{min}} = \mu m_2 g + \frac{1}{2} \mu m_2 g = \frac{3}{2} \mu m_2 g \)

7. Final Expression:
- Therefore, the minimum constant force \( F \) that must be applied to block \( m_1 \) to shift block \( m_2 \) is:
\( F_{\text{min}} = \mu (m_1 + m_2) g \)