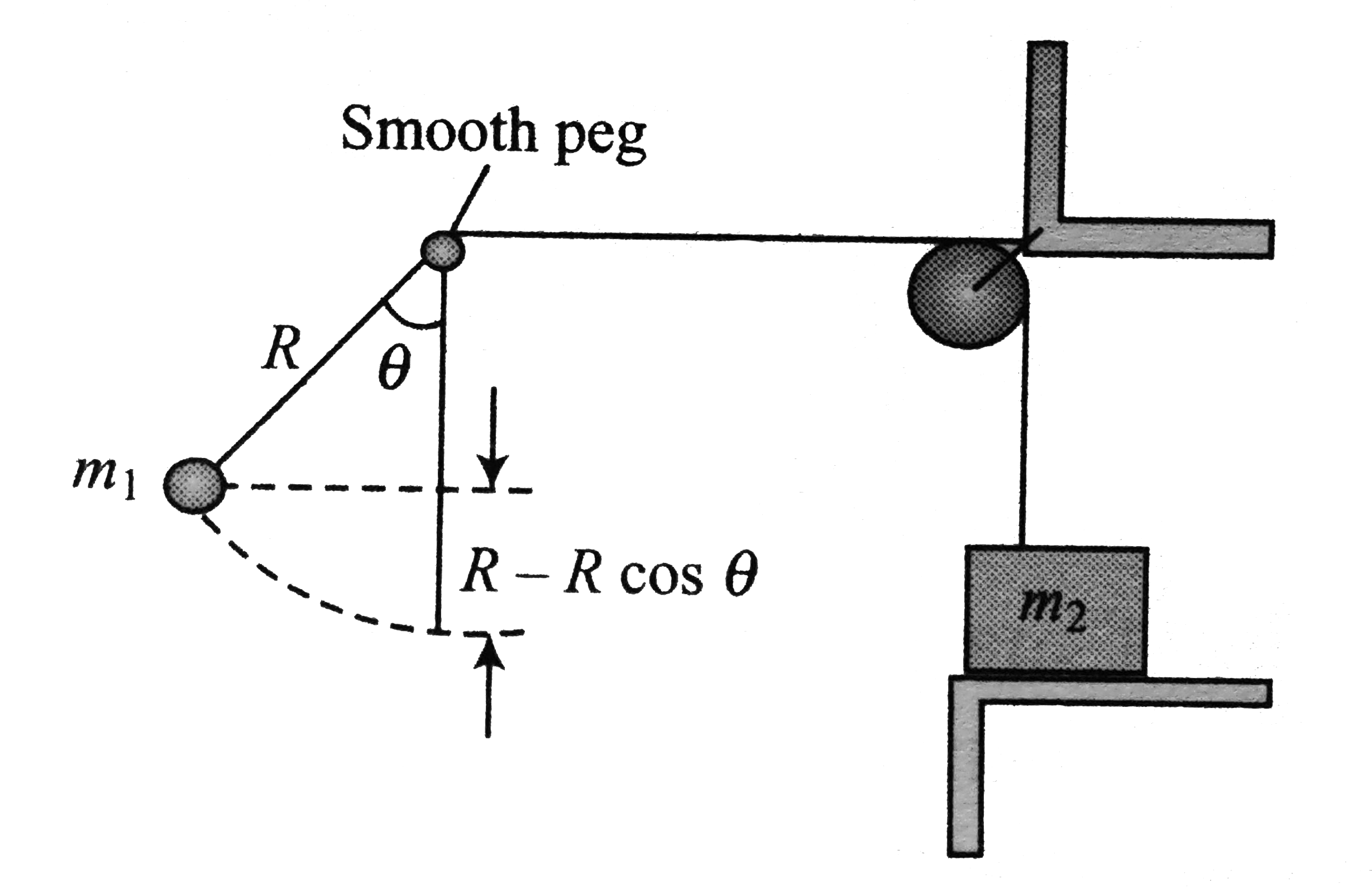
Two blocks are connected by a massless string that passes over a frictionless peg as shown in figure. One end of the string is attached to a mass m1=3kg, i.e., a distance R=1.20m from the peg. The other end of the string is connected to a block of mass m2=6kg resting on a table. From what angle θ, measured from the vertical, must the 3−kg block be released in order to just lift the 6kg block off the table?
The correct Answer is:60∘
This problem involves several concepts. First we will apply conservation of energy to find the speed of the block m1 at the bottom of the circular path as a function of θ and the radius of the path, R.
From Newton's second law we will determine the tension at the bottom of its path as function of given parameters. Finally, the block m2 will lift off the ground when the upward force (tension) exerted by the cord just exceeds the weight of the block. We take bottom of the circle as reference level.
From conservation of energy, we have
KEi+Ui=KEf+Uf
0+m1g(R−Rcosθ)=12m1v2+0
v2=2gR(1−cosθ) (i)
Applying Newton's second law on block of mass m2, we have
∑Fn=T−m1g=m1v2R
T=m1g+m1v2R (ii)
As the string is massless, tenstion T is constant throughout. When m2 just lifts off the normal reaction becomes zero. For block m2, we have
T=m2g (iii)
From Eqs. (i), (ii), and (iii), we get
m2g=m1g+m12gR(1−cosθ)R
cosθ=3m1−m22m1=3×3−62×3=12
θ=60∘
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Single Correct
100 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Multiple Correct
25 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.5
15 Videos
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
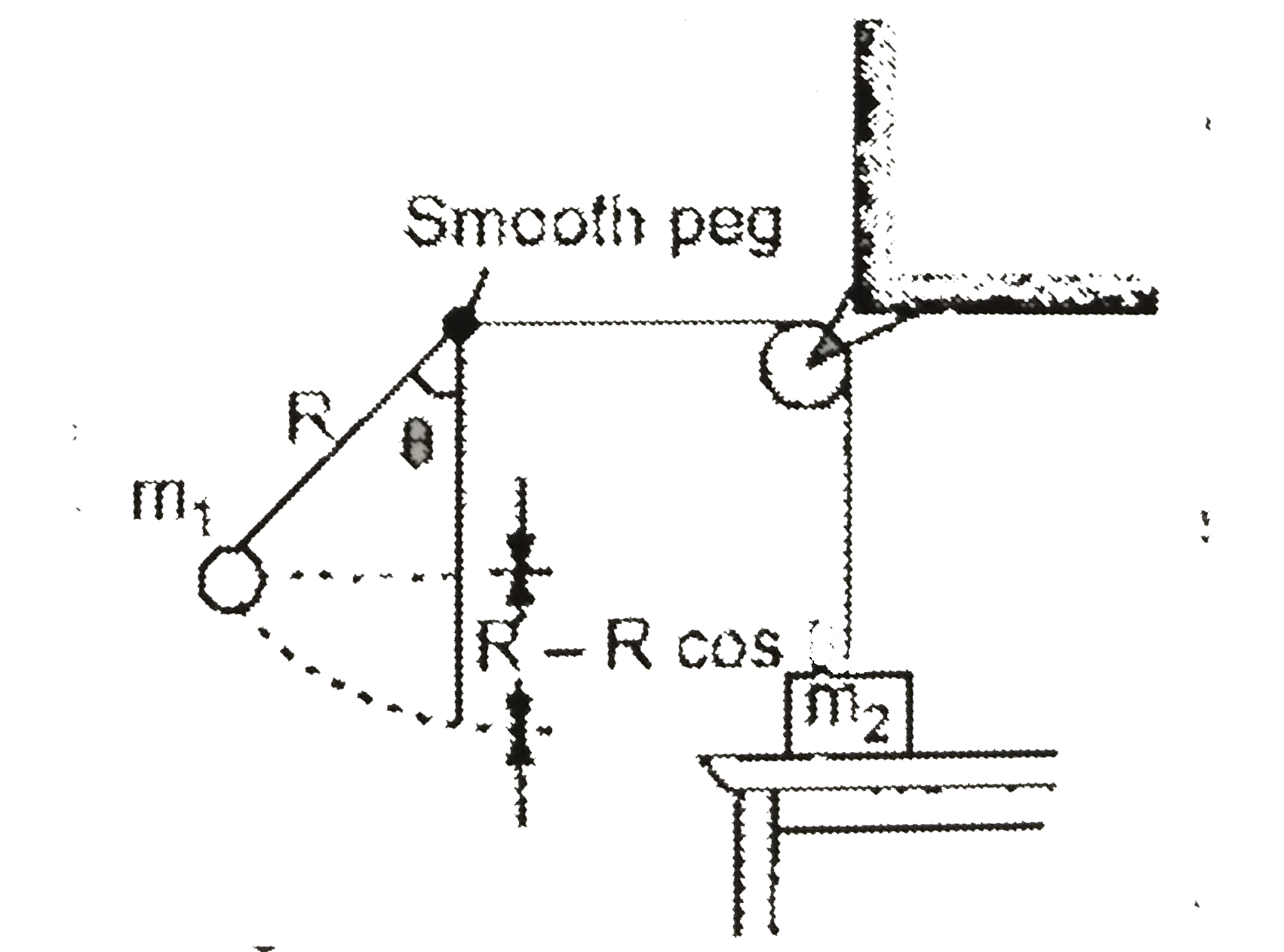
Two blocks are connected by a massless string that passes over a frictionless peg as shown in Fig. 3E.46. One end of the string is attached to a mass m1=3kg i.e. a distance R=1.20m from the peg. The other end of the string is connected to a block of mass m2=6kg resting on a table. From what angle θ, measured from the vertical, must the 3 kg block be released in order to just lift the 6 kg block off the table ?
View SolutionTwo masses 40kg and 30 kg connected by a massless string passing over a frictionless light pulley as shown in the figure. The tension ( almost ) in the string will be : ( All surfaces are frictionless)

View Solution
Knowledge Check
Two blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.
 A188 NB2=368 NC288 ND168 N
A188 NB2=368 NC288 ND168 NTwo blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.
 A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2Two blocks of masses 3 kg and 6 kg are connected by a string as shown in the figure over a frictionless pulley. The acceleration of the system is
 A4m/s2B2m/s2CzeroD6m/s2
A4m/s2B2m/s2CzeroD6m/s2
Two blocks of masses m1andm2(m1>m2) connected by a massless string passing over a frictionless pulley Magnitude of acceleration of blocks would be
View SolutionTwo bodies of masses 4 kg and 6 kg are tied to the ends of a massless string. The string passes over a frictionless pulley. The acceleration of the system is :
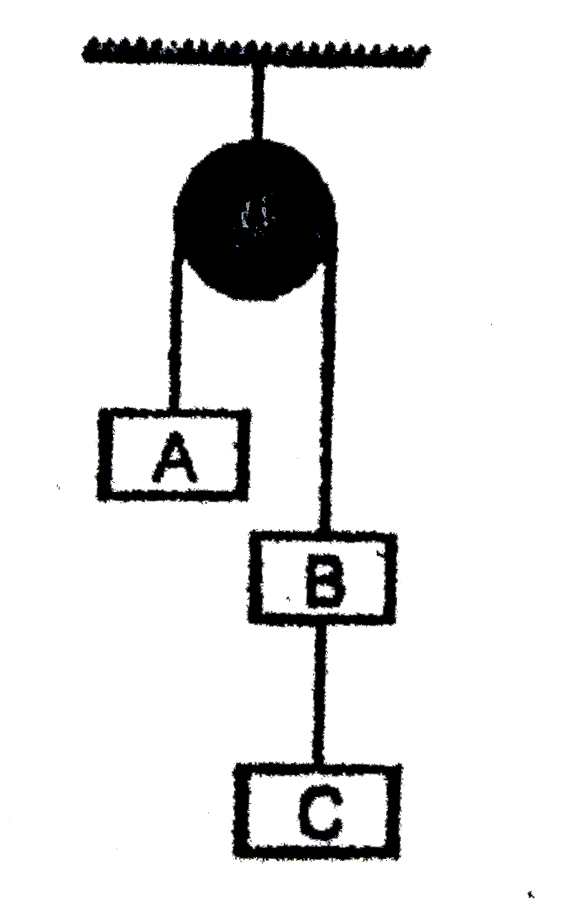
View SolutionThree blocks A,B and C of mass 10 kg each are hanging on a string passing over a fixed frictionless pulley as shown in figure. The tension in the string connecting blocks B and C is (g=10m/s2)
View SolutionTwo blocks of masses 10 kg and 20 kg are connected by a massless string and are placed on a smooth horizontal surface as shown in the figure. If a force F=600 N is applied to 10 kg block, then the tension in the string is

View SolutionTwo blocks A and B , each of mass 10kg , are connected by a light string passing over a smooth pulley as shown in the figure. Block A will remain at rest if the friction on it is

View Solution
