Two blocks each of mass M are connected to the ends of a light frame as shown in figure. The frame is rotated about the vertical line of symmetry. The rod breaks if the tension in it exceeds T0. Find the maximum frequency with which the frame may be rotted without breaking the rod.

Consider one of the blocks. If the frequencey of revolution is f, the angular velocity is ω=2πf. The acceleration towards the centre is v2l=ω2l=4π2f2l. The only horizontal force on the blck is the tension of the rod. At the point of breaking this foce is T0. So from Newton's second law
T0=M.4π2f2l
or f=12π[T0Ml]12
Topper's Solved these Questions
- CIRCULAR MOTIONBook:HC VERMA ENGLISHChapter:CIRCULAR MOTIONExercise:Objective -1
Explore 16 Videos
- CIRCULAR MOTIONBook:HC VERMA ENGLISHChapter:CIRCULAR MOTIONExercise:Objective -2
Explore 6 Videos
- CIRCULAR MOTIONBook:HC VERMA ENGLISHChapter:CIRCULAR MOTIONExercise:Question for short Answer
Explore 10 Videos
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBook:HC VERMA ENGLISHChapter:CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONExercise:Objective -2
Explore 11 Videos
- FLUID MECHANICSBook:HC VERMA ENGLISHChapter:FLUID MECHANICSExercise:All Questions
Explore 90 Videos
Similar Questions
A particle of mass 100 g tied to a string is rotated along the circle of radius 0.5 m. The breaking tension of the string is 10 N. The maximum speed with which particle can be rotated without breaking the string is
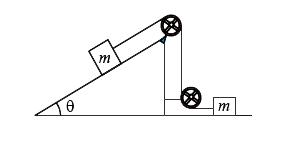
View SolutionTwo blocks each of mass m are connected over two light and frictionless pulleys and a fixed wedge by a light string as shown in figure. The tension in the string is :
View SolutionThe breaking tension of a string is 10 N. A particle of mass 0.1 kg tied to it is rotated along a horizontal circle of radius 0.5 meter. The maximum speed with which the particle can be rotated without breaking the string is
View SolutionTwo blocks each of the mass m are attached to the ends, a massless rod which pivots as shown in figure. Initial the rod is held in the horizontal position and then release, Calculate the net torque on this system above pivot.

View SolutionA block of mass m is connected to a spring of spring constant k as shown in figure. The frame in which the block is placed is given an acceleration a towards left. Neglect friction between the block and the frame walls. The maximum velocity of the block relative to the frame is

View SolutionA uniform rod of mass m and length l is fixed from Point A, which is at a distance l/4 from one end as shown in the figure. The rod is free to rotate in a vertical plane. The rod is released from the horizontal position.

What is the reaction at the hinge, when kinetic energy of the rod is maximum?
View SolutionThe ends of a rod of length l and mass m are attached to two identical springs as shown in the figure. The rod is free to rotate about its centre O . The rod is depressed slightly at end A and released . The time period of the oscillation is
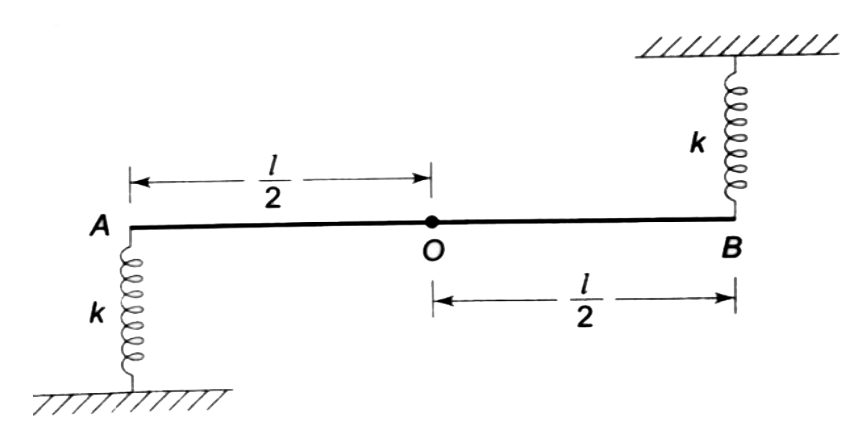
View Solution
A uniform rod AB of mass m and length L rotates about a fixed vertical axis making a constant angle θ with it as shown in figure. The rod is rotated about this axis, so that point B the free end of the rod moves with a uniform speed V in the horizontal plane then the angular momentum of the rod about the axis is:
View Solution
A uniform rod AB of mass m and length L rotates about a fixed vertical axis making a constant angle θ with it as shown in figure. The rod is rotated about this axis, so that point B the free end of the rod moves with a uniform speed V in the horizontal plane then the angular momentum of the rod about the axis is:
View SolutionIf two charged particles each of charge q mass m are connected to the ends of a rigid massless rod and is rotated about an axis passing through the centre and ⊥ to length. Then find the ratio of magnetic moment to angular momentum
View Solution