Two blocks are arranged as in figure Then is friction between ground and only and other surface are frictionless between ground and The maximum ratio of and so that the system remain is at rest

none of these
The correct Answer is:a
AS sphere is at rest
…(i)
…(ii)
and
Here

Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Multiple Correct
2 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Linked Comprehension
52 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Subjective
21 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
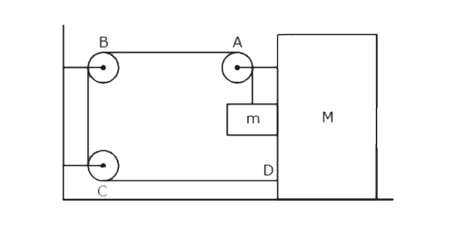
In figure find the acceleration of m assuming that there is friction between mandM and all other surface are smooth and pulleys light and μ=coefficient of friction between mandM

View SolutionWrite equations of forces in terms of the relative acceleration for the blocks shown in and find the relation between m and M so that system remains at rest
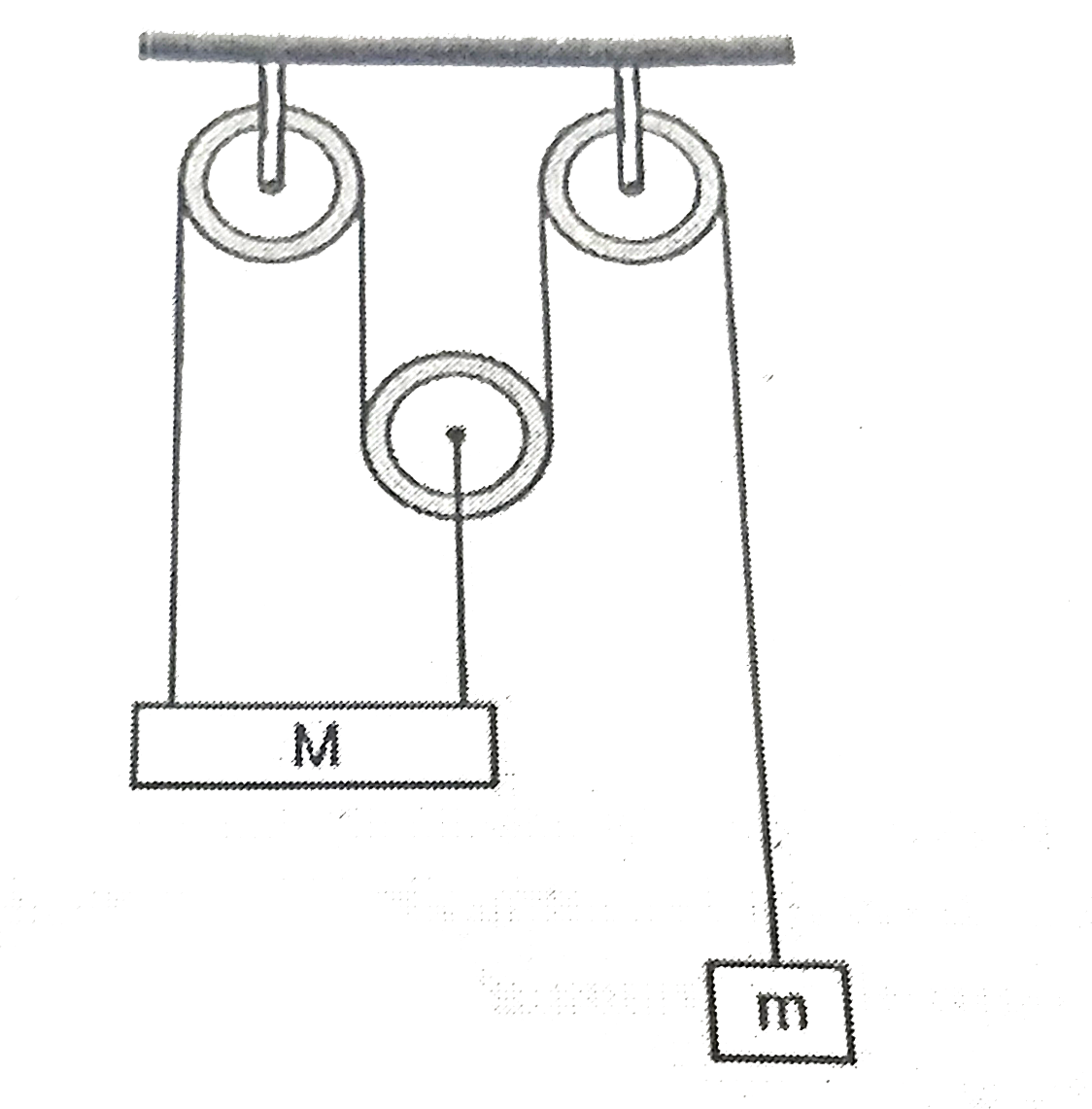
View Solution
Knowledge Check
Two blocks M and m are arranged as shown in the diagram The coefficient of friction between the block is μ1=0.25 and between the ground and M is μ2=13 If M=8kg then find the value of m so that the system will remain at rest
 A4/3kgB8/9kgC1kgD8/5kg
A4/3kgB8/9kgC1kgD8/5kgCalculate angle of friction between wedge and block system is at rest M coefficient of friction between wedge and block.
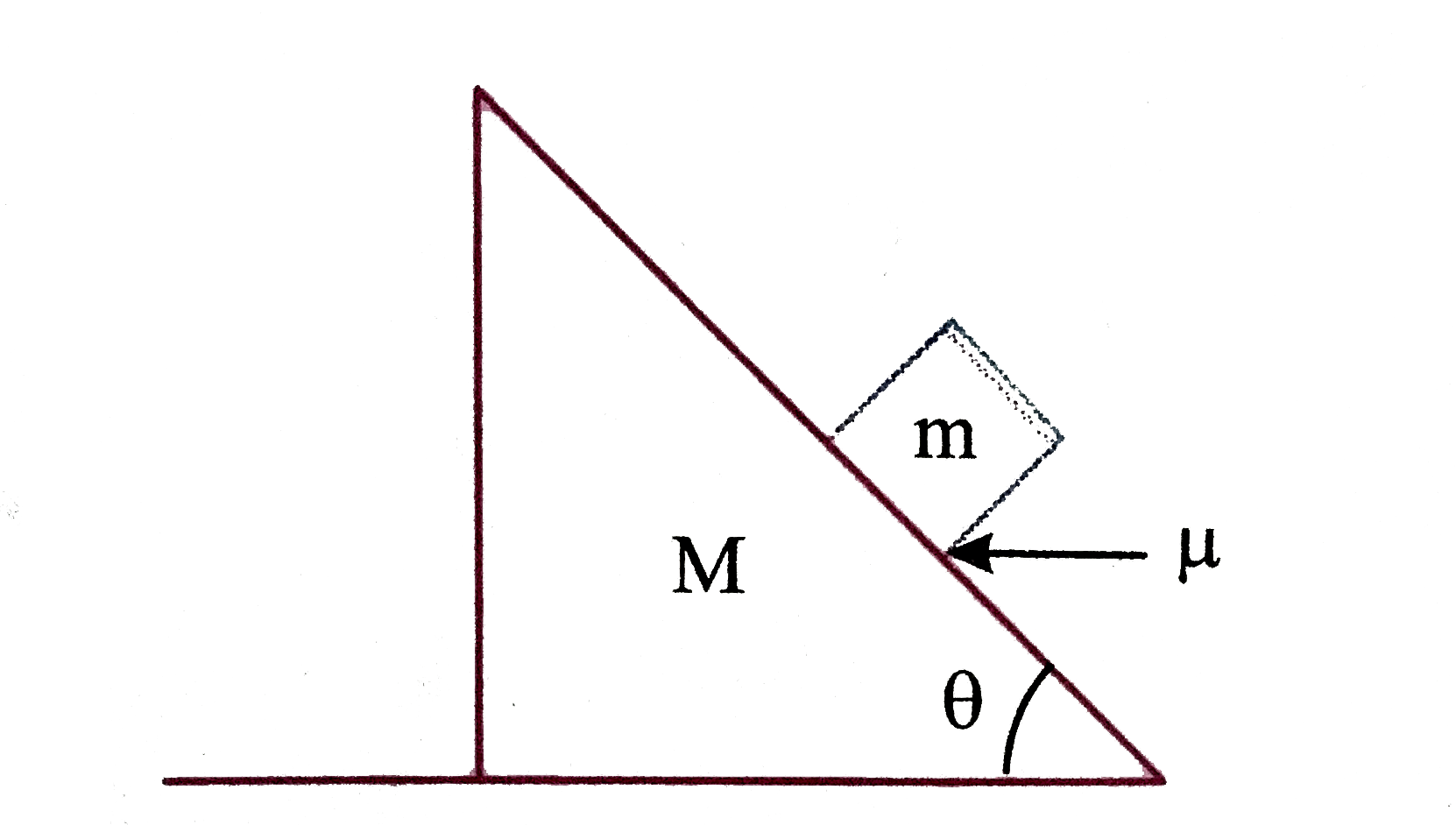 Atan−1μB2θCθDθ2
Atan−1μB2θCθDθ2In Fig. 7.150 , coefficient of friction between m2 and the horizontal surface is μ , minimum value of m so that the system has zero acceleration , is :
 Aμ(m1+m2)Bμ(m1+m2)Cm2−m1μDm1μ−m2
Aμ(m1+m2)Bμ(m1+m2)Cm2−m1μDm1μ−m2
Two blocks of mass 'm' and 'M, are connect to the ends of a string passing over a pulley. 'M' lies on the plane inclined at an angle θ with the horizontal and 'm' is hanging vertically as shown in Fig. The coefficient of static friction between 'M' and the incline is μs. Find the minimum and maximum value of 'm' so that the system is at rest.
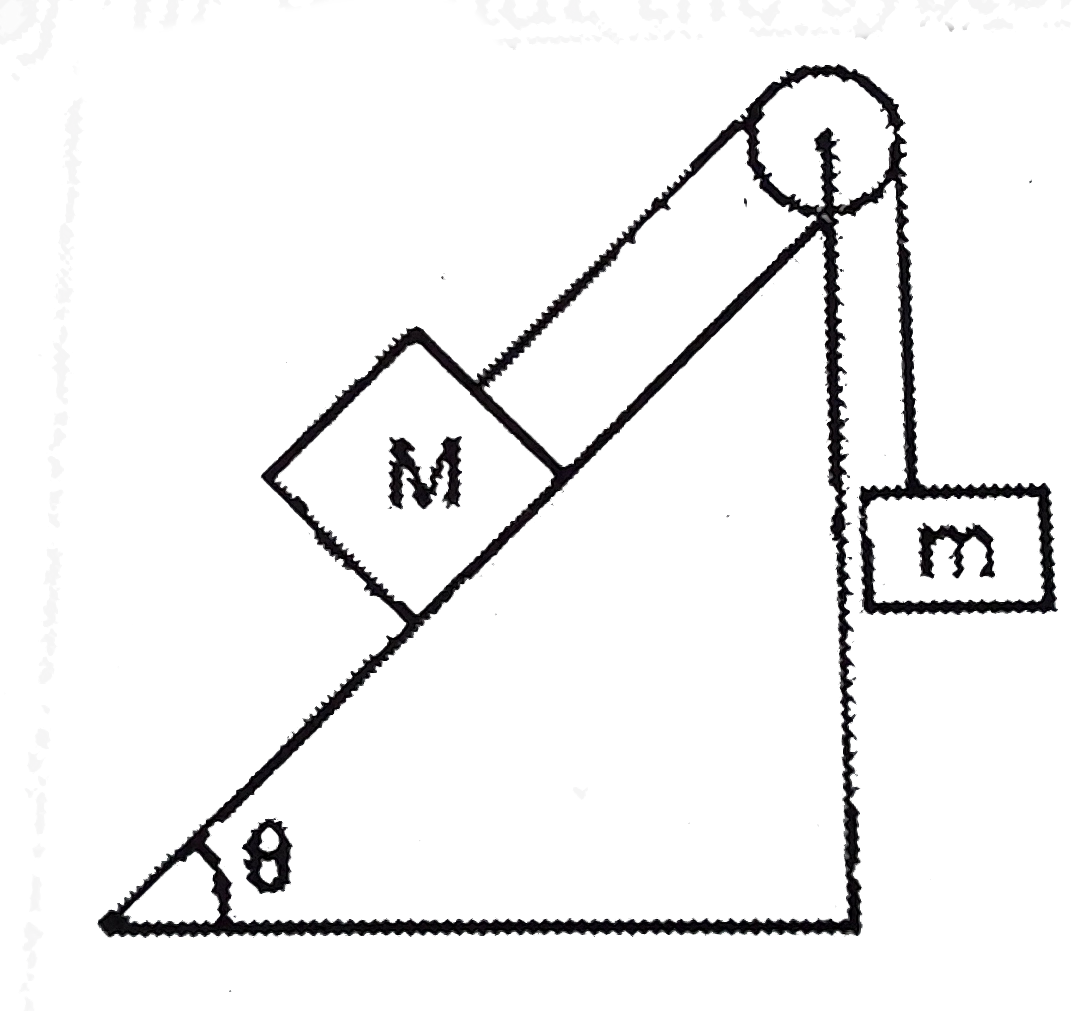
View SolutionIn figure , find the acceleration of m assuming that there is friction between m and M,and all other surface are smooth and pulleys light and m = coeffiicient of friction between m and M .
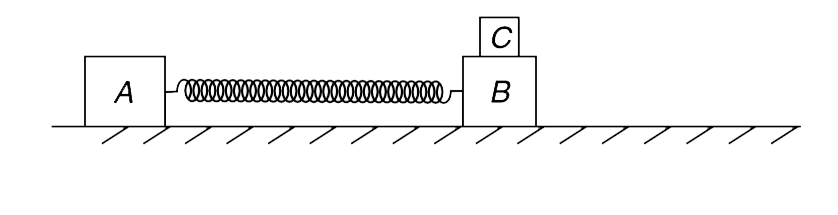
View SolutionTwo block A and B are connected to a spring (force constant k = 480 N/m) and placed on a horizontal surface. Another block C is placed on B. The coefficient of friction between the floor and block A is μ1=0.5, whereas there is no friction between B and the floor. Coefficient of friction between C and B is μ2=0.85. Masses of the blocks are MA=50kg,MB=28 kg and MC=2kg. The system is held at rest with spring compressed by x0=0.5m. After the system is released, find the maximum speed of block B during subsequent motion.
View SolutionA block of mass M is placed on a rough horizontal surface. It is connected by means of a light inextensible string passing over a smooth pulley . The other end of string is connected to a block of mass m. There is no friction between vertical surface and block m
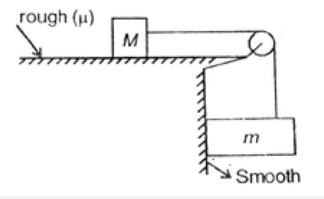
The minimum value of coefficient of friction μ such that system remains at rest , is
View SolutionThe two blocks, m= 10 kg and M = 50 kg are free to move as shown. The coefficient of static friction between the blocks is 0.5 and there is no friction between M and the ground. A minimum horizontal force F is applied to hold m against M that is equal to -

View Solution
