Two blocks of masses m1andm2 are connected by a spring of spring constant k figure. The block of mass m2 is given a shapr imulse so that it acquires a velocity v0 twoards right. Find a. the velocity of the cenre of mas b. the maximum elongation that teh spring will suffer.
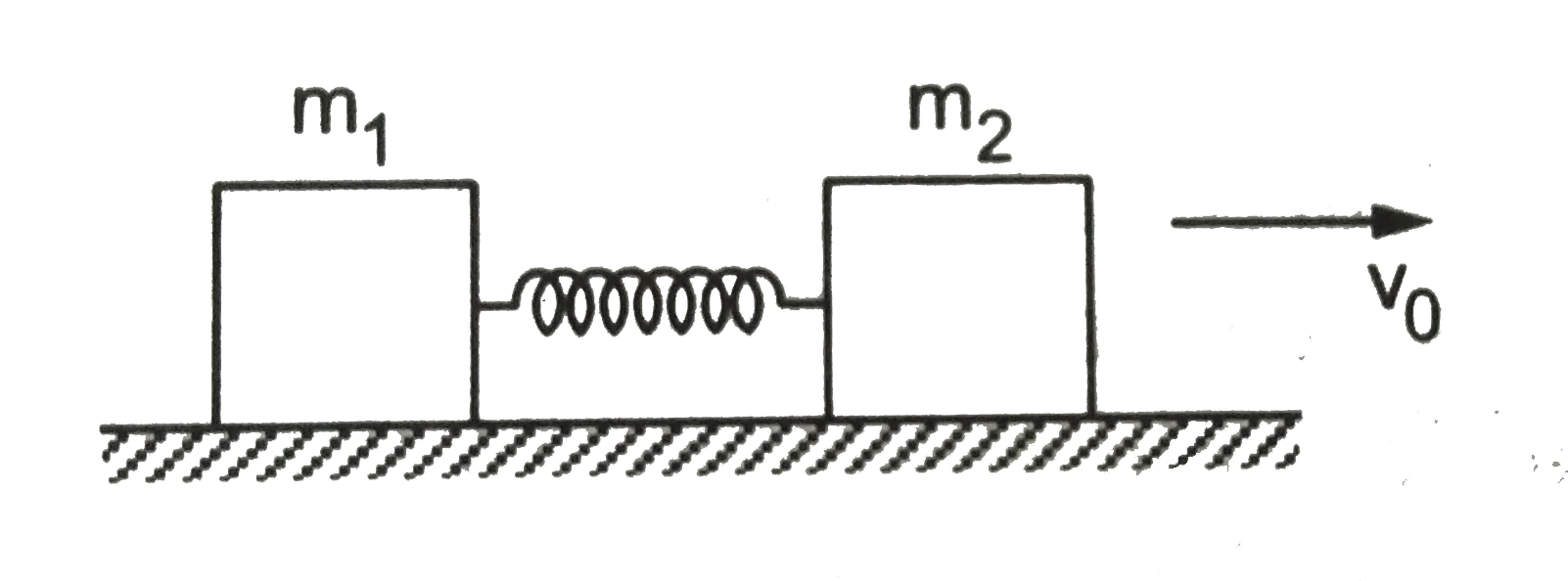
Velocity of centre of mass
=m1v1+m2v2m1+m2
Hence v1=0,v2=v0
=m1×0+m2×v0m1+m−2
=m2v0m1+m2
b. The spring wil attain maximum elongation when both velocities of two blocks wil attain are veolicy of centre of mass.
x→maxiμmelongationofspr∈g<br>chan≥∈k∈etice≠rgy<br>=potentiale≠rgys→red∈spr∈g<br>rarr 1/2 m_2v_2^2-1/2(m_1+m_2)((m_2v_0)/(m_1+m_2))^2<br>=1/2kx^2<br>rarr m_2v_0^2(1-m^2/(m_1+m_2)=kx^2<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/HCV_VOL1_C09_E01_104_S01.pngwh=80%mx-autosty≤=background:white;><br>rarr x=[(m_1m_2)/(m_1+m_2)]^91/2)V_0
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMACHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective 2
11 Videos
- CALORIMETRYBOOK - HC VERMACHAPTER - CALORIMETRYEXERCISE - Exercises
18 Videos
- CIRCULAR MOTIONBOOK - HC VERMACHAPTER - CIRCULAR MOTIONEXERCISE - Exercises
30 Videos
Similar Questions
A block of mass m suspended from a spring of spring constant k. Find the amplitude of S.H.M.
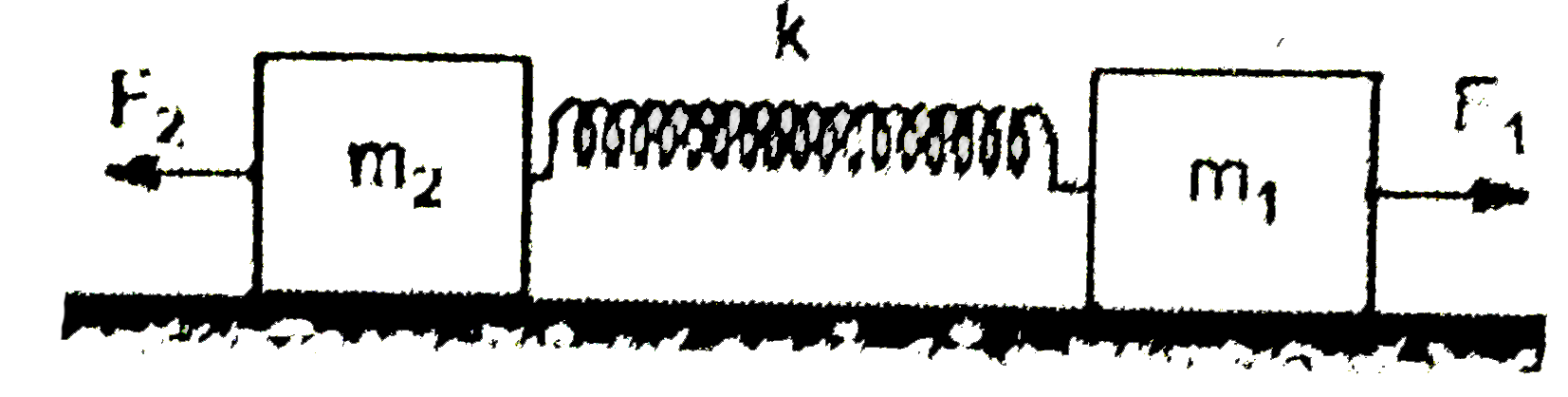
View SolutionTwo blocks of mass m1andm2 are connected by a spring of force constant k. Block of mass m1 os pulled by a constant force f2 [see fig 4E.19 (a)] find the maximum elongation in the spring .
View Solution
Knowledge Check
Two blocks of masses m1=1kg and m2 = 2kg are connected by a spring of spring constant k = 24 N/m and placed on a frictionless horizontal surface. The block m1 is imparted an initial velocity v0 = 12cm/s to the right. The amplitude of osciallation is
A2 cmB1 cmC3 cmD4 cmTwo blocks of masses m1 and m2 are connected by an ideal sprit, of force constant k. The blocks are placed on smooth horizontal surface. A horizontal force F acts on the block m1. Initially spring is relaxed, both the blocks are at rest.
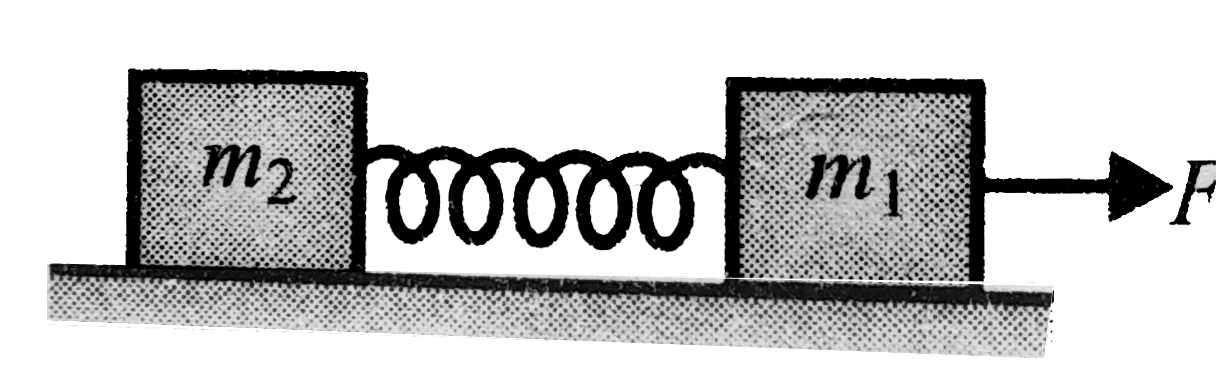
What is maximum elongation of spring.A2m1F(m1+m2)kBm21F2(m1+m2)kC2m2Fk(m1+m2)Dm22F2(m1+m2)2kTwo block A and B of masses m and 2m respectively are connected by a spring of spring cosntant k. The masses are moving to the right with a uniform velocity v0 each, the heavier mass leading the lighter one. The spring is of natural length during this motion. Block B collides head on with a thrid block C of mass 2m. at rest, the collision being completely inelastic.
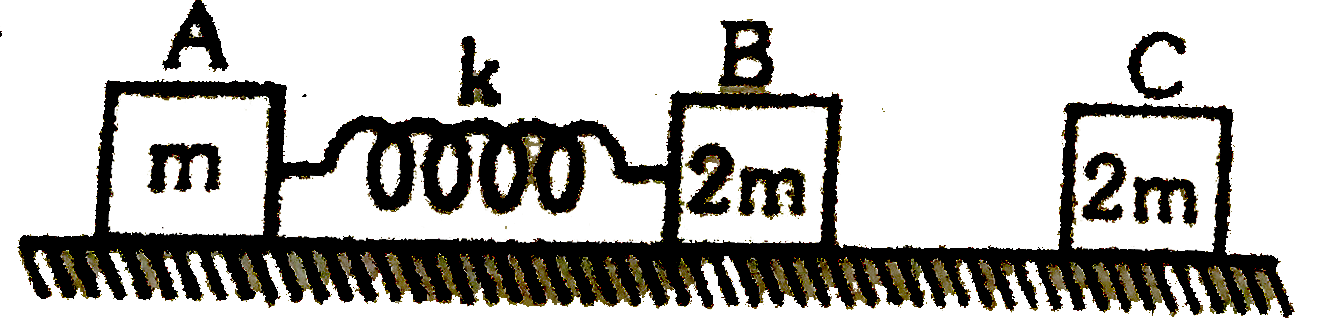
The velocity of centre of mass of system of block A, B, & C is -Av0B3v05C2v05Dv02
Two blocks A and B of mass m and 2m respectively are connected by a massless spring of spring constant K. This system lies over a smooth horizontal surface. At t=0 the bolck A has velocity u towards right as shown while the speed of block B is zero, and the length of spring is equal to its natural length at that at that instant.

Column IColumn II(A)The velocity of block A(P)can never be zero(B)The velocity of block B(Q)may be zero at certain instants of time(C)The kinetic energy of system of two block(R)is minimum at maximum compression of spring(D)The potential energy of spring(S)is maximum at maximum extension of spring
View SolutionBlock of mass 2m is given v0 towards the right. If L is the natural length of spring constant k, find the maximum elongation of the spring.

View SolutionTwo block A and B of masses m and 2m respectively are connected by a spring of spring cosntant k. The masses are moving to the right with a uniform velocity v0 each, the heavier mass leading the lighter one. The spring is of natural length during this motion. Block B collides head on with a thrid block C of mass 2m. at rest, the collision being completely inelastic.
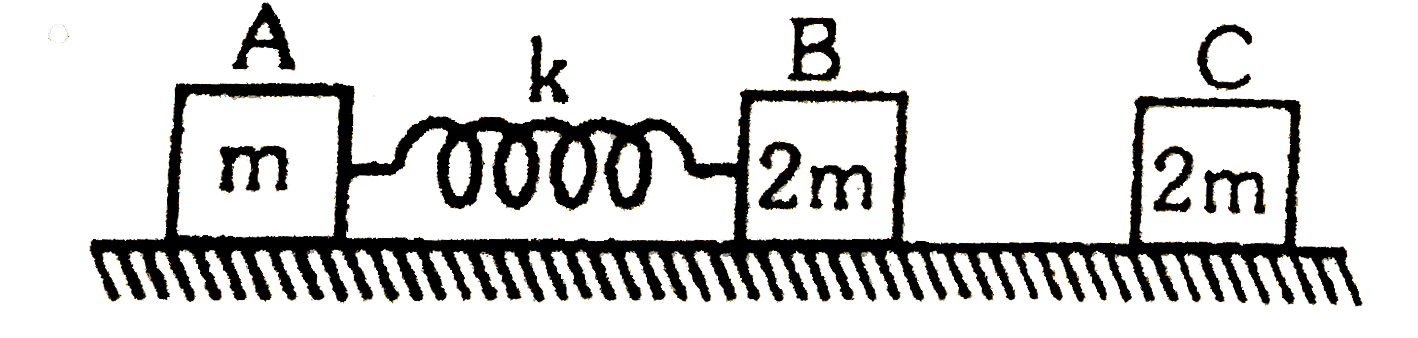
The maximum compression of the spring after collision is -
View SolutionTwo block A and B of masses m and 2m respectively are connected by a spring of spring cosntant k. The masses are moving to the right with a uniform velocity v0 each, the heavier mass leading the lighter one. The spring is of natural length during this motion. Block B collides head on with a thrid block C of mass 2m. at rest, the collision being completely inelastic.
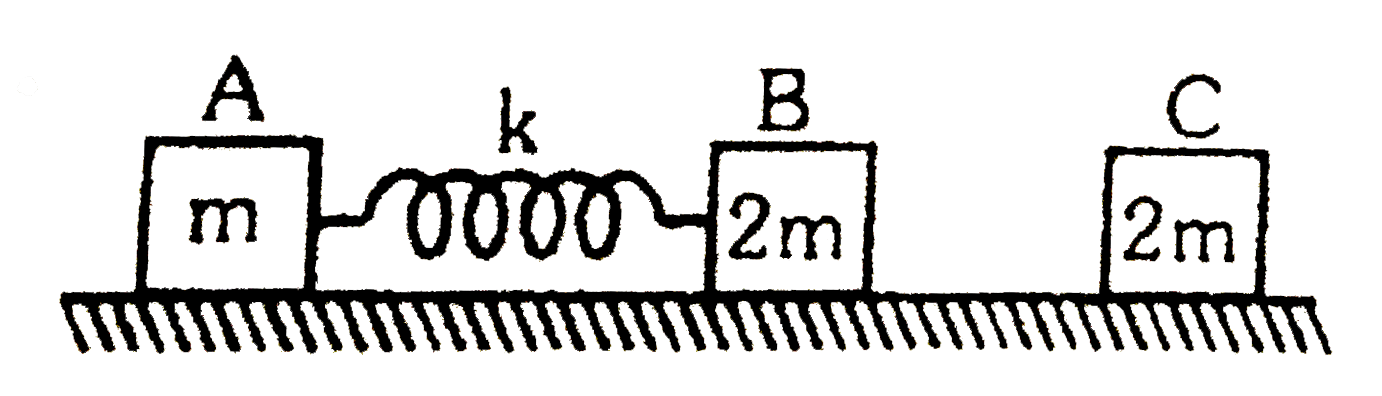
The velocity of block B just after collision is -
View SolutionTwo blocks of masses m1 and m2 are connected by a spring having spring constant K. Initially , the spring is at its natural length. The coefficient of friction between the blocks and the surface is μ. What minimum constant force has to be applied in the horizontal direction to the block of mass m1, in order to shift the other block ?
View Solution
