Two bodies of masses 4 kg and 16 kg at rest to acted upon by same force. The ratio of times required to attain the same speed is,
1:1
4:1
1:4
1:2
The correct Answer is:C
To solve the problem, we need to find the ratio of times required for two bodies of different masses to attain the same speed when acted upon by the same force. Let's break down the solution step by step.
Step 1: Identify the masses and the force
Let:
- Mass of the first body, m1=4kg
- Mass of the second body, m2=16kg
- Force applied, F (same for both bodies)
Step 2: Calculate the acceleration for each body
Using Newton's second law, the acceleration a can be calculated as:
a=Fm
For the first body:
a1=Fm1=F4
For the second body:
a2=Fm2=F16
Step 3: Use the kinematic equation to find time
Since both bodies start from rest, we can use the equation:
v=u+at
where u=0 (initial velocity), v is the final velocity, and t is the time taken.
For the first body:
v=0+a1t1⟹v=F4t1⟹t1=4vF
For the second body:
v=0+a2t2⟹v=F16t2⟹t2=16vF
Step 4: Find the ratio of times
Now, we need to find the ratio t1t2:
t1t2=4vF16vF=4vF⋅F16v=416=14
Conclusion
The ratio of times required to attain the same speed is:
t1t2=1:4
Let:
- Mass of the first body, m1=4kg
- Mass of the second body, m2=16kg
- Force applied, F (same for both bodies)
Using Newton's second law, the acceleration a can be calculated as:
a=Fm
For the first body:
a1=Fm1=F4
For the second body:
a2=Fm2=F16
Since both bodies start from rest, we can use the equation:
v=u+at
where u=0 (initial velocity), v is the final velocity, and t is the time taken.
v=0+a1t1⟹v=F4t1⟹t1=4vF
v=0+a2t2⟹v=F16t2⟹t2=16vF
Now, we need to find the ratio t1t2:
t1t2=4vF16vF=4vF⋅F16v=416=14
The ratio of times required to attain the same speed is:
t1t2=1:4
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE - II
136 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
10 Videos
- LOGIC GATESBOOK - AAKASH SERIESCHAPTER - LOGIC GATESEXERCISE - Exercise (Very Short Answer)
10 Videos
Similar Questions
Two bodies of masses 4 kg and 5kg are acted upon by the same force. If the acceleration of lighter body is 2m/sec2, then the acceleration of the heavier body is:-
View SolutionTwo bodies of masses 1 kg and 2 kg moving with same velocities are stopped by the same force. Then, the ratio of their stopping distances is
View Solution
Knowledge Check
Two bodies A and B have masses 20 kg and 5 kg respectively. Each one is acted upon by a force of 4 kg wt. If they acquire the same kinetic energy in times tA and tB, then the ratio tAtB is
A12B2C25D56
Two bodies of mass 1kgand2kg have equal momentum. The ratio of their kinetic energies is:
View SolutionTwo bodies of masses 4 kg and 5 kg are moving with equal momentum. Then the ratio of their respective kinetic energies is
View SolutionIf a body of mass 5 kg initially at rest is acted upon by a force of 50 dyne for 3s, then the impulse will be
View SolutionA block of mass m at rest is acted upon by a force F for a time t. The kinetic energy of block after time t is
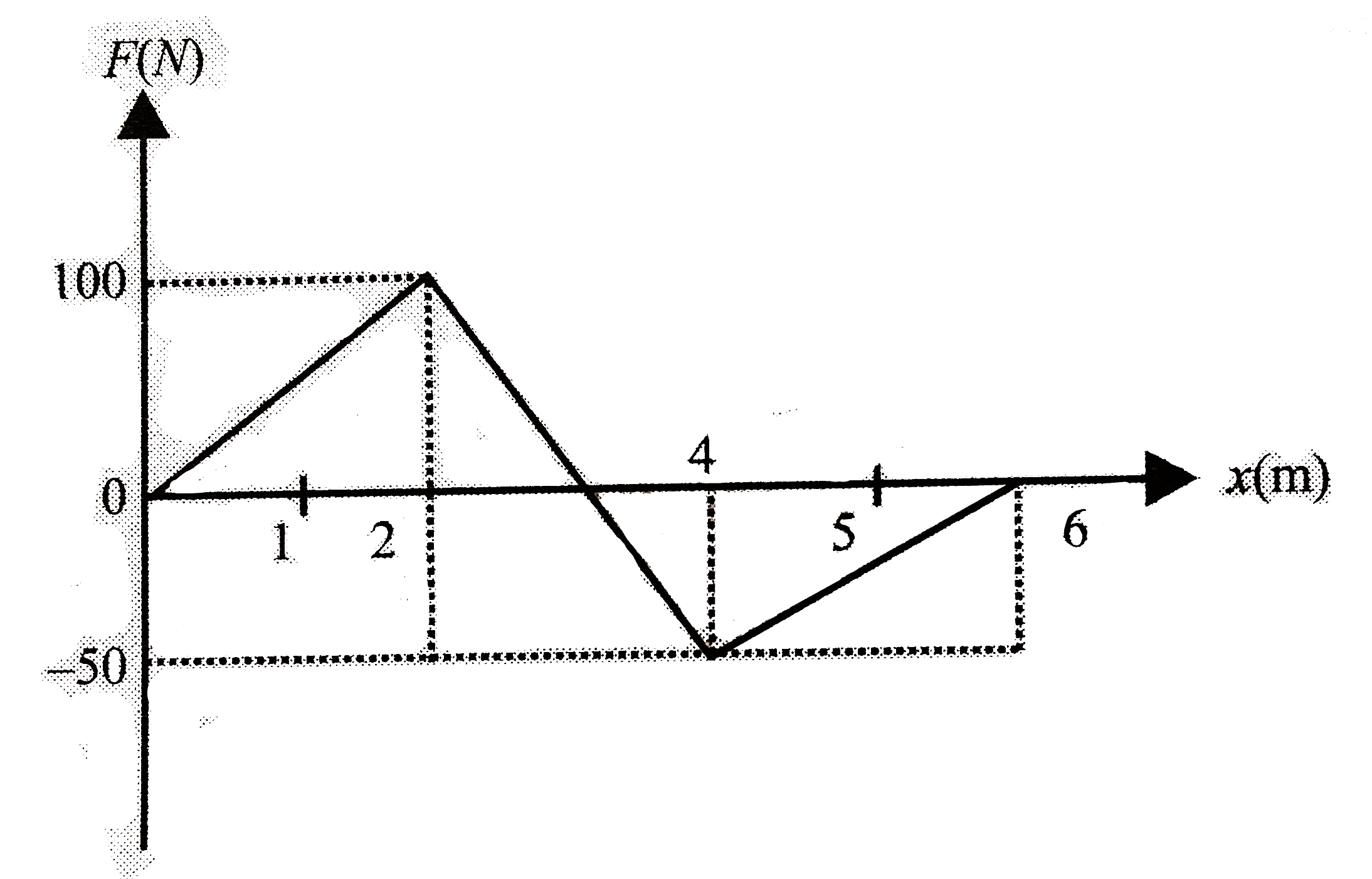
View SolutionA stationary particle of mass m=1.5kg is acted upon by a variable force. The variation of force with respect to displacement is plotted in figure.
a. Calculate the velocity acquired by the particle after getting displaced through 6m.
b. What is the maximum speed attained by the particle and at what time is it attained?
View SolutionA body of mass 500 g, initially at rest, is acted upon by a force which causes it to move a distance of 4 m in 2 s, Calculate the force applied.
View SolutionTwo masses of 1 kg and 16 kg are moving with equal kinetic energy. The ratio of magnitude of the linear momentum is:
View Solution
