A balloon of total mass 1000 Kg float motionless over the earth's surface. If 100 kg of sand ballast are thrown over board, the balloon starts to rise with an acceleration of
10m/s2
9.8m/s2
1.09m/s2
4.9m/s2
The correct Answer is:C
To solve the problem, we will use Newton's second law of motion and the concept of buoyancy.
1. Identify the Initial Conditions:
- The total mass of the balloon when it is floating motionless is minitial=1000kg.
- The weight of the balloon is given by Winitial=minitial⋅g=1000kg⋅9.8m/s2=9800N.
2. Determine the Buoyant Force:
- Since the balloon is floating motionless, the buoyant force Fb acting on it is equal to its weight:
Fb=Winitial=9800N
3. Calculate the New Mass After Throwing Sand:
- When 100 kg of sand is thrown overboard, the new mass of the balloon becomes:
mfinal=1000kg−100kg=900kg
4. Calculate the Weight of the Balloon After Throwing Sand:
- The new weight of the balloon is:
Wfinal=mfinal⋅g=900kg⋅9.8m/s2=8820N
5. Determine the Net Force Acting on the Balloon:
- The net force Fnet acting on the balloon when the sand is thrown is given by the difference between the buoyant force and the new weight:
Fnet=Fb−Wfinal=9800N−8820N=980N
6. Apply Newton's Second Law to Find Acceleration:
- According to Newton's second law, Fnet=mfinal⋅a, where a is the acceleration of the balloon:
980N=900kg⋅a
- Solving for a:
a=980N900kg≈1.09m/s2
Final Answer:
The balloon starts to rise with an acceleration of approximately 1.09m/s2.
- The total mass of the balloon when it is floating motionless is minitial=1000kg.
- The weight of the balloon is given by Winitial=minitial⋅g=1000kg⋅9.8m/s2=9800N.
- Since the balloon is floating motionless, the buoyant force Fb acting on it is equal to its weight:
Fb=Winitial=9800N
- When 100 kg of sand is thrown overboard, the new mass of the balloon becomes:
mfinal=1000kg−100kg=900kg
- The new weight of the balloon is:
Wfinal=mfinal⋅g=900kg⋅9.8m/s2=8820N
- The net force Fnet acting on the balloon when the sand is thrown is given by the difference between the buoyant force and the new weight:
Fnet=Fb−Wfinal=9800N−8820N=980N
- According to Newton's second law, Fnet=mfinal⋅a, where a is the acceleration of the balloon:
980N=900kg⋅a
- Solving for a:
a=980N900kg≈1.09m/s2
The balloon starts to rise with an acceleration of approximately 1.09m/s2.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE - II
136 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
10 Videos
- LOGIC GATESBOOK - AAKASH SERIESCHAPTER - LOGIC GATESEXERCISE - Exercise (Very Short Answer)
10 Videos
Similar Questions
The force of buoyancy exerted by the atmosphere on a balloon is B in the upward direction and remains constant. The force of air resistance on the balloon acts opposite to the direction of velocity and is proportional to it. The balloon carries a mass M and is found to fall down near the earth's surface with a constant velocity v. How uch mass hsould be removed from teh balloon so that it may rise with a constant velocity v?
View SolutionA balloons of mass M is descending at a constant acceleration α. When a mass m is released from the balloon, it starts rising. With the same acceleration α. Assuming that its volumes does not change, what is the valule of m?
View SolutionA balloons of mass M is descending at a constant acceleration α. When a mass m is released from the balloon, it starts rising. With the same acceleration α. Assuming that its volumes does not change, what is the valule of m?
View SolutionA balloon starts rising from the earth's surface. The ascension rate is constant and equal to v0. Due to the wind. The balloon gathers the horizontal velocity component vx=ky, where k is a constnat and y is the height of ascent. Find how the following quantities depednd on the height of ascent.
(a) the horizontal drift of the balloon x (y)
(b) the total tangential and normal accelrations of the balloon.
View SolutionIn order to raise a mass of 100 kg, a man of mass 60 kg fastens a rope to it and passes the rope over a smooth pulley. He climbs the rope with acceleration 5g/4 relative to the rope. The tension in the rope is (take g=10ms−2)

View SolutionTwo men to masses 80kg and 60kg are standing on a wood plank of mass 100kg, that has been placed over a smooth surface. If both the men start moving towards each other with speeds 1m/s and 2m/s respectively then find the velocity of the plank by which it starts moving.
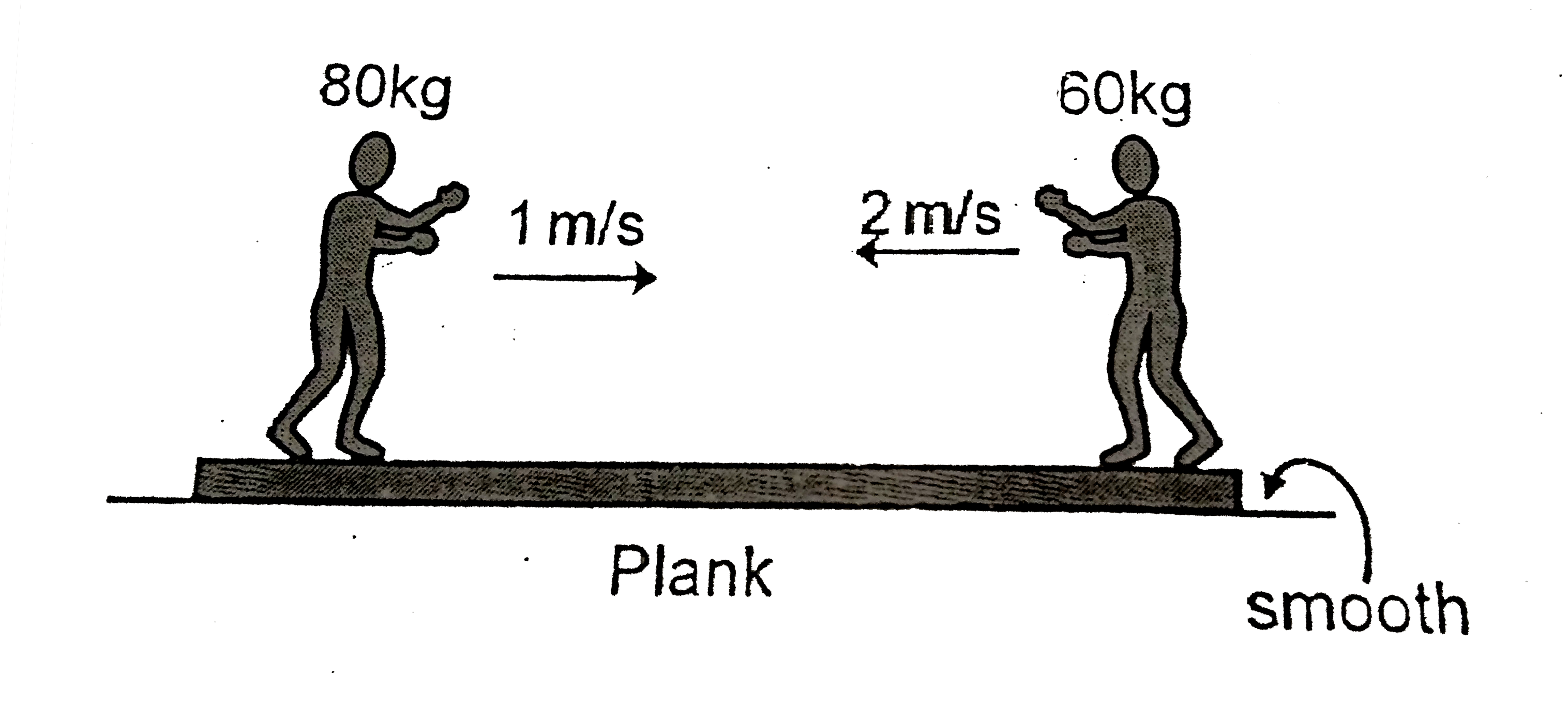
View SolutionA block of mass 10 kg is kept over a rough surface and a force F=4t is applied on it. At what value of t the block will start moving :-
View SolutionA cart of mass 150 kg is pulled horizontally on a frictionless surface with face 10 N. If 100 g/s sand is being dropped in the cart verticlly then find the speed of the system when cart has 100 kg snad in it.
View SolutionA 2 kg mass placed on a level table and is attached by a string passing over the edge of a table as illustrated in the diagram.
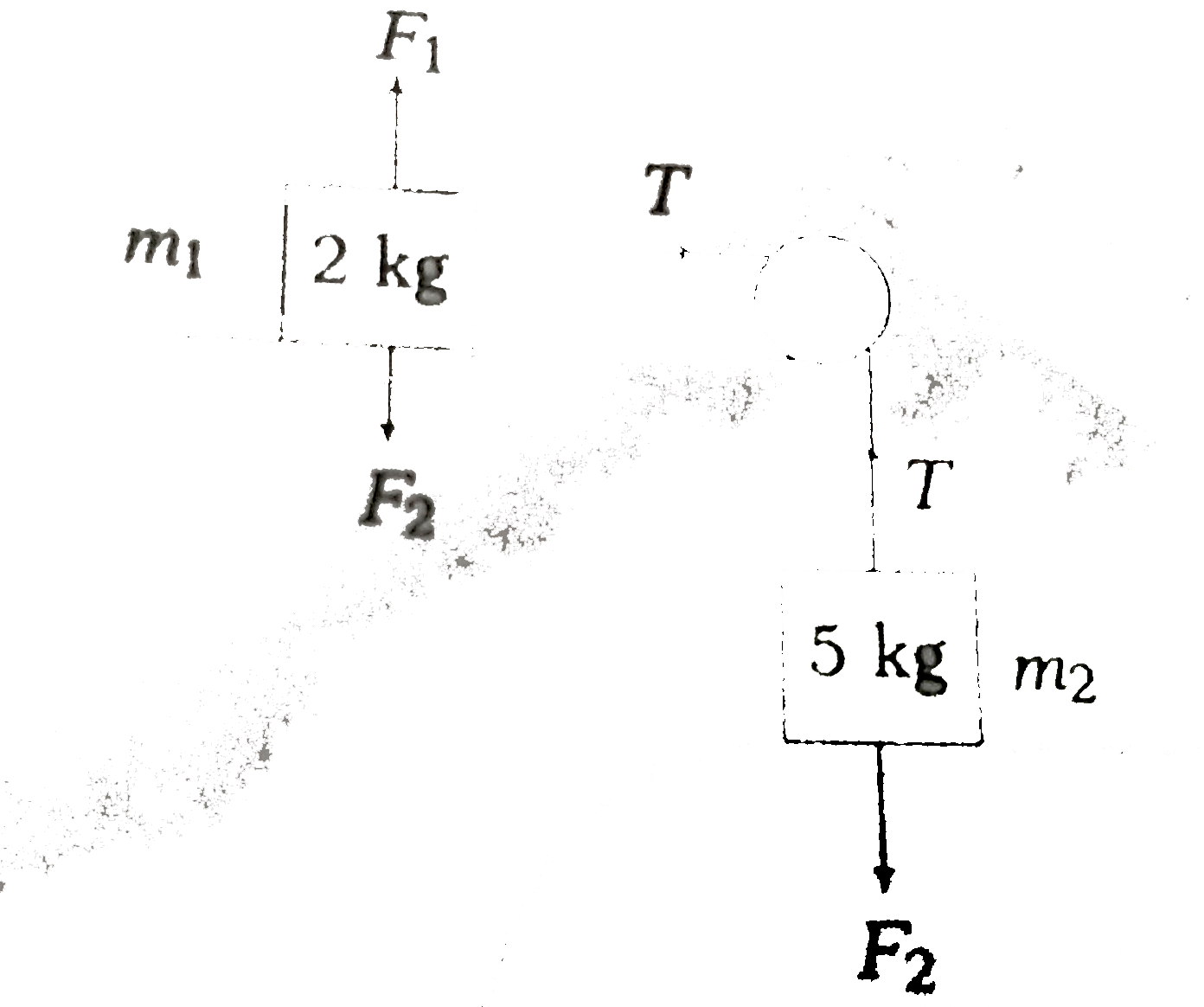
(i) Calculate the magnitude of acceleration of the system.
(ii) Calculate the tension in the string.
View SolutionA constant force F is applied on a trolley of initial mass m0 kept over a smooth surface. Sand is poured gently over the trolley at a constant rate of (μ)kg//s. Afer time t, find

(a) mass of the trolley (with sand)
(b) net force on the trolley
(c) velocity of trolley
View Solution
