Two bodies of masses m1 and m2(m1>m2) respectively are tied to the ends j of a string which passes over a light frictionless pulley. The masses are intitially at rest and released. What is the acceleration of the centre of mass ?
The correct Answer is:a=(m1−m2)2g(m1+m2)2
To find the acceleration of the center of mass of the two-body system connected by a string over a pulley, we can follow these steps:
Step 1: Identify the forces acting on the masses
- For mass m1 (which is greater than m2), the forces acting are:
- Weight: m1g (downward)
- Tension: T (upward)
- For mass m2:
- Weight: m2g (downward)
- Tension: T (upward)
Step 2: Write the equations of motion
- For mass m1:
m1g−T=m1a
(Equation 1)
- For mass m2:
T−m2g=m2a
(Equation 2)
Step 3: Solve the equations simultaneously
- From Equation 1, we can express T:
T=m1g−m1a
- Substitute T in Equation 2:
(m1g−m1a)−m2g=m2a
Simplifying this gives:
m1g−m1a−m2g=m2a
Rearranging terms:
m1g−m2g=m1a+m2a
(m1−m2)g=(m1+m2)a
Step 4: Solve for acceleration a
- From the above equation, we can solve for a:
a=(m1−m2)gm1+m2
Step 5: Find the acceleration of the center of mass
- The acceleration of the center of mass acm for a two-body system is given by the formula:
acm=m2m1+m2g
Final Result
Thus, the acceleration of the center of mass is:
acm=m2m1+m2g
---
- For mass m1 (which is greater than m2), the forces acting are:
- Weight: m1g (downward)
- Tension: T (upward)
- Weight: m2g (downward)
- Tension: T (upward)
- For mass m1:
m1g−T=m1a
(Equation 1)
T−m2g=m2a
(Equation 2)
- From Equation 1, we can express T:
T=m1g−m1a
(m1g−m1a)−m2g=m2a
Simplifying this gives:
m1g−m1a−m2g=m2a
Rearranging terms:
m1g−m2g=m1a+m2a
(m1−m2)g=(m1+m2)a
- From the above equation, we can solve for a:
a=(m1−m2)gm1+m2
- The acceleration of the center of mass acm for a two-body system is given by the formula:
acm=m2m1+m2g
Thus, the acceleration of the center of mass is:
acm=m2m1+m2g
Topper's Solved these Questions
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 2 (FROM MOMENT OF INERTIA, TORQUE)
22 Videos
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 2 (FROM ANGULAR MOMENTUM - CONSERVATION)
14 Videos
- CIRCULAR MOTION BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 2 (FROM EQUATIONS OF ROTATIONAL MOTION)
8 Videos
- COMPETITION CARE UNITBOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - OBJECTIVE QUESTIONS FROM PREVIOUS IAS EXAMINATIONS
50 Videos
Similar Questions
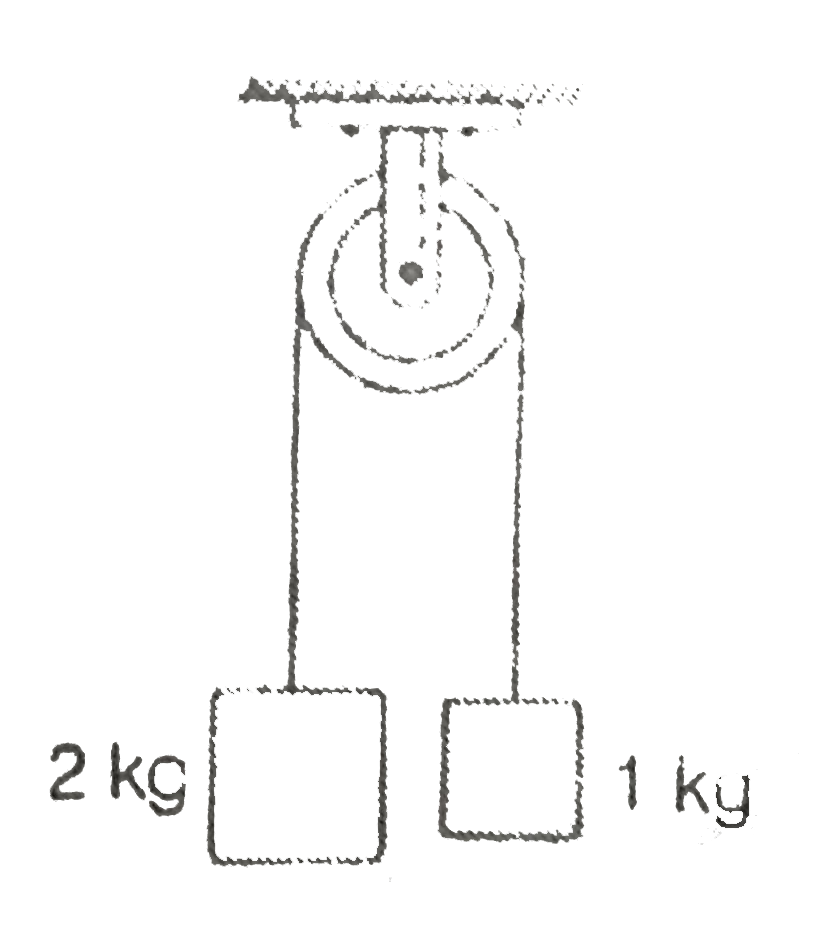
Two blocks of masses 2 kg and 1 kg respectively are tied to the ends of a string which passes over a light frictionless pulley . The masses are held at rest at the same horizontal level and then released . The distance traversed by centre of mass in 2 s is ( g = 10 m/s2)
View SolutionTwo blocks of masses m1=4kg and m2=2kg are connected to the ends of a string which passes over a massless, frictionless pulley. The total downwards thrust on the pulley is nearly

View SolutionTwo bodies of masses 4 kg and 6 kg are tied to the ends of a massless string. The string passes over a frictionless pulley. The acceleration of the system is :
View SolutionTwo blocks of masses m1andm2(m1>m2) connected by a massless string passing over a frictionless pulley Magnitude of acceleration of blocks would be
View SolutionTwo masses M1 and M2 are attached to the ends of a string which passes over a pulley attached to the top of an inclined plane. The angle of inclination of the plane is 30∘ and M1=10kg,M2=5kg. What is the acceleration of mass M2 ?

View SolutionTwo masses 2 kg and 4 kg are connected at the two ends of light inextensible string passing over a frictionless pulley. If the masses are released, then find the acceleration of the masses and the tension in the string.
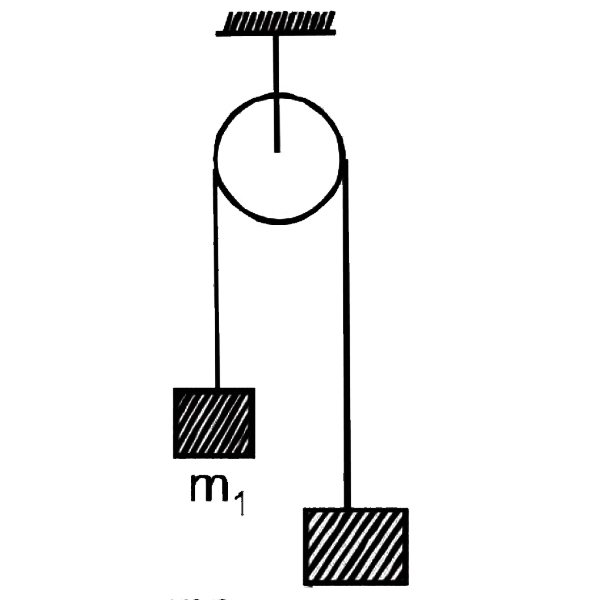
View SolutionTwo masses m1=5kg and m2=4.8kg tied to a string are hanging over a light frictionless pulley. What is the acceleration of the masses when left free to move?
View SolutionTwo particles of masses m and M(M>m) are connected by a cord that passes over a massless, frictionless pulley. The tension T in the string and the acceleration a of the particles is
View SolutionTwo masses 2 kg and 4 kg are connected at two ends of light inextensible string passing over a frictionless pulley . If the masses are released , then find the accelaration of the masses and the tension in the string .
View SolutionTwo bodies of masses m1 and m2 are connected a light string which passes over a frictionless massless pulley. If the pulley is moving upward with uniform acceleration g2, then tension in the string will be
View Solution
