Two capacitors having capacitances C1 and C2 are charged with 120 V and 200 V batteries respectively. When they are connected in parallel now, it is found that the potential on each one of them is zero. Then,
5C1=3C2
8C1=5C2
9C1=5C2
3C1=5C2
The correct Answer is:D
To solve the problem step-by-step, we will analyze the situation involving the two capacitors charged with different voltages and then connected in parallel.
Step 1: Understand the Initial Charges on the Capacitors
When the capacitors are charged with their respective batteries, the charge on each capacitor can be calculated using the formula:
Q=C×V
For Capacitor 1 (C1) charged with 120 V:
Q1=C1×120
For Capacitor 2 (C2) charged with 200 V:
Q2=C2×200
Step 2: Analyze the Connection in Parallel
When the two capacitors are connected in parallel, they are connected such that the positive terminal of one is connected to the negative terminal of the other. This results in the charges on the capacitors opposing each other.
Step 3: Set Up the Equation for Zero Potential
Since it is given that the potential on each capacitor is zero after they are connected in parallel, this implies that the net charge on the system is zero. Therefore, the charges must be equal in magnitude but opposite in sign:
Q1−Q2=0
This means:
Q1=Q2
Step 4: Substitute the Charges
Substituting the expressions for Q1 and Q2:
C1×120=C2×200
Step 5: Rearranging the Equation
Rearranging the equation gives us:
120C1=200C2
Dividing both sides by 40, we simplify this to:
3C1=5C2
Step 6: Final Relation
Thus, we have established the relationship between the capacitances:
3C1=5C2
Conclusion
The final relationship between the capacitances of the two capacitors is:
3C1=5C2
When the capacitors are charged with their respective batteries, the charge on each capacitor can be calculated using the formula:
Q=C×V
For Capacitor 1 (C1) charged with 120 V:
Q1=C1×120
For Capacitor 2 (C2) charged with 200 V:
Q2=C2×200
When the two capacitors are connected in parallel, they are connected such that the positive terminal of one is connected to the negative terminal of the other. This results in the charges on the capacitors opposing each other.
Since it is given that the potential on each capacitor is zero after they are connected in parallel, this implies that the net charge on the system is zero. Therefore, the charges must be equal in magnitude but opposite in sign:
Q1−Q2=0
This means:
Q1=Q2
Substituting the expressions for Q1 and Q2:
C1×120=C2×200
Rearranging the equation gives us:
120C1=200C2
Dividing both sides by 40, we simplify this to:
3C1=5C2
Thus, we have established the relationship between the capacitances:
3C1=5C2
The final relationship between the capacitances of the two capacitors is:
3C1=5C2
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (B) Chapter exercises
17 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
Two capacitors with capacities C1 and C2 ,are charged to potentials V1 and V2 respectively.When they are connected in parallel,the ratio of their respective charges is ....?
View SolutionTwo capacitors C1 and C2 are charged to 120V and 200V respectively. It is found that connecting them together the potential on each one can be made zero. Then
View SolutionTwo capacitors with capacitances C1andC2 are connected in parallel. Find the resultant capacitance.
View SolutionTwo capacitors of 10pF and 20pF are connected to 200 V and 100 V sources, respectively. If they are connected by the wire, then what is the common potential of the capacitors?
View SolutionTwo capacitors of capacitance 2μF and 3μF respectively are charged to potential difference 20 V and 40 V respectively. Now the capacitors are connected in series with a resistance such that the positively charged plate of one capacitor is connected to the positively charged plate of the other. The initial current through the resistance is I0. The potential difference across the 2μF capacitor at the instant the current has reduced to I02 is_______ V.
View SolutionTwo capacitors of capacitance C and 3C are charged to potential difference V0 and 2V0, respectively, and connected to an inductor of inductance L as shows in Fig. Initially, the current in the inductor is zero. Now, switch S is closed.
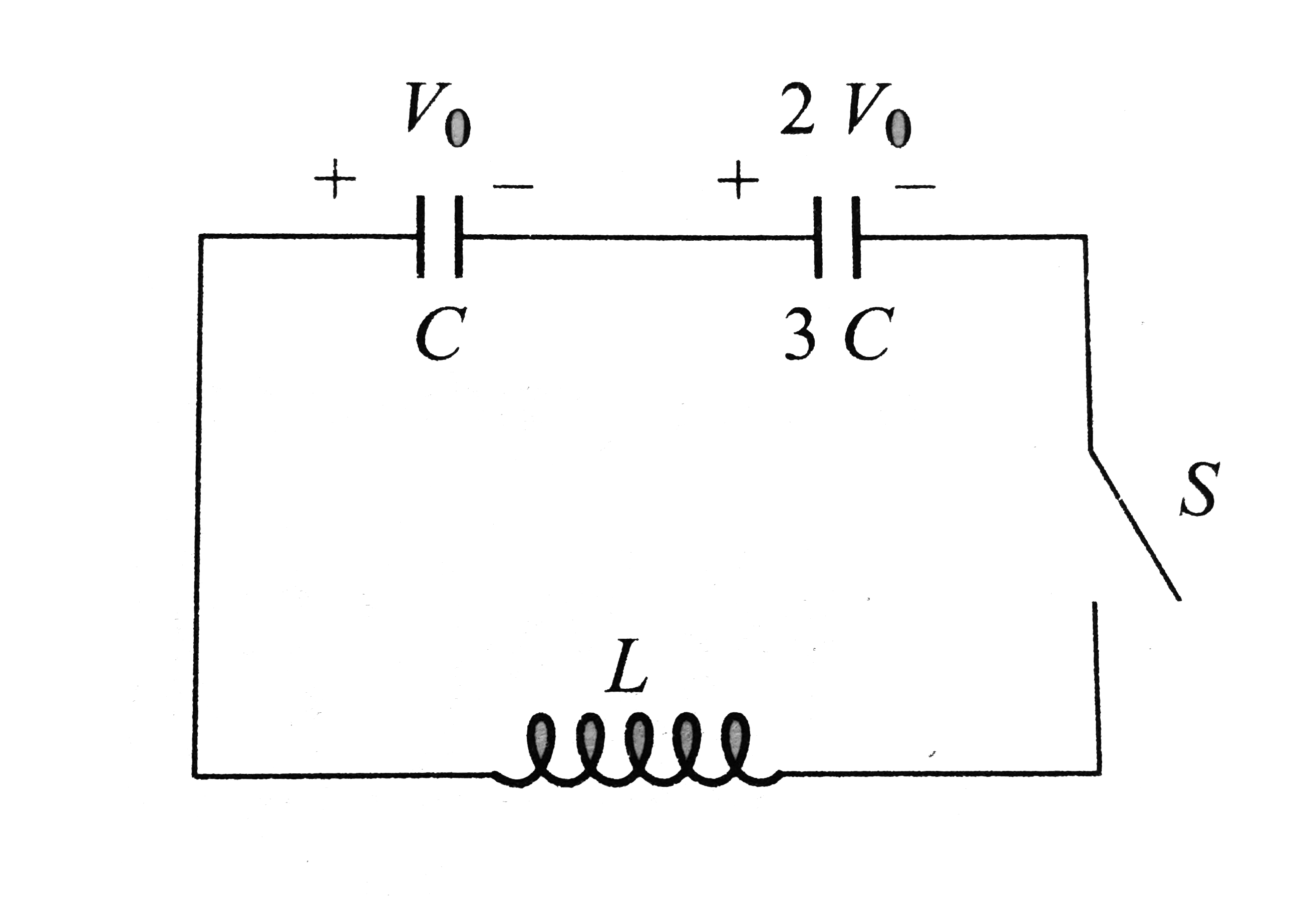
Potential difference across capacitor of capacitance 3C when the current in the circuit is maximum is
View SolutionTwo capacitors of capacitance C and 3C are charged to potential difference V0 and 2V0, respectively, and connected to an inductor of inductance L as shows in Fig. Initially, the current in the inductor is zero. Now, switch S is closed.
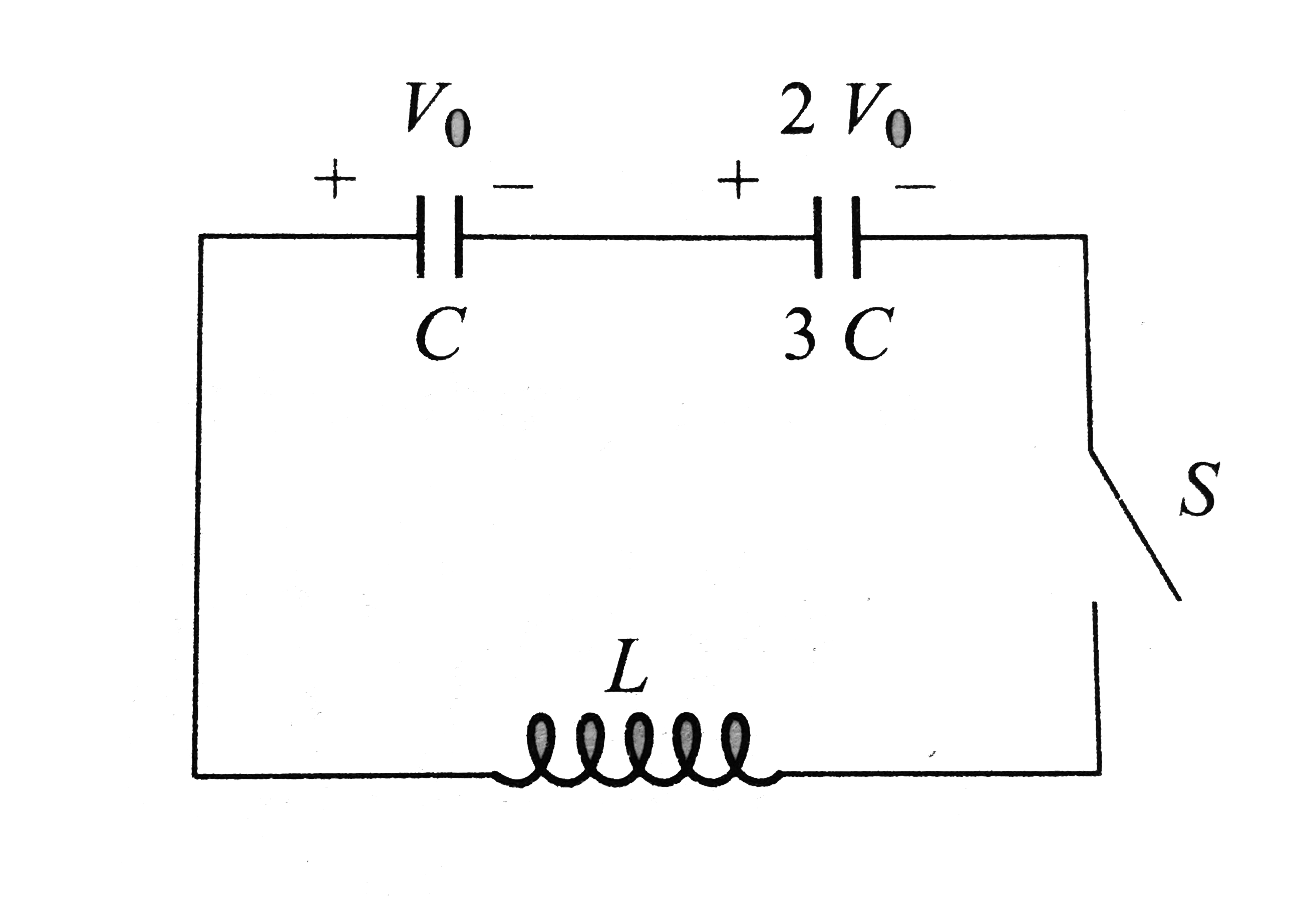
Potential difference across capacitor of capacitance C when the current in the circuit is maximum is
View SolutionTwo capacitors of capacitance C and 3C are charged to potential difference V0 and 2V0, respectively, and connected to an inductor of inductance L as shows in Fig. Initially, the current in the inductor is zero. Now, switch S is closed.
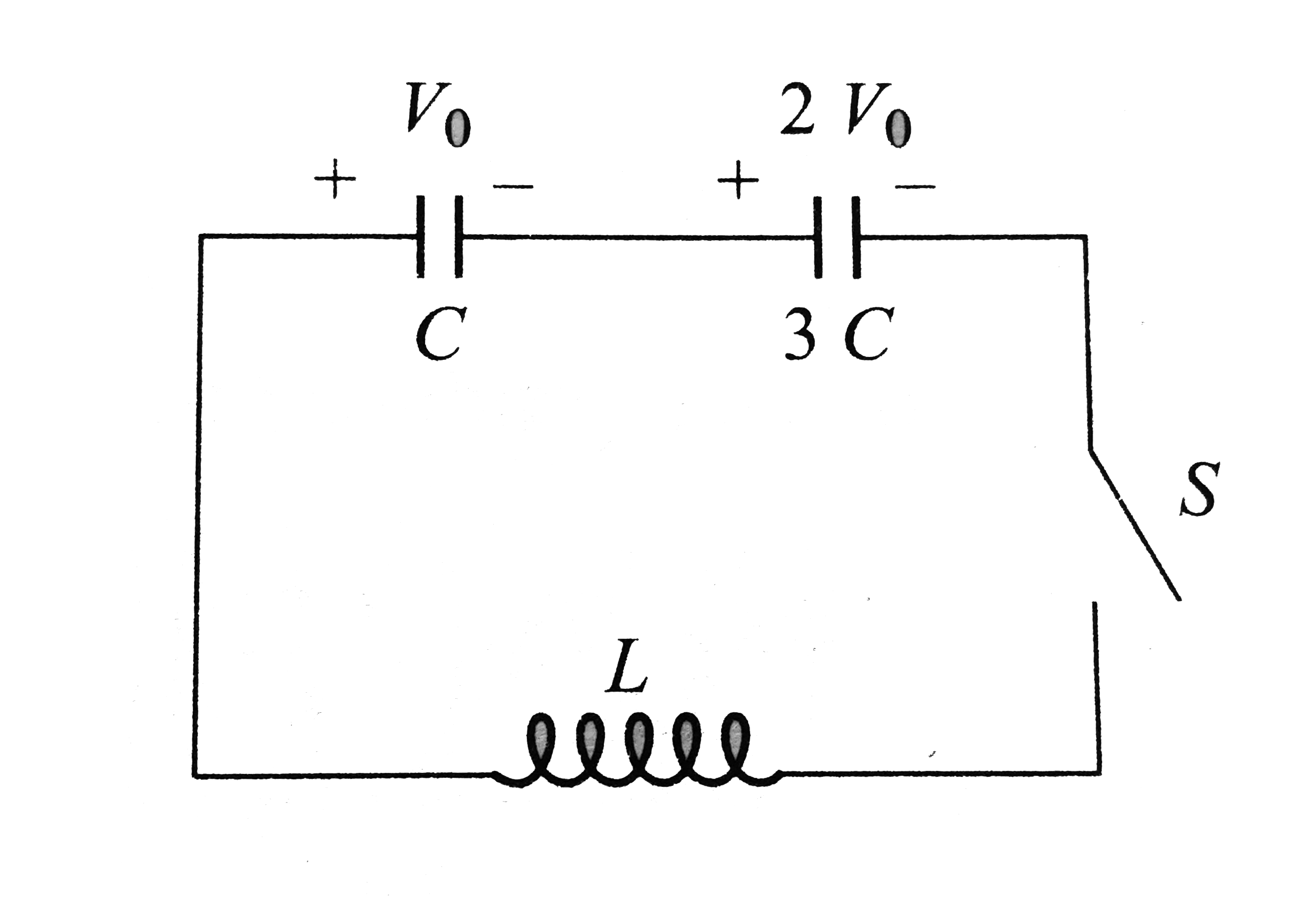
The maximum current in the inductor is
View SolutionThree capacitors of capacitance C1=3μf,C2=6μfandC3=10μf, are connected to a 10V battery as shown in Figure 3 below
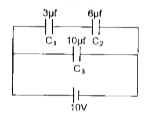
Calculate:
Equivalent capacitance
View SolutionTwo capacitors of capacitances 3μF and 6μF are charged to a potential of 12V each. They are now connected to each other, with the positive plate of each joined to the negative plate of the other. The potential difference across each will be
View Solution
