Two coils connected as shown in Fig. 30-48 separately have inductances L1 and L2. Their mutual inductance is M. (a) Show that this combination can be replaced by a single coil of equivalent inductance given by
Leq=L1+L2+2M
(b) How could the coils in Fig. 30-48 be reconnected to yield an equivalent inductance of
Leq=L1+L2−2M?
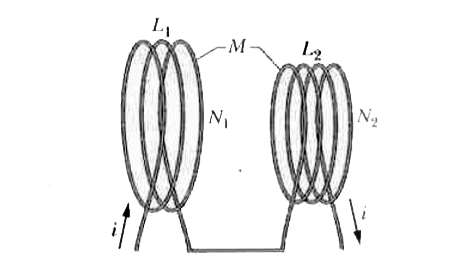
(b) have the turns of the two solenoids wrapped in opposite directions, Leq=L1+L2−2M
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - PRACTICE QUESTIONS (Single Correct Choice Type)
45 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - PRACTICE QUESTIONS (More than One Correct Choice Type)
13 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - CHECKPOINTS
9 Videos
- ELECTRIC POTENTIALBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - (PRACTICE QUESTIONS) Integer Type
1 Videos
- ELECTROMAGNETIC OSCILLATIONS AND ALTERNATING CURRENT BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTROMAGNETIC OSCILLATIONS AND ALTERNATING CURRENT EXERCISE - Practice Questions (Integer)
7 Videos
Similar Questions
In Fig. coil 1 and coil 2 are wound on a long cylindrical insulator. The ends A' and B are joined together and current I is passed. Self-inductance of the two coils are L1 and L2, and their mutual inductance is M.
a. Show that this combination can be replaced by a single coil of equivalent inductange given by
Leq=L1+L2+2M.
b. How could the coils be reconnected by yieldings an equivalent inductance of Leq=L1+L2−2M.

View SolutionIn Fig. coil 1 and coil 2 are wound on a long cylindrical insulator. The ends A' and B are joined together and current I is passed. Self-inductance of the two coils are L1 and L2, and their mutual inductance is M.
a. Show that this combination can be replaced by a single coil of equivalent inductange given by
Leq=L1+L2+2M.
b. How could the coils be reconnected by yieldings an equivalent inductance of Leq=L1+L2−2M.

View Solution
Knowledge Check
The inductors of self inductance L1 and L2 are put in series .
AL1+L2onlyBL1−L2onlyCMay be in between L1−L2 and L1+L2DL1+2L2Coefficient of coupling between two coils of self-inductances L1 and L2 is unity. It means
A50% of L1 is linked with L2B√L1 time of L1 is linked with L2C100% of L1 is linked with L2Dnone of the aboveCoefficient of coupling between two coils of self-inductances L1 and L2 is unity. It means
A50% flux of L1 is linked with L2B100% flux of L1 is linked with L2C√L1 time of flux of L1 is linked with L2DNone of the above
The inductors of self inductance L1 and L2 are put in series .
View SolutionTwo inductances L1 & L2 are connected in series & are seperated by a large distance.
(a) Show that their equivalent inductance is L1+L2.
(b) Why must their seperation be larger ?
View SolutionTwo inductances L1 & L2 are connected in series & are seperated by a large distance.
(a) Show that their equivalent inductance is L1+L2.
(b) Why must their seperation be larger ?
View SolutionCoefficient of coupling between two coils of self-inductances L1 and L2 is unity. It means
View SolutionTwo coils of self inductance L_1 and L_2 are placed near each other so that the total flux in one coil is partially linked with the other. Their mutual inductance (M) will be given by
View Solution
